Chapter 10 – Division of Polynomials
Practice set 10.1
1. Divide. Write the quotient and the remainder.
(1) 21m² ÷ 7m
Solution:
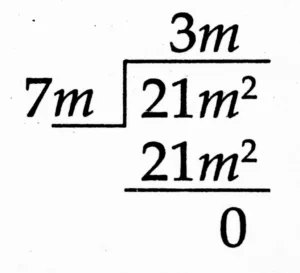
Quotient: 7m
Remainder: 0
(2) 40a³ ÷ (– 10a)
Solution:
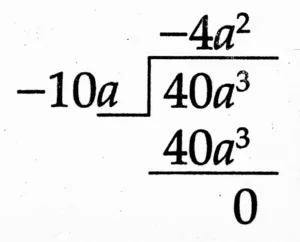
Quotient: – 4a²
Remainder: 0
(3) (– 48p⁴) ÷ (– 9p²)
Solution:
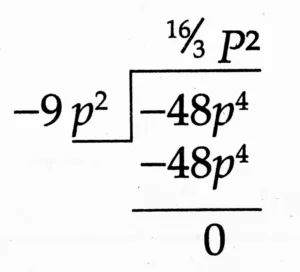
Quotient: \(\large \frac {16}{3}\)p²
Remainder: 0
(4) 40m⁵ ÷ 30m⁵
Solution:
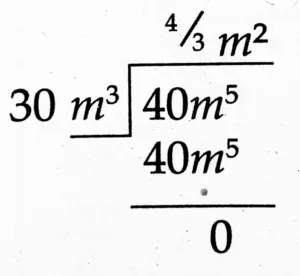
Quotient: \(\large \frac {4}{3}\)m²
Remainder: 0
(5) (5x³ – 3x²) ÷ x²
Solution:
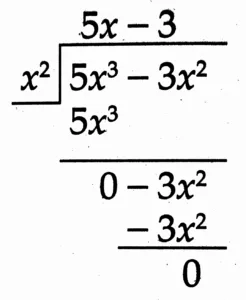
Quotient: 5x – 3
Remainder: 0
(6) (8p³ – 4p²) ÷ 2p²
Solution:
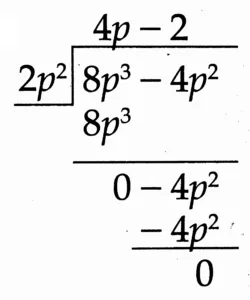
Quotient: 4p – 2
Remainder: 0
(7) (2y³ + 4y² + 3) ÷ 2y²
Solution:
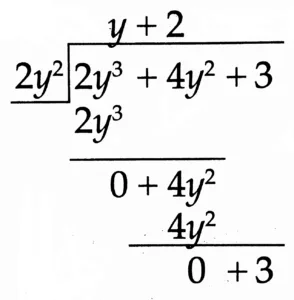
Quotient: y + 2
Remainder: 3
(8) (21x⁴ – 14x² + 7x) ÷ 7x³
Solution:
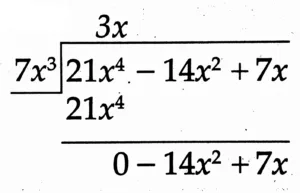
Quotient: 3x
Remainder: – 14x² + 7x
(9) (6x⁵ – 4x⁴ + 8x³ + 2x²) ÷ 2x²
Solution:
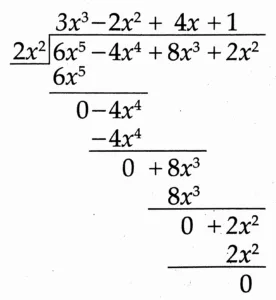
Quotient: 3x³ – 2x² + 4x + 1
Remainder: 0
(10) (25m⁴ – 15m³ + 10m + 8) ÷ 5m³
Solution:

Quotient: 5m – 3
Remainder: 10m + 8
Practice set 10.2
1. Divide and write the quotient and the remainder.
(1) (y² + 10y + 24) ÷ (y + 4)
Solution:
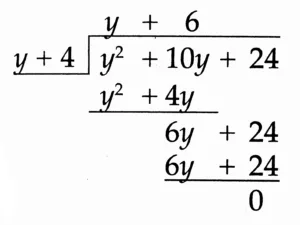
Quotient: y + 6
Remainder: 0
(2) (p² + 7p – 5) ÷ (p + 3)
Solution:
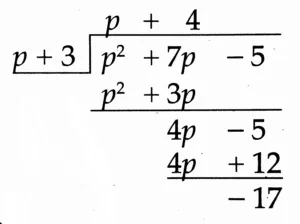
Quotient: p + 3
Remainder: – 17
(3) (3x + 2x² + 4x³) ÷ (x – 4)
Solution:
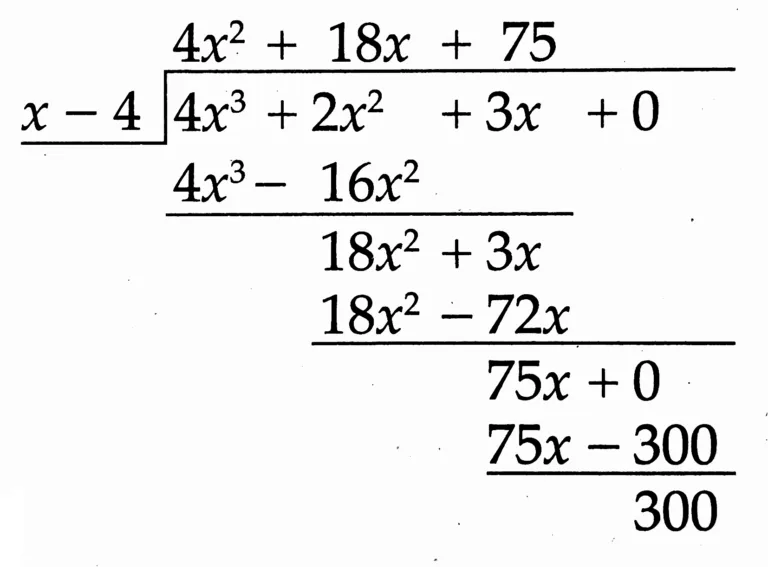
Quotient: 4x² + 18x + 75
Remainder: 300
(4) (2m³ + m² + m + 9) ÷ (2m – 1)
Solution:
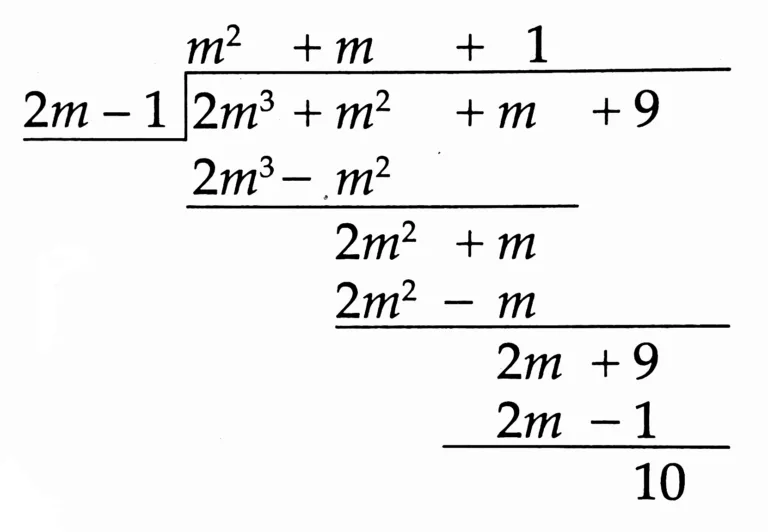
Quotient: m² + m + 1
Remainder: 10
(5) (3x – 3x² – 12 + x⁴ + x³) ÷ (2 + x²)
Solution:
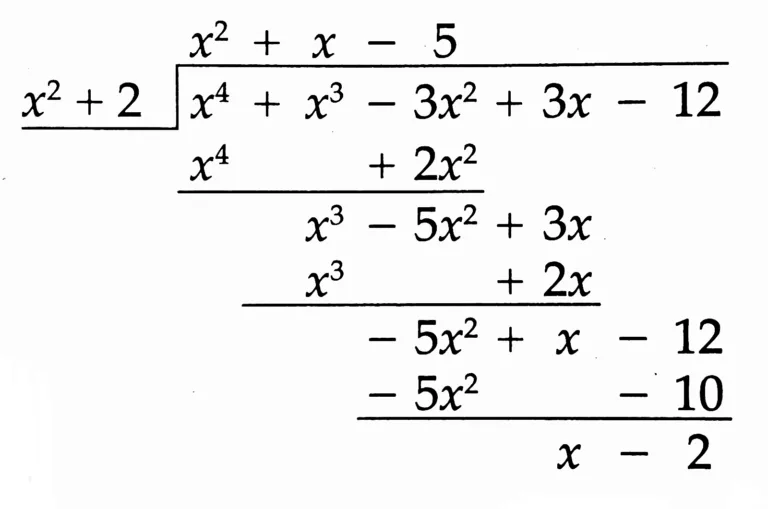
Quotient: x² + x – 5
Remainder: x – 2
(6*) (a⁴ – a³ + a² – a + 1) ÷ (a³ – 2)
Solution:
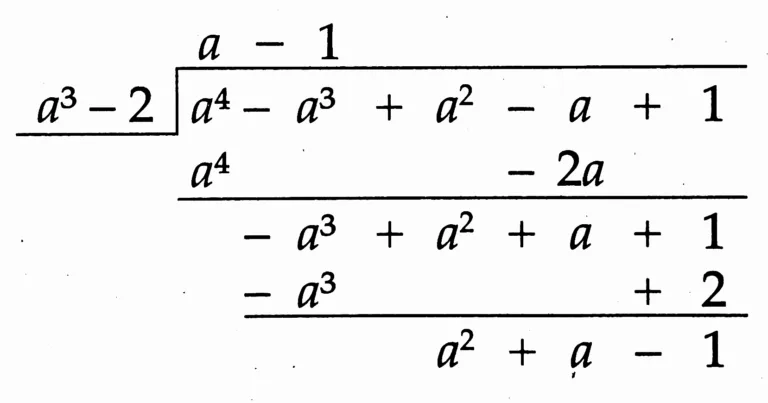
Quotient: a – 1
Remainder: a² + a – 1
(7*) (4x⁴ – 5x³ – 7x + 1) ÷ (4x – 1)
Solution:
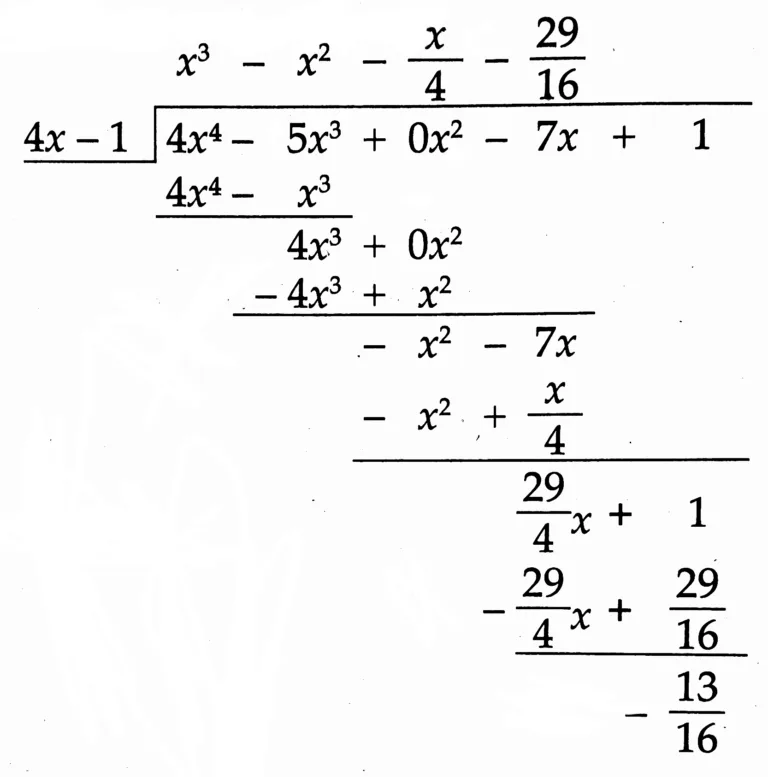
Quotient: x³ – x² – \(\large \frac {x}{4}\) – \(\large \frac {29}{16}\)
Remainder: – \(\large \frac {13}{16}\)
