Miscellaneous Exercise 1
1. Choose the correct alternative answer for each of the following questions.
(1) In ▯PQRS, m∠P = m∠R = 108°, m∠Q = m∠S = 72°. State which pair of sides of those given below is parallel.
(A) Side PQ and side QR
(B) side PQ and side SR
(C) side SR and side SP
(D) side PS and side PQ
Ans: Option (B) – side PQ and side SR

Solution:
In □ PQRS,
m∠P + m∠S
= 108°+ 72
= 180°
Since, interior angles are supplementary
∴ side PQ || side SR
(2) Read the following statements and choose the correct alternative from those given below them.
(i) Diagonals of a rectangle are perpendicular bisectors of each other.
(ii) Diagonals of a rhombus are perpendicular bisectors of each other.
(iii) Diagonals of a parallelogram are perpendicular bisectors of each other.
(iv) Diagonals of a kite bisect each other.
(A) Statement (ii) and (iii) are true
(B) Only statement (ii) is true
(C) Statements (ii) and (iv) are true
(D) Statements (i), (iii) and (iv) are true.
Ans: Option (B) – Only statement (b) is true
(3) If 19³ = 6859, find \(\sqrt[3]{0.006859}\)
(A) 1.9
(B) 19
(C) 0.019
(D) 0.19
Ans: Option (D) – 0.19
Solution:
\(\sqrt[3]{0.006859}\)
= \(\sqrt[3]{\large \frac {6859}{1000000}}\)
= \(\large \frac {\sqrt[3]{6859}}{\sqrt[3]{1000000}}\)
= \(\large \frac {\sqrt[3]{19³}}{\sqrt[3]{100³}}\)
= \(\large \frac {19}{100}\)
= 0.19
2. Find the cube roots of the following numbers.
(1) 5832
Solution:
5832
= 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
= (2 × 3 × 3) × (2 × 3 × 3) × (2 × 3 × 3)
= (2 × 3 × 3)³
= (18)³
∴ \(\sqrt[3]{5832}\) = 18
(2) 4096
Solution:
4096
= (4 × 4) × (4 × 4) × (4 × 4)
= (4 × 4)
= 16³
∴ \(\sqrt[3]{4096}\) = 16
3. m α n, n = 15 when m = 25. Hence
(1) Find m when n = 87
(2) Find n when m = 155
Given:
m α n
∴ m = kn …(i) [k is the constant of variation]
When m = 25, n = 15
∴ Substituting, m = 25 and n = 15 in (i), we get,
m = kn
∴ 25 = k × 15
∴ k = \(\large \frac {25}{215}\)
∴ k = \(\large \frac {5}{3}\)
Substituting k = \(\large \frac {5}{3}\) in (i), we get,
m = kn
∴ m = \(\large \frac {5}{3}\)n …(ii)
(1) When n = 87, m = ?
Substituting n = 87 in (ii), we get
m = \(\large \frac {5}{3}\) n
m = \(\large \frac {5}{3}\) × 87
m = 5 × 29
m = 145
(2) When m = 155, n = ?
Substituting m = 155 in (ii), we get
m = \(\large \frac {5}{3}\) n
∴ 155 = \(\large \frac {5}{3}\) n
∴ 155 × \(\large \frac {3}{5}\) = n
∴ n = 31 × 3
∴ n = 93
4. y varies inversely with x. If y = 30 when x = 12, find
(1) y when x = 15
(2) x when y = 18
Solution:
y α \(\large \frac {1}{x}\)
∴ y = k × \(\large \frac {1}{x}\) [where, k is the constant of variation]
∴ y × x = k …(i)
When x = 12, y = 30
∴ Substituting, x = 12 and y = 30 in (i), we get,
y × x = k
∴ 30 × 12 = k
∴ k = 360
Substituting, k = 360 in (i), we get
y × x = k
∴ y × x = 360 …(ii)
(1) When x = 15, y = ?
∴ Substituting x = 15 in (ii), we get
y × x = 360
∴ y × 15 = 360
∴ y = \(\large \frac {360}{15}\)
∴ y = 24
(2) When y = 18, x = ?
∴ Substituting y = 18 in (ii), we get
y × x = 360
∴18 × x = 360
∴ x = \(\large \frac {360}{18}\)
∴ x = 20
5. Draw a line l. Draw a line parallel to line l at a distance of 3.5 cm.
Solution:

6. Fill in the blanks in the following statement.
The number \((256)^{\large \frac {5}{7}}\) is ____ th root of ____ th power of ____.
Ans: The number \((256)^{\large \frac {5}{7}}\) is 7 th root of 5 th power of 256.
7. Expand.
(1) (5x – 7) (5x – 9)
Solution:
(5x – 7) (5x – 9)
= (5x)² + (– 7 – 9) 5x + (– 7) × (– 9) …[∵ (x + a) (x + b) = x² + (a + b)x + ab]
= 25x² + (– 16) × 5x + 63
= 25x² – 80x + 63
(2) (2x – 3y)³
Solution:
Here,
a = 2x and b = 3y
∴ (2x – 3y)³
= (2x)³ – 3 (2x)² (3y) + 3 (2x) (3y)² – (3y)³ …[∵ (a – b)³ = a³ – 3a²b + 3ab² – b³]
= 8x³ – 3 (4x²) (3y) + 3 (2x) (9y²) – 27y³
= 8x³ – 36x²y + 54xy² – 27p³
(3) \(\large (\)a + \(\large \frac {1}{2})^{3}\)
Solution:
Here,
A = a
B = \(\large \frac {1}{2}\)
∴ \(\large (\)a + \(\large \frac {1}{2})^{3}\)
= (a)³ + 3(a)²\(\large (\frac {1}{2})\) + 3(a)\(\large (\frac {1}{2})^{2}\) + \(\large (\frac {1}{2})^{3}\) …[(A + B)³ = A³ + 3A²B + 3AB² + B³]
= a³ + \(\large (\frac {3a²}{2})\) + 3(a)\(\large (\frac {1}{4})\) + \(\large \frac {1}{8}\)
= a³ + \(\large \frac {3a²}{2}\) + \(\large \frac {3a}{4}\) + \(\large \frac {1}{8}\)
8. Draw an obtuse angled triangle. Draw all of its medians and show their point of concurrence.
Solution:
P, Q and R are the mid-points of sides TV, SV and ST respectively.
Hence, Seg SP, Seg TQ and VR are the medians. They are concurrent. Point of concurrence is G.

9. Draw ∆ABC such that l (BC) = 5.5 cm, m∠ABC = 90°, l (AB) = 4 cm. Show the orthocentre of the triangle.
Solution:

Vertex B is the orthocentre of ∆ABC.
10. Identify the variation and solve. It takes 5 hours to travel from one town to the other if the speed of the bus is 48 km/hr. If the speed of the bus is reduced by 8 km/hr, how much time will it take for the same travel ?
Solution:
Let us assume the speed of the vehicle to be s and time taken to travel be t.
s α \(\large \frac {1}{t}\)
∴ st = k …[where k is the constant of variation]
∴ k = s × t
∴ k = 48 × 5
∴ k = 240
Now ,
The value of t when s = (48 – 8) = 40 km/hr is,
s × t = 240
∴ 40 × t = 240
∴ t = \(\large \frac {240}{6}\)
∴ t = 6
Ans: Time taken to travel the same distance at the speed 40 km/hr is 6 hours.
11. Seg AD and seg BE are medians of ∆ABC and point G is the centroid. If l(AG) = 5 cm, find l(GD). If l(GE) = 2 cm, find l(BE).
Solution:
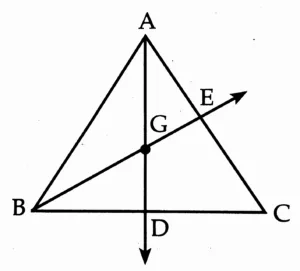
Centroid G divides the median in the ratio 2 : 1
(i) Point G is the centroid and seg AD is the median.
\(\large \frac {AG}{GD}\) = \(\large \frac {2}{1}\)
∴ \(\large \frac {5}{GD}\) = \(\large \frac {2}{1}\)
∴ 5 = 2 × l(GD)
∴ l(GD) = \(\large \frac {5}{2}\)
∴ l(GD) = 2.5 cm
(ii) Point G is the centroid and seg BE is the median
\(\large \frac {BG}{GE}\) = \(\large \frac {2}{1}\)
∴ \(\large \frac {BG}{2}\) = \(\large \frac {2}{1}\)
∴ l(BG) = 2 × 2
∴ l(BG) = 4
Now,
l(BE) = l(BG) + l(GE)
∴ l(BE) = 4 + 2
∴ l(BE) = 6 cm
12. Convert the following rational numbers into decimal form.
(1) \(\large \frac {8}{13}\)
Solution:

∴ \(\large \frac {8}{13}\) = \(0.\overline{615384}\)
(2) \(\large \frac {11}{7}\)
Solution:

∴ \(\large \frac {11}{7}\) = \(1.\overline{571428}\)
(3) \(\large \frac {5}{16}\)
Solution:

∴ \(\large \frac {5}{16}\) = 0.3125
(4) \(\large \frac {7}{9}\)
Solution:

∴ \(\large \frac {7}{9}\) = \(0.\dot{7}\)
13. Factorise.
(1) 2y² – 11y + 5
Solution:
2y² – 11y + 5
= 2y² – 10y – y + 5
= 2y(y – 5) – 1(y – 5)
= (y – 5)(2y – 1)
∴ 2y² – 11y + 5 = (y – 5)(2y – 1)
(2) x² – 2x – 80
Solution:
x² – 2x – 80
= x² – 10x + 8x – 80
= x (x – 10) + 8 (x – 10)
= (x – 10)(x + 8)
∴ x² – 2x – 80 = (x – 10)(x + 8)
(3) 3x² – 4x + 1
Solution:
3x² – 4x + 1
= 3x² – 3x – x + 1
= 3x(x – 1) – 1(x – 1)
= (x – 1) (3x – 1)
∴ 3x² – 4x + 1 = (x – 1) (3x – 1)
14. The marked price of a T. V. Set is ₹ 50000. The shopkeeper sold it at 15% discount. Find the price of it for the customer.
Solution:
Marked price = Rs 50,000,
Discount = 15%
Let the discount percent be x
∴ x = 15%
We know that,
Discount = \(\large \frac {Marked\, Price\,×\,x}{100}\)
∴ Discount = \(\large \frac {50000\,×\,15}{100}\)
∴ Discount = 500 × 15
∴ Discount = ₹ 7500
Now,
Selling price = Marked price – Discount
∴ Selling price = 50000 – 7500
∴ Selling price = Rs 42500
Ans: The price of the T.V. set for the customer is Rs 42,500.
15. Rajabhau sold his flat to Vasantrao for ₹ 88,00,000 through an agent. The agent charged 2 % commission for both of them. Find how much commission the agent got.
Solution:
Selling price of the flat = Rs 88,00,000
Rate of commission = 2%
∴ Commission
= 2% of selling price
= \(\large \frac {2}{100}\) × 88,00,000
= 2 × 88,000
= Rs 1,76,000
∴ Total commission
= Commission from Rajabhau + Commission from Vasantrao
= 1,76,000 + 1,76,000
= Rs 3,52,000
Ans: The agent got a commission of Rs 3,52,000.
16. Draw a parallelogram ABCD. such that l(DC) = 5.5 cm, m∠D = 45°, l(AD) = 4 cm.
Solution:
Opposite sides of a parallelogram are congruent.
∴ l(AB) = l(DC) = 5.5 cm and l(AD) = l(BC) = 4 cm
Opposite angles of a parallelogram are congruent.
∴ m∠D = m∠B = 45⁰
Adjacent angles are of a parallelogram supplementary
∴ m∠A + m∠D = 180⁰
∴ m∠A = 180⁰ – m∠D
∴ m∠A = 180 – 45⁰
∴ m∠C = m∠A = 135⁰
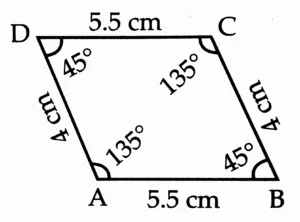
Rough Figure

This is the required construction.
17. In the figure, line l || line m and line p || line q. Find the measures of ∠a , ∠b, ∠c and ∠d.

Solution:
line l || line m and line p is a transversal.
∴ m∠a = 78° …(i) [Corresponding angles]
line p || line q and line m is a transversal.
∴ m∠d = m∠a …[Corresponding angles]
∴ m∠d = 78° …(ii) [From (i)]
m∠b = m∠d …[Vertically opposite angles]
∴ m∠b = 78° …[From (ii)]
line l || line m and line q is a transversal.
∴ m∠c + m∠d = 180° …[Interior angles]
∴ m∠c + 78° = 180° …[From (ii)]
∴ m∠c =180° – 78°
∴ m∠c = 102°
Ans: The measure of m∠a is 78°, m∠b is 78°, m∠c is 102° and m∠d is 78°
