Miscellaneous Problems : Set 1
1. Solve the following.
(i) (– 16) × (– 5)
Solution:
(– 16) × (– 5) = 80
(ii) (72) ÷ (– 12)
Solution:
72 ÷ (– 12) = \(\large \frac {72}{(–\,1)\,×\,12}\)
∴ 72 ÷ (– 12) = \(\large \frac {12\,×\,6}{(–\,1)\,×\,12}\)
∴ 72 ÷ (– 12) = \(\large \frac {6}{(–\,1)}\)
∴ 72 ÷ (– 12) = – 6
(iii) (– 24) × (2)
Solution:
(– 24) × (2) = – 48
(iv) 125 ÷ 5
Solution:
125 ÷ 5 = \(\large \frac {25\,×\,5}{5}\)
∴ 125 ÷ 5 = 25
(v) (– 104) ÷ (– 13)
Solution:
(– 104) ÷ (– 13) = \(\large \frac {(–\,1)\,×\,104}{(–\,1)\,×\,13}\)
∴ (– 104) ÷ (– 13) = \(\large \frac {13\,×\,8}{13}\)
∴ (– 104) ÷ (– 13) = 8
(vi) 25 × (– 4)
Solution:
25 × (– 4) = – 100
2. Find the prime factors of the following numbers and find their LCM and HCF.
(i) 75, 135
Solution:

75 = 3 × 5 × 5
135 = 3 × 3 × 3 × 5
∴ HCF of 75 and 135 = 3 × 5
∴ HCF of 75 and 135 = 15
And,
LCM of 75 and 135 = 3 × 5 × 5 × 3 × 3
∴ LCM of 75 and 135 = 675
(ii) 114, 76
Solution:
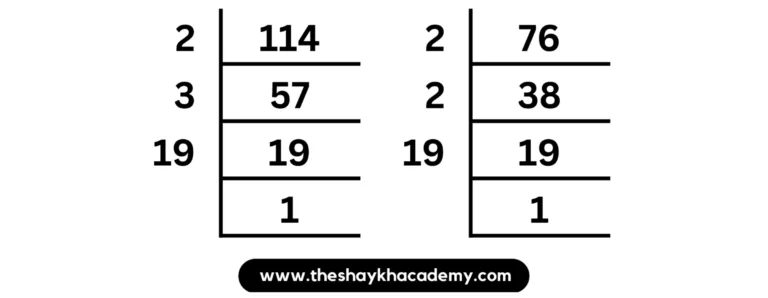
114 = 2 × 3 × 19
76 = 2 × 2 × 19
∴ HCF of 114 and 76 = 2 × 19
∴ HCF of 114 and 76 = 38
And,
LCM of 114 and 76 = 2 × 19 × 3 × 2
∴ LCM of 114 and 76 = 228
(iii) 153, 187
Solution:
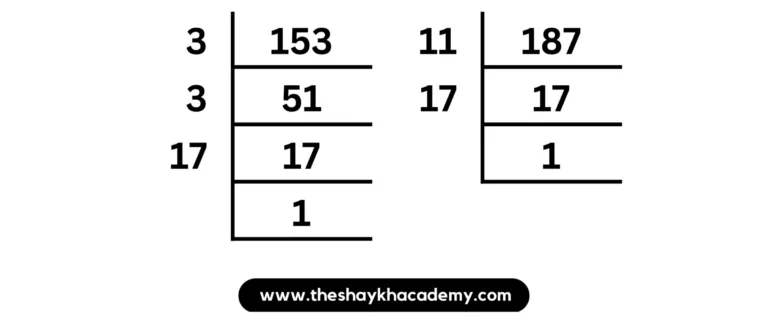
153 = 3 × 3 × 17
187 = 11 × 17
∴ HCF of 153 and 187 = 3 × 5
And,
LCM of 153 and 187 = 17 × 3 × 3 × 11
∴ LCM of 153 and 187 = 1683
(iv) 32, 24, 48
Solution:
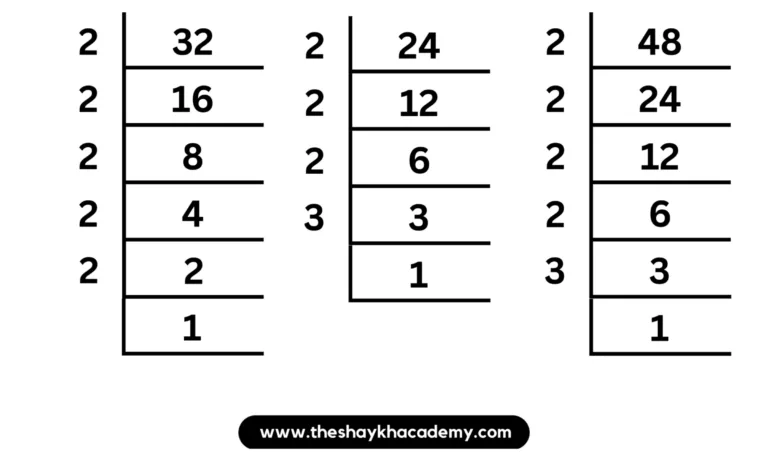
32 = 2 × 2 × 2 × 2 × 2
24 = 2 × 2 × 2 × 3
48 = 2 × 2 × 2 × 2 × 3
∴ HCF of 32, 24 and 48 = 2 × 2 × 2
∴ HCF of 32, 24 and 48 = 8
And,
LCM of 32, 24 and 48 = 2 × 2 × 2 × 2 × 2 × 3
∴ LCM of 32, 24 and 48 = 96
3. Simplify.
(i) \(\large \frac {322}{391}\)
Solution:
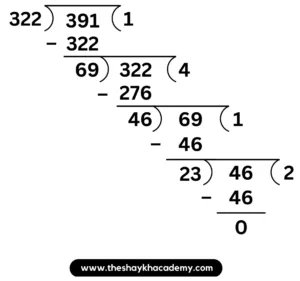
HCF of 322 and 391 = 23
∴ \(\large \frac {322}{391}\) = \(\large \frac {322\,÷\,23}{391\,÷\,23}\) = \(\large \frac {14}{17}\)
(ii) \(\large \frac {247}{209}\)
Solution:
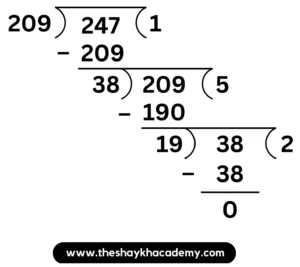
HCF of 247and 209 = 19
∴ \(\large \frac {247}{209}\) = \(\large \frac {247\,÷\,19}{209\,÷\,19}\) = \(\large \frac {13}{11}\)
(iii) \(\large \frac {117}{156}\)
Solution:
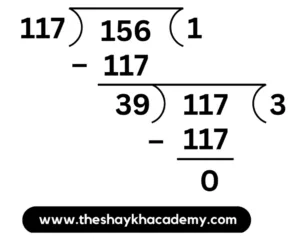
HCF of 117 and 156 = 39
∴ \(\large \frac {117}{156}\) = \(\large \frac {117\,÷\,39}{156\,÷\,39}\) = \(\large \frac {3}{4}\)
4. Find the square root of the following numbers.
(i) 784
Solution:

∴ 784 = 2 × 2 × 2 × 2 × 7 × 7
∴ \(\sqrt{784}\) = 2 × 2 × 7
∴ \(\sqrt{784}\) = 28
(ii) 225
Solution:

∴ 225 = 3 × 3 × 5 × 5
∴ \(\sqrt{225}\) = 3 × 5
∴ \(\sqrt{225}\) = 15
(iii) 1296
Solution:

∴ 1296 = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3
∴ \(\sqrt{1296}\) = 2 × 2 × 3 × 3
∴ \(\sqrt{1296}\) = 36
(iv) 2025
Solution:

∴ 2025 = 3 × 3 × 3 × 3 × 5 × 5
∴ \(\sqrt{2025}\) = 3 × 3 × 5
∴ \(\sqrt{2025}\) = 45
(v) 256
Solution:

∴ 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
∴ \(\sqrt{256}\) = 2 × 2 × 2 × 2
∴ \(\sqrt{256}\) = 16
5. There are four polling booths for a certain election. The numbers of men and women who cast their vote at each booth is given in the table below. Draw a joint bar graph for this data.

Solution:
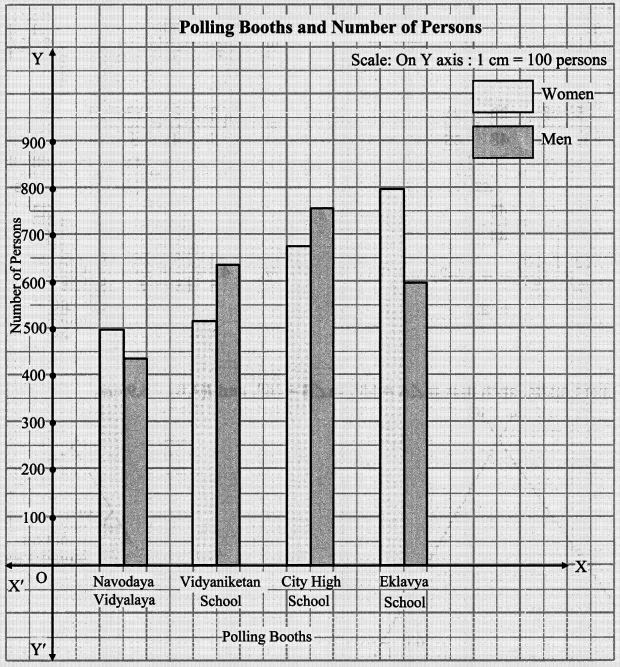
6. Simplify the expressions.
(i) 45 ÷ 5 + 20 × 4 – 12
Solution:
45 ÷ 5 + 120 × 4 – 12
= 9 + 80 – 12
= 89 – 12
= 77
∴ 45 ÷ 5 + 20 × 4 – 12 = 77
(ii) (38 – 8) × 2 ÷ 5 + 13
Solution:
(38 – 8) × 2 ÷ 5 + 13
= 30 × 2 ÷ 5 + 13
= 60 ÷ 5 + 13
= 12 + 13
= 25
∴ (38 – 8) × 2 ÷ 5 + 13 = 25
(iii) \(\large \frac {5}{3}\) + \(\large \frac {4}{7}\) ÷ \(\large \frac {32}{21}\)
Solution:
\(\large \frac {5}{3}\) + \(\large \frac {4}{7}\) ÷ \(\large \frac {32}{21}\)
= \(\large \frac {5}{3}\) + \(\large \frac {4}{7}\) × \(\large \frac {21}{32}\)
= \(\large \frac {5}{3}\) + \(\large \frac {3}{8}\)
= \(\large \frac {5\,×\,8}{3\,×\,8}\) + \(\large \frac {3\,×\,3}{8\,×\,3}\)
= \(\large \frac {40}{24}\) + \(\large \frac {9}{24}\)
= \(\large \frac {40\,+\,9}{24}\)
= \(\large \frac {49}{24}\)
∴ \(\large \frac {5}{3}\) + \(\large \frac {4}{7}\) ÷ \(\large \frac {32}{31}\) = \(\large \frac {49}{24}\)
(iv) 3 × {4 [85 + 5 – (15 ÷ 3)] + 2}
Solution:
3 × {4 [85 + 5 – (15 – 3)] + 2}
= 3 × {4[90 – 5] + 2}
= 3 × {4 × 85 + 2}
= 3 × (340 + 2)
= 3 × 342
= 1026
∴ 3 × {4 [85 + 5 – (15 ÷ 3)] + 2} = 1026
7. Solve.
(i) \(\large \frac {5}{12}\) + \(\large \frac {7}{16}\)
Solution:
\(\large \frac {5}{12}\) + \(\large \frac {7}{16}\)
= \(\large \frac {5\,×\,4}{12\,×\,4}\) + \(\large \frac {7\,×\,3}{16\,×\,3}\)
= \(\large \frac {20}{48}\) + \(\large \frac {21}{48}\)
= \(\large \frac{20 \,+\, 21}{48}\)
= \(\large \frac {41}{48}\)
∴ \(\large \frac {5}{12}\) + \(\large \frac {7}{16}\) = \(\large \frac {41}{48}\)
(ii) 3 \(\large \frac {2}{5}\) – 2 \(\large \frac {1}{4}\)
Solution:
3 \(\large \frac {2}{5}\) – 2 \(\large \frac {1}{4}\)
= \(\large \frac {3\,×\,5\,+\,2}{5}\) – \(\large \frac {2\,×\,4\,+\,1}{4}\)
= \(\large \frac {17}{5}\) – \(\large \frac {9}{4}\)
= \(\large \frac {17\,×\,4}{5\,×\,4}\) – \(\large \frac {9\,×\,5}{4\,×\,5}\)
= \(\large \frac {68}{20}\) – \(\large \frac {45}{20}\)
= \(\large \frac {68\,–\,45}{20}\)
= \(\large \frac {23}{20}\)
∴ 3 \(\large \frac {2}{5}\) – 2 \(\large \frac {1}{4}\) = \(\large \frac {23}{20}\)
(iii) \(\large \frac {12}{5}\) × \(\large \frac {–\,10}{3}\)
Solution:
\(\large \frac {12}{5}\) × \(\large \frac {–\,10}{3}\)
= 4 × (– 2)
= – 8
∴ \(\large \frac {12}{5}\) × \(\large \frac {–\,10}{3}\) = – 8
(iv*) 4 \(\large \frac {3}{8}\) ÷ \(\large \frac {25}{18}\)
Solution:
4 \(\large \frac {3}{8}\) ÷ \(\large \frac {25}{18}\)
= \(\large \frac {4\,×\,8\,+\,3}{8}\) ÷ \(\large \frac {25}{18}\)
= \(\large \frac {35}{8}\) ÷ \(\large \frac {25}{18}\)
= \(\large \frac {35}{8}\) × \(\large \frac {18}{25}\)
= \(\large \frac {7}{4}\) × \(\large \frac {9}{5}\)
= \(\large \frac {63}{20}\)
∴ 4 \(\large \frac {3}{8}\) ÷ \(\large \frac {25}{18}\) = \(\large \frac {63}{20}\)
8. Construct ∆ABC such that m∠A = 55°, m∠B = 60°, and l(AB) = 5.9 cm.
Solution:
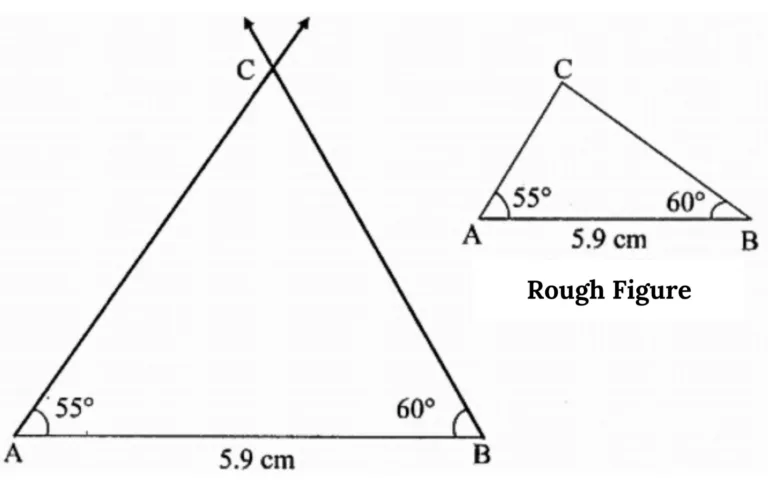
This is the required construction.
9. Construct ∆XYZ such that, l(XY) = 3.7 cm, l(YZ) = 7.7 cm, l(XZ) = 6.3 cm.
Solution:
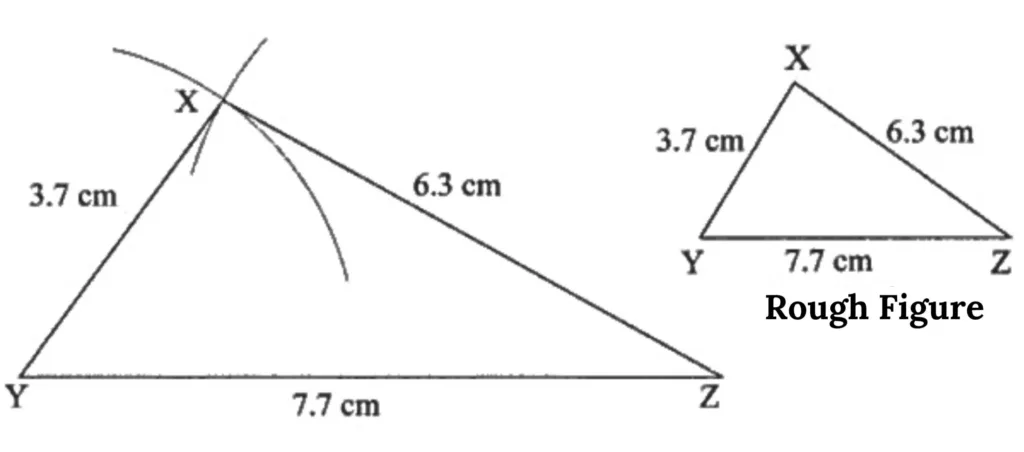
This is the required construction.
10. Construct ∆PQR such that, m∠P = 80°, m∠Q = 70°, l(QR) = 5.7 cm.
Solution:
In ∆PQR,
m∠P + m∠Q + m∠R = 180° …[Sum of the measures of the angles of a triangle is 180°]
∴ 80 + 70 + m∠R = 180
∴ 150 + m∠R = 180
∴ m∠R = 180 – 150
∴ m∠R = 30°
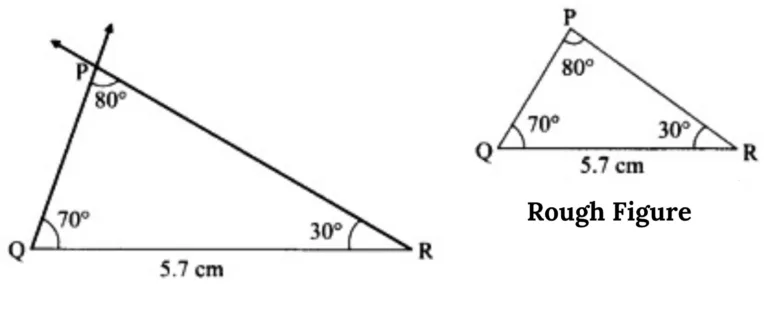
This is the required construction.
11. Construct ∆EFG from the given measures. l(FG) = 5 cm, m∠EFG = 90°, l(EG) = 7 cm.
Solution:
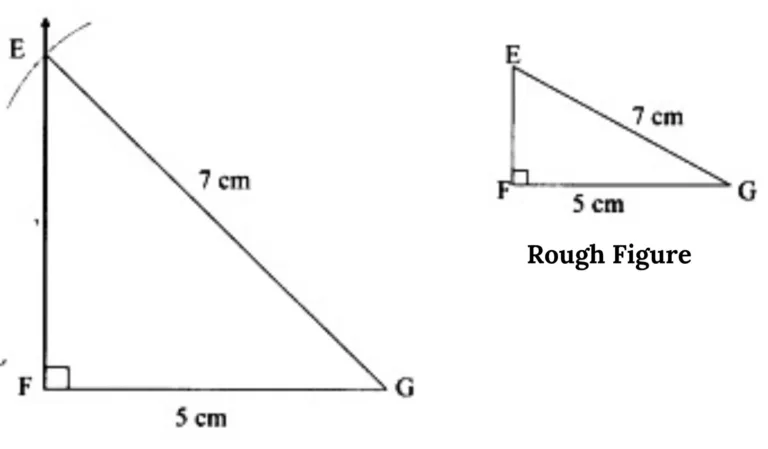
This is the required construction.
12. In ∆LMN, l(LM) = 6.2 cm, m∠LMN = 60°, l(MN) = 4 cm. Construct ∆LMN.
Solution:
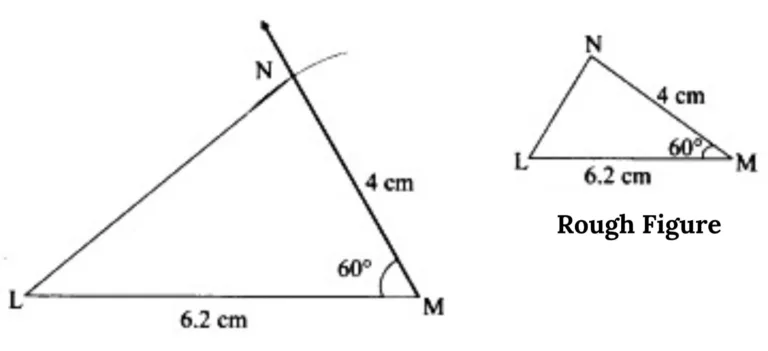
This is the required construction.
13. Find the measures of the complementary angles of the following angles.
(i) 35°
Solution:
Let the measure of the complementary angle be x°.
35 + x = 90
∴ x = 90 – 35
∴ x = 55
∴ The complementary angle of 35° is 55°.
(ii) a°
Solution:
Let the measure of the complementary angle be x°.
a + x = 90
∴ x = 90 – a
∴ The complementary angle of a° is (90 – a)°.
(iii) 22°
Solution:
Let the measure of the complementary angle be x°.
22 + x = 90
∴ x = 90 – 22
∴ x = 68
∴ The complementary angle of 22° is 68°.
(iv) (40 – x)°
Solution:
Let the measure of the complementary angle be a°.
40 – x + a = 90
∴ a = 90 – 40 + x
∴ a = 50 + x
∴ The complementary angle of (40 – x)° is (50 + x)°.
14. Find the measures of the supplements of the following angles.
(i) 111°
Solution:
Let the measure of the supplementary
angle be x°.
111 + x = 180
∴ x = 180 – 111
∴ x = 69
∴ The supplementary angle of 111° is 69°.
(ii) 47°
Solution:
Let the measure of the supplementary angle be x°.
47 + x = 180
∴ x = 180 – 47
∴ x = 133
∴ The supplementary angle of 47° is 133°.
(iii) 180°
Solution:
Let the measure of the supplementary angle be x°.
180 + x = 180
∴ x = 180 – 180
∴ x = 0
∴ The supplementary angle of 180° is 0°.
(iv) (90 – x)°
Solution:
Let the measure of the supplementary angle be a°.
90 – x + a = 180
∴ a = 180 – 90 + x
∴ a = 90 + x
∴ The supplementary angle of (90 – x)° is (90 + x)°.
15. Construct the following figures.
(i) A pair of adjacent angles
Solution:
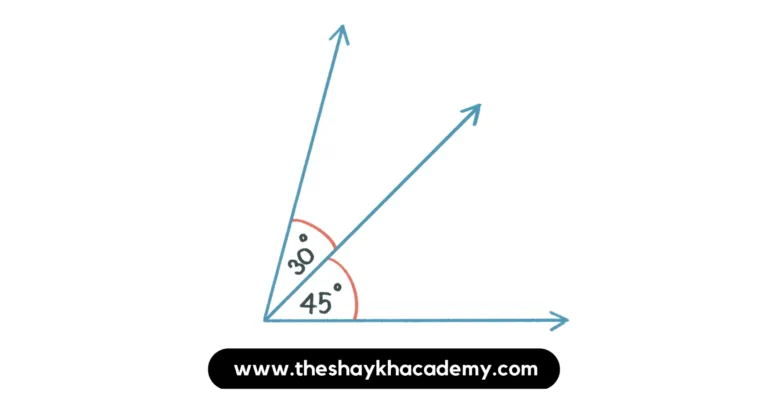
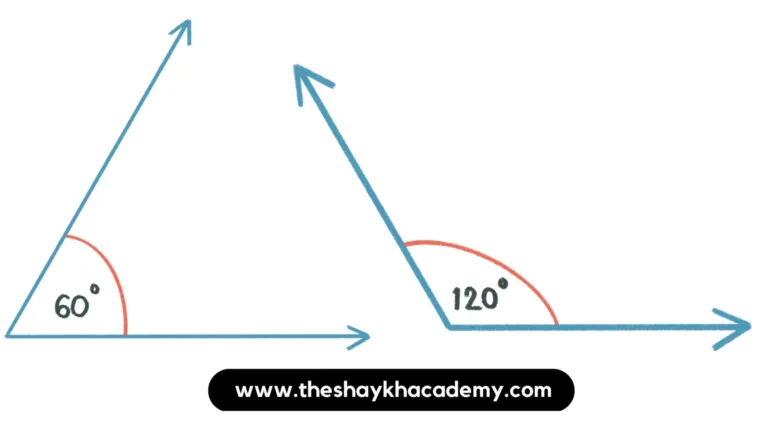
(ii) Two supplementary angles which are not adjacent angles.
Solution:
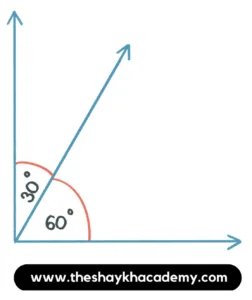
(iii) A pair of adjacent complementary angles.
Solution:
16. In ∆PQR, the measures of ∠P and ∠Q are equal and m∠PRQ = 70°. Find the measures of the following angles.
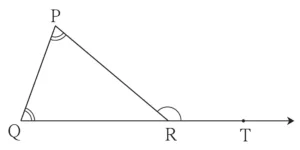
(i) m∠PRT
(ii) m∠P
(iii) m∠Q
Solution:
∠PRQ and ∠PRT are angles in a linear pair.
m∠PRQ + m∠PRT = 180°
∴ 70 + m∠PRT = 180
∴ m∠PRT = 180 – 70
∴ m∠PRT = 110°
Now,
∠PRT is the exterior angle of ∆PQR.
∴ m∠P + m∠Q = m∠PRT
∴ m∠P + m∠P = m∠PRT …[The measures of ∠P and ∠Q is same]
∴ 2m∠P = 110
∴ m∠P = \(\large \frac {110}{2}\)
∴ m∠P = 55°
and m∠Q = 55°
17. Simplify.
(i) 5⁴ × 5³
Solution:
5⁴ × 5³
= 5 ⁴+³
= 5⁷
∴ 5⁴ × 5³ = 5⁷
(ii) \(\left(\large\frac23\right)^6\) ÷ \(\left(\large\frac23\right)^9\)
Solution:
\(\left(\large\frac23\right)^6\) ÷ \(\left(\large\frac23\right)^9\)
= \(\left(\large\frac23\right)^{6\;-\;9}\)
= \(\left(\large\frac23\right)^{-3}\)
= \(\left(\large\frac32\right)^{3}\)
∴ \(\left(\large\frac23\right)^6\) ÷ \(\left(\large\frac23\right)^9\) = \(\left(\large\frac32\right)^{3}\)
(iii) \(\left (\large \frac72\right)^8\) × \(\left (\large \frac72\right)^{-6}\)
Solution:
\(\left (\large \frac72\right)^8\) × \(\left (\large \frac72\right)^{-6}\)
= \(\left (\large \frac72\right)^{8\,+(-6)}\)
= \(\left (\large \frac72\right)^{8-6}\)
= \(\left (\large \frac72\right)^2\)
∴ \(\left (\large \frac72\right)^8\) × \(\left (\large \frac72\right)^{-6}\) = \(\left (\large \frac72\right)^2\)
(iv) \(\left (\large \frac45\right)^2\) ÷ \(\left (\large \frac54\right)\)
Solution:
\(\left (\large \frac45\right)^2\) ÷ \(\left (\large \frac54\right)\)
= \(\left (\large \frac45\right)^2\) × \(\left (\large \frac45\right)\)
= \(\left (\large \frac45\right)^{2+1}\)
= \(\left (\large \frac45\right)^3\)
∴ \(\left (\large \frac45\right)^2\) ÷ \(\left (\large \frac54\right)\) = \(\left (\large \frac45\right)^3\)
18. Find the value.
(i) 17\(^{16}\) ÷ 17\(^{16}\)
Solution:
17\(^{16}\) ÷ 17\(^{16}\)
= 17\(^{16\, – \,16}\)
= 17\(^0\)
= 1
∴ 17\(^{16}\) ÷ 17\(^{16}\) = 1
(ii) 10\(^{-\,3}\)
Solution:
10\(^{-\,3}\)
= \(\large \frac{1}{10^3}\)
= \(\large \frac{1}{1000}\)
∴ 10\(^{-\,3}\) = \(\large \frac{1}{1000}\)
(iii) (23)\(^2\)
Solution:
(23)\(^2\)
= 23 × 23
= 529
∴ (23)\(^2\) = 529
(iv) 4\(^6\) × 4\(^{-\,4}\)
Solution:
4\(^6\) × 4\(^{-\,4}\)
= 4\(^{6\,+(-4)}\)
= 4\(^{6\,-\,4}\)
= 4\(^2\)
= 4 × 4
= 16
∴ 4\(^6\) × 4\(^{-\,4}\) = 16
19. Solve.
(i) (6a – 5b – 8c) + (15b + 2a – 5c)
Solution:
(6a – 5b – 8c) + (15b + 2a – 5c)
= (6a + 2a) + (– 5b + 15b) + (– 8c – 5c)
= 8a + 10b – 13c
∴ (6a – 5b – 8c) + (15b + 2a – 5c) = 8a + 10b – 13c
(ii) (3x + 2y)(7x – 8y)
Solution:
(3x + 2y) (7x – 8y)
= 3x × (7x – 8y) + 2yx (7x – 8y)
= 21x² – 24xy + 14xy – 16y²
= 21x² – 10xy – 16y²
∴ (3x + 2y) (7x – 8y) = 21x² – 10xy – 16y²
(iii) (7m – 5n) – (– 4n – 11m)
Solution:
(7m – 5n) – (– 4n – 11m)
= 7m – 5n + 4n + 11m
= (7m + 11m) + (– 5n + 4n)
= 18m – n
∴ (7m – 5n) – (– 4n – 11m) = 18m – n
(iv) (11m – 12n + 3p) – (9m + 7n – 8p)
Solution:
(11m – 12n + 3p) – (9m + 7n – 8p)
= 11m – 12n + 3p – 9m – 7n + 8p
= (11m – 9m) + (– 12n – 7n) + (3p + 8p)
= 2m – 19n + 11p
∴ (11m – 12n + 3p) – (9m + 7n – 8p) = 2m – 19n + 11p
20. Solve the following equations.
(i) 4(x + 12) = 8
Solution:
4(x + 12) = 8
∴ 4x + 48 = 8
∴ 4x = 8 – 48
∴ 4x = − 40
∴ x = − \(\large \frac {40}{4}\)
∴ x = − 10
(ii) 3y + 4 = 5y – 6
Solution:
3y + 4 = 5y – 6
∴ 3y + 4 + 6 = 5y
∴ 3y + 10 = 5y
∴ 10 = 5y – 3y
∴ 2y = 10
∴ y = \(\large \frac {10}{2}\)
∴ y = 5
Multiple Choice Questions
Choose the right answer from the options given after every question.
1. The three angle bisectors of a triangle are concurrent. Their point of concurrence is called the ______.
(i) circumcentre
(ii) apex
(iii) incentre
(iv) point of intersection
Ans: Option (iii) : incentre
2. \(\large [(\frac {3}{7})\small^{-3}\large] \small^{-4}\) = ______.
(i) \(\large (\frac {3}{7})\small^{-7}\)
(ii) \(\large (\frac {3}{7})\small^{-10}\)
(iii) \(\large (\frac {7}{3})\small^{12}\)
(iv) \(\large (\frac {3}{7})\small^{20}\)
Ans: Option (iii) : \(\large (\frac {7}{3})\small^{12}\)
3. The simplest form of 5 ÷ \(\large (\frac {3}{2})\) – \(\large \frac {1}{3}\) is ______.
(i) 3
(ii) 5
(iii) 0
(iv) \(\large \frac {1}{3}\)
Ans: Option (i) : 3
4. The solution of the equation 3x – \(\large \frac {1}{2}\) = \(\large \frac {5}{2}\) + x is ______
(i) \(\large \frac {5}{3}\)
(ii) \(\large \frac {7}{2}\)
(iii) 4
(iv) \(\large \frac {3}{2}\)
Ans: Option (iv) : \(\large \frac {3}{2}\)
5*. Which of the following expressions has the value 37?
(i) 10 × 3 + (5 + 2)
(ii) 10 × 4 + (5 – 3)
(iii) 8 × 4 + 3
(iv) (9 × 3) + 2
Ans: Option (i) : 10 × 3 + (5 + 2)
Solution:
10 × 3 + (5 + 2)
= 30 + (7)
= 37
