Chapter 13 - Pythagoras' Theorem
Practice set 48
1. In the figures below, find the value of ‘x’.
(i)
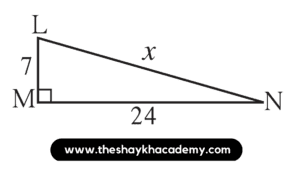
Given:
LM = 7 units
MN = 24 units
∠LMN = 90°
To find:
The value of x
Solution:
In ∆LMN, ∠LMN = 90°
∴ Side LN is the hypotenuse
According to Pythagoras’ theorem,
l(LN)² = l(LM)² + l(MN)²
∴ x² = 7² + 24²
∴ x² = 49 + 576
∴ x² = 625
∴ x² = 25²
∴ x = 25 units
Ans: The value of x is 25 units.
(ii)
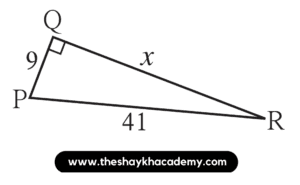
Given:
PQ = 9 units
PR = 41 units
∠PQR = 90°
To find:
The value of x
Solution:
In ∆PQR, ∠PQR = 90°
∴ Side PR is the hypotenuse
According to Pythagoras’ theorem,
l(PR)² = l(PQ)² + l(QR)²
∴ 41² = 9² + x²
∴ 1681 = 81 + x²
∴ 1681 – 81 = x²
∴ x² = 1600
∴ x² = 40²
∴ x = 40 units
Ans: The value of x is 40 units.
(iii)
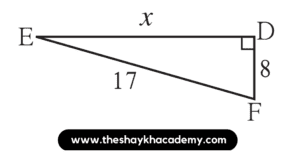
Given:
DF = 8 units
EF = 17 units
∠EDF = 90°
To find:
The value of x
Solution:
In ∆EDF, ∠EDF = 90°
∴ Side EF is the hypotenuse
According to Pythagoras’ theorem,
l(EF)² = l(ED)² + l(DF)²
∴ 17² = x² + 8²
∴ 289 = x² + 64
∴ 289 – 64 = x²
∴ x² = 225
∴ x² = 15²
∴ x = 15 units
Ans: The value of x is 15 units.
2. In the right-angled ∆PQR, ∠P = 90°. If l(PQ) = 24 cm and l(PR) = 10 cm, find the length of seg QR.
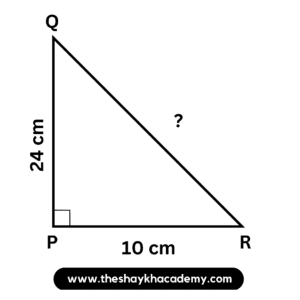
Given:
∠P = 90°
l(PQ) = 24 cm
l(PR) = 10 cm
To find:
l(QR)
Solution:
In ∆PQR, ∠P = 90°
∴ Side QR is the hypotenuse
According to Pythagoras’ theorem,
l(QR)² = l(PR)² + l(PQ)²
∴ l(QR)² = 10² + 24²
∴ l(QR)² = 100 + 576
∴ l(QR)² = 676
∴ l(QR)² = 26²
∴ l(QR) = 26 cm
Ans: The length of side QR is 26 cm.
3. In the right-angled ∆LMN, ∠M = 90°. If l(LM) = 12 cm and l(LN) = 20 cm, find the length of seg MN.
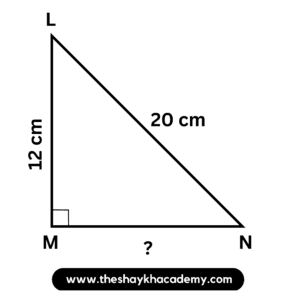
Given:
∠M = 90°
l(LM) = 12 cm
l(LN) = 20 cm
To find:
l(MN)
Solution:
In ∆LMN, ∠M = 90°
∴ Side LN is the hypotenuse
According to Pythagoras’ theorem,
l(LN)² = l(LM)² + l(MN)²
∴ 20² = 12² + l(MN)²
∴ l(MN)² = 20² – 12²
∴ l(MN)² = 400 – 144
∴ l(MN)² = 256
∴ l(MN)² = 16²
∴ l(MN)= 16 cm
Ans: The length of seg MN is 16 cm.
4. The top of a ladder of length 15 m reaches a window 9 m above the ground. What is the distance between the base of the wall and that of the ladder ?
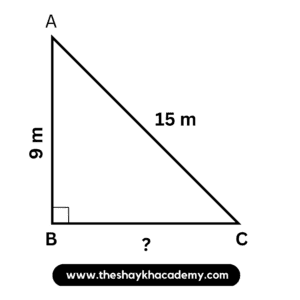
Given:
∠ABC = 90°
The top of the ladder i.e. l(AC) = 15 m
It reaches a window i.e. l(AB) = 9 m
To find:
The distance between the base of the wall and that of the ladder i.e. l(BC)
Solution:
The wall and the ground are perpendicular to each other and the ladder reaching the wall forms the hypotenuse to the right-angled triangle.
In ∆ABC, ∠ABC = 90°
∴ Side AC is the hypotenuse
According to Pythagoras’ theorem,
l(AC)² = l(AB)² + l(BC)²
∴ 15² = l(BC)² + 9²
∴ 225 = l(BC)² + 81
∴ 225 – 81 = l(BC)²
∴ l(BC)² = 144
∴ l(BC)² = 12²
∴ l(BC) = 12 m
Ans: The distance between the base of the wall and that of the ladder is 12 m.
Practice set 49
1. Find the Pythagorean triplets from among the following sets of numbers.
(i) 3, 4, 5
Given:
The numbers given are 3, 4, 5
To find:
Whether the numbers are a Pythagorean triplet
Solution:
The biggest of the three numbers is 5
Let 5 be the hypotenuse.
According to Pythagoras’ theorem,
5² = 3² + 4²
∴ 25 = 9 + 16
∴ 25 = 25 which is true
Ans: 3, 4, 5 is a Pythagorean triplet.
(ii) 2, 4, 5
Given:
The numbers given are 2, 4, 5
To find:
Whether the numbers is a Pythagorean triplet
Solution:
The biggest of the three numbers is 5
Let 5 be the hypotenuse.
According to Pythagoras’ theorem,
5² = 2² + 4²
∴ 25 = 4 + 16
∴ 25 ≠ 20
Ans: 2, 4, 5 is not a Pythagorean triplet.
(iii) 4, 5, 6
Given:
The numbers given are 4, 5, 6
To find:
Whether the numbers are a Pythagorean triplet
Solution:
The biggest of the three numbers is 6
Let 6 be the hypotenuse.
According to Pythagoras’ theorem,
6² = 4² + 5²
∴ 36 = 16 + 25
∴ 36 ≠ 41
Ans: 4, 5, 6 is not a Pythagorean triplet.
(iv) 2, 6, 7
Given:
The numbers given are 2, 6, 7
To find:
Whether the numbers are a Pythagorean triplet
Solution:
The biggest of the three numbers is 7
Let 7 be the hypotenuse.
According to Pythagoras’ theorem,
7² = 2² + 6²
∴ 49 = 4 + 36
∴ 49 ≠ 40
Ans: 2, 6, 7 is not a Pythagorean triplet.
(v) 9, 40, 41
Given:
The numbers given are 9, 40, 41
To find:
Whether the numbers are a Pythagorean triplet
Solution:
The biggest of the three numbers is 41
Let 41 be the hypotenuse.
According to Pythagoras’ theorem,
41² = 9² + 40²
∴ 1681 = 81 + 1600
∴ 1681 = 1681 which is true
Ans: 9, 40, 41 is a Pythagorean triplet.
(vi) 4, 7, 8
Given:
The numbers given are 4, 7, 8
To find:
Whether the numbers are a Pythagorean triplet
Solution:
The biggest of the three numbers is 8
Let 8 be the hypotenuse.
According to Pythagoras’ theorem,
8² = 4² + 7²
∴ 64 = 16 + 49
∴ 64 ≠ 65
Ans: 4, 7, 8 is not a Pythagorean triplet.
2. The sides of some triangles are given below. Find out which ones are right-angled triangles?
(i) 8, 15, 17
Given:
The sides of a triangle are 8, 15, 17
To find:
Whether the sides are of a right-angled triangle
Solution:
The biggest of the three numbers is 17
Let 17 be the hypotenuse.
According to Pythagoras’ theorem,
17² = 8² + 15²
∴ 289 = 64 + 225
∴ 289 = 289
Since the given numbers satisfies the pythagorean theorem
∴ The sides will form a right-angled triangle
Ans: The sides of lengths 8,15,17 will form a right-angled triangle.
(ii) 11, 12, 15
Given:
The sides of a triangle are 11, 12, 15
To find:
Whether the sides are of a right-angled triangle
Solution:
The biggest of the three numbers is 15
Let 15 be the hypotenuse.
According to Pythagoras’ theorem,
15² = 11² + 12²
∴ 225 = 121 + 144
∴ 225 ≠ 265
Since the given numbers does not satisfy the pythagorean theorem
∴ The sides will not form a right-angled triangle
Ans: The sides of lengths 11, 12, 15 will not form a right-angled triangle.
(iii) 11, 60, 61
Given:
The sides of a triangle are 11, 60, 61
To find:
Whether the sides are of a right-angled triangle
Solution:
The biggest of the three numbers is 61
Let 61 be the hypotenuse.
According to Pythagoras’ theorem,
61² = 11² + 60²
∴ 3721 = 121 + 3600
∴ 3721 = 3721
Since the given numbers satisfies the pythagorean theorem
∴ The sides will form a right-angled triangle
Ans: The sides of lengths 11, 60, 61 will form a right-angled triangle.
(iv) 1.5, 1.6, 1.7
Given:
The sides of a triangle are 1.5, 1.6, 1.7
To find:
Whether the sides are of a right-angled triangle
Solution:
The biggest of the three numbers is 1.7
Let 1.7 be the hypotenuse.
According to Pythagoras’ theorem,
1.7² = 1.5² + 1.6²
∴ 2.89 = 2.25 + 2.56
∴ 2.89 ≠ 4.81
Since the given numbers does not satisfy the pythagorean theorem
∴ The sides will not form a right-angled triangle
Ans: The sides of lengths 1.5, 1.6, 1.7 will not form a right-angled triangle.
(v) 40, 20, 30
Given:
The sides of a triangle are 40, 20, 30
To find:
Whether the sides are of a right-angled triangle
Solution:
The biggest of the three numbers is 40
Let 40 be the hypotenuse.
According to Pythagoras’ theorem,
40² = 20² + 30²
∴ 1600 = 400 + 900
∴ 1600 ≠ 1300
Since the given numbers does not satisfy the pythagorean theorem
∴ The sides will not form a right-angled triangle
Ans: The sides of lengths 40, 20, 30 will not form a right-angled triangle.
