Chapter 4 – Altitudes and Medians of a triangle
Practice set 4.1
1. In ∆ LMN, ___ is an altitude and ___ is a median. (write the names of appropriate segments.)
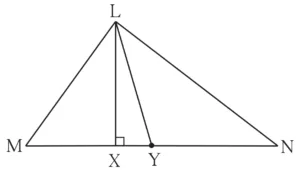
Ans: In ∆ LMN, ___ is an altitude and ___ is a median.
2. Draw an acute angled ∆ PQR. Draw all of its altitudes. Name the point of concurrence as ‘O’.
Solution:

3. Draw an obtuse angled ∆ STV. Draw its medians and show the centroid.
Solution:

4. Draw an obtuse angled ∆ LMN. Draw its altitudes and denote the orthocentre by ‘O’.
Solution:

5. Draw a right angled ∆ XYZ. Draw its medians and show their point of concurrence by G.
Solution:
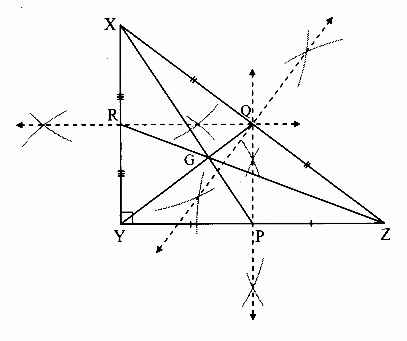
6. Draw an isosceles triangle. Draw all of its medians and altitudes. Write your observation about their points of concurrence.
Solution:
The point of concurrence of medians i.e. G and that of altitudes i.e. O lie on the same line PS which is the perpendicular bisector of seg QR.
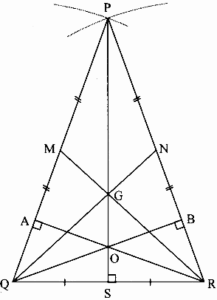
7. Fill in the blanks.
Point G is the centroid of ∆ ABC.

(1) If l(RG) = 2.5 then l(GC) = ___
Ans: The centroid of a triangle divides each median in the ratio 2:1.
Point G is the centroid and seg CR is the median.
∴ \(\large \frac {l(GC)}{l(RG)}\) = \(\large \frac {2}{1}\)
∴ \(\large \frac {l(GC)}{2.5}\) = \(\large \frac {2}{1}\)
∴ l(GC) × 1 = 2 × 2.5
∴ l(GC) = 5
(2) If l(BG) = 6 then l(BQ) = ___
Ans: The centroid of a triangle divides each median in the ratio 2:1.
Point G is the centroid and seg BQ is the median.
∴ \(\large \frac {l(BG)}{l(GQ)}\) = \(\large \frac {2}{1}\)
∴ \(\large \frac {6}{l(GQ)}\) = \(\large \frac {2}{1}\)
∴ 6 × 1 = 2 × l(GQ)
∴ \(\large \frac {6}{2}\) = l(GQ)
∴ l(GQ) = 3
Now, l (BQ) = l(BG) + l(GQ)
∴ l(BQ) = 6 + 3
∴ l(BQ) = 9
(3) If l(AP) = 6 then l(AG) = ___ and l(GP) = ___
Ans: The centroid of a triangle divides each median in the ratio 2:1.
Point G is the centroid and seg AP is the median.
∴ \(\large \frac {l(AG)}{l(GP)}\) = \(\large \frac {2}{1}\)
∴ l(AG) = 2 l(GP) …(i)
Now,
l(AP) = l(AG) + l(GP) …(ii)
∴ l(AP) = 2l(GP) + l(GP) … [From (i)]
∴ l(AP) = 3l(GP)
∴ 6 = 3l(GP) ..[∵ l(AP) = 6]
∴ \(\large \frac {6}{3}\) = l(GP)
∴ l(GP) = 2
And,
l(AP) = l(AG) + l(GP) …[from (ii)]
∴ 6 = l(AG) + 2
∴ l(AG) = 6 – 2
∴ l(AG) = 4
