Chapter 5 – Co-ordinate Geometry
Practice set 5.1
1. Find the distance between each of the following pairs of points.
(1) A(2, 3), B(4, 1)
Solution:
A(2, 3) = (x₁, y₁)
B(4, 1) = (x₂, y₂)
By distance formula,
d(A, B) = \(\sqrt{(x₂\,–\,x₁)^2\,+\,(y₂\,–\,y₁)^2}\)
∴ d(A, B) = \(\sqrt{(4\,–\,2)^2\,+\,(1\,–\,3)^2}\)
∴ d(A, B) = \(\sqrt{(2)^2\,+\,(–\,2)^2}\)
∴ d(A, B) = \(\sqrt{4\,+\,4}\)
∴ d(A, B) = \(\sqrt{2(4)}\)
∴ d(A, B) = 2\(\sqrt{2}\) units
Ans: d(A, B) = 2\(\sqrt{2}\) units
(2) P(– 5, 7), Q(– 1, 3)
Solution:
P(–5, 7) = (x₁, y₁)
Q(–1, 3) = (x₂, y₂)
By distance formula,
d(P, Q) = \(\sqrt{(x₂\,–\,x₁)^2\,+\,(y₂\,–\,y₁)^2}\)
∴ d(P, Q) = \(\sqrt{[–\,1\,–\,(–\,5)]^2\,+\,(3\,–\,7)^2}\)
∴ d(P, Q) = \(\sqrt{(–\,1\,+\,5)^2\,+\,(–\,4)^2}\)
∴ d(P, Q) = \(\sqrt{(4)^2\,+\,16}\)
∴ d(P, Q) = \(\sqrt{16\,+\,16}\)
∴ d(P, Q) = \(\sqrt{2(16)}\)
∴ d(P, Q) = 4\(\sqrt{2}\) units
Ans: d(P, Q) = 4\(\sqrt{2}\) units
(3) R(0, – 3), S\(\large(\)0, \(\large \frac {5}{2})\)
Solution:
R(0, –3) = (x₁, y₁)
S\(\large(\)0, \(\large \frac {5}{2})\) = (x₂, y₂)
By distance formula,
d(R, S) = \(\sqrt{(x₂\,–\,x₁)^2\,+\,(y₂\,–\,y₁)^2}\)
∴ d(R, S) = \(\sqrt{(0\,–\,0)^2\,+\,\large (\frac {5}{2}\,–\,\small(–\,3))^{2}}\)
∴ d(R, S) = \(\sqrt{(0)^2\,+\,\large (\frac {5}{2}\,+\small\,3)^{2}}\)
∴ d(R, S) = \(\sqrt{0\,+\,\large (\frac {11}{2})^{2}}\)
∴ d(R, S) = \(\sqrt{\large (\frac {11}{2})^{2}}\)
∴ d(R, S) = \(\large \frac {5}{2}\)
Ans: d(R, S) = \(\large \frac {5}{2}\) units.
(4) L(5, – 8), M(– 7, – 3)
Solution:
L(5, – 8) = (x₁, y₁)
M(– 7, – 3) = (x₂, y₂)
By distance formula,
d(L, M) = \(\sqrt{(x₂\,–\,x₁)^2\,+\,(y₂\,–\,y₁)^2}\)
∴ d(L, M) = \(\sqrt{(4\,–\,2)^2\,+\,(1\,–\,3)^2}\)
∴ d(L, M) = \(\sqrt{(2)^2\,+\,(–\,2)^2}\)
∴ d(L, M) = \(\sqrt{4\,+\,4}\)
∴ d(L, M) = \(\sqrt{2(4)}\)
∴ d(L, M) = 2\(\sqrt{2}\) units
Ans: d(L, M) = 2\(\sqrt{2}\) units
(5) T(– 3, 6), R(9, – 10)
Solution:
T(– 3, 6) = (x₁, y₁)
R(9, – 10) = (x₂, y₂)
By distance formula,
d(T, R) = \(\sqrt{(x₂\,–\,x₁)^2\,+\,(y₂\,–\,y₁)^2}\)
∴ d(T, R) = \(\sqrt{(9\,–\,(–\,3))^2\,+\,((–\,10)\,–\,6)^2}\)
∴ d(T, R) = \(\sqrt{(9\,+\,3)^2\,+\,(–\,10\,–\,6)^2}\)
∴ d(T, R) = \(\sqrt{(12)^2\,+\,(–\,16)^2}\)
∴ d(T, R) = \(\sqrt{144\,+\,256}\)
∴ d(T, R) = \(\sqrt{400}\)
∴ d(T, R) = 20 units
Ans: d(T, R) = 20 units
(6) W\(\large (\frac {–\,7}{2}\) , 4), X(11, 4)
Solution:
W\(\large (\frac {–\,7}{2}\) , 4) = (x₁, y₁)
X(11, 4) = (x₂, y₂)
By distance formula,
d(W, X) = \(\sqrt{(x₂\,–\,x₁)^2\,+\,(y₂\,–\,y₁)^2}\)
∴ d(W, X) = \(\sqrt{(11\,–\,(\large \frac {–\,7}{2}))^2\,+\,\small (4\,–\,4)^2}\)
∴ d(W, X) = \(\sqrt{(11\,+\,\large \frac {7}{2})^2+\,\small (0)^2}\)
∴ d(W, X) = \(\sqrt{\large (\frac {11\,×\,2\,+\,7}{2})^2}\)
∴ d(W, X) = \(\sqrt{\large (\frac {22\,+\,7}{2})^2}\)
∴ d(W, X) = \(\sqrt{\large (\frac {29}{2})^2}\)
∴ d(W, X) = \(\large \frac {29}{2}\) units
Ans: d(W, X) = \(\large \frac {29}{2}\) units
2. Determine whether the points are collinear.
(1) A(1, – 3), B(2, – 5), C(– 4, 7)
Solution:
A(1, – 3) = (x₁, y₁)
B(2, – 5) = (x₂, y₂)
C(– 4, 7) = (x₃, y₃)
Slope of line AB
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {–\,5\,–\,(–\,3)}{2\,–\,1}\)
= \(\large \frac {–\,5\,+\,3}{1}\)
= – 2 …(i)
Slope of line BC
= \(\large \frac {y₃\,–\,y₂}{x₃\,–\,x₂}\)
= \(\large \frac {7\,–\,(–\,5)}{–\,4\,–\,2}\)
= \(\large \frac {7\,+\,5}{–\,6}\)
= \(\large \frac {12}{–\,6}\)
= – 2 …(i)
∴ Slope of line AB = Slope of line BC …[From (i) and (ii)]
Line AB and line BC have equal slopes and have a common point B.
∴ Points A, B and C are collinear.
(2) L(– 2, 3), M(1, – 3), N(5, 4)
Solution:
L(– 2, 3) = (x₁, y₁)
M(1, – 3) = (x₂, y₂)
N(5, 4) = (x₃, y₃)
Slope of line LM
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {–\,3\,–\,3}{1\,–\,(–\,2)}\)
= \(\large \frac {–\,6}{1\,+\,2}\)
= \(\large \frac {–\,6}{3}\)
= – 2 …(i)
Slope of line MN
= \(\large \frac {y₃\,–\,y₂}{x₃\,–\,x₂}\)
= \(\large \frac {4\,–\,(–\,3)}{5\,–\,1}\)
= \(\large \frac {4\,+\,3}{4}\)
= \(\large \frac {7}{4}\) …(ii)
∴ Slope of line LM ≠ Slope of line MN …[From (i) and (ii)]
Line LM and line MN have equal slopes and have a common point M.
∴ Points L, M and N are collinear.
(3) R(0, 3), D(2, 1), S(3, – 1)
Solution:
R(0, 3) = (x₁, y₁)
D(2, 1) = (x₂, y₂)
S(3, – 1) = (x₃, y₃)
Slope of line RD
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {1\,–\,3}{2\,–\,0}\)
= \(\large \frac {–\,2}{2}\)
= – 1 …(i)
Slope of line DS
= \(\large \frac {y₃\,–\,y₂}{x₃\,–\,x₂}\)
= \(\large \frac {–\,1\,–\,1}{3\,–\,2}\)
= \(\large \frac {–\,2}{1}\)
= – 2 …(i)
∴ Slope of line RD = Slope of line DS …[From (i) and (ii)]
Line RD and line DS have equal slopes and have a common point D.
∴ Points R, D and S are collinear.
(4) P(– 2, 3), Q(1, 2), R(4, 1)
Solution:
P(– 2, 3) = (x₁, y₁)
Q(1, 2) = (x₂, y₂)
R(4, 1) = (x₃, y₃)
Slope of line PQ
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {2\,–\,3}{1\,–\,(–\,2)}\)
= \(\large \frac {–\,1}{1\,+\,2}\)
= \(\large \frac {–\,1}{3}\) …(i)
Slope of line QR
= \(\large \frac {y₃\,–\,y₂}{x₃\,–\,x₂}\)
= \(\large \frac {1\,–\,2}{4\,–\,1}\)
= \(\large \frac {–\,1}{–\,3}\) …(ii)
∴ Slope of line PQ = Slope of line QR …[From (i) and (ii)]
Line PQ and line QR have equal slopes and have a common point Q.
∴ Points P, Q and R are collinear.
3. Find the point on the X – axis which is equidistant from A(– 3, 4) and B(1, – 4).
Solution:
Let P(x, 0) be a point on the X axis which is equidistant from A(– 3, 4) and B(1, – 4).
d(P, A) = d(P, B)
By distance formula,
\(\sqrt{[x\,–\,(–\,3)]^2\,+\,(0\,–\,4)^2}\) = \(\sqrt{(x\,–\,1)^2\,+\,[0\,–\,(–\,4)]^2}\)
∴ \(\sqrt{(x\,+\,3)^2\,+\,(–\,4)^2}\) = \(\sqrt{(x\,–\,1)^2\,+\,(0\,+\,4)^2}\)
∴ \(\sqrt{(x\,+\,3)^2\,+\,(–\,4)^2}\) = \(\sqrt{(x\,–\,1)^2\,+\,(4)^2}\)
Squaring both the sides we get,
(x + 3)² + 16 = (x – 1)² + 16
∴ x² + 6x + 9 = x² – 2x + 1
∴ x² + 6x – x² + 2x = 1 – 9
∴ 8x = – 8
∴ x = – 1
Ans: P(– 1, 0) is the required point.
4. Verify that points P(– 2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle.
Solution:
P(–2, 2), Q(2, 2) and R(2, 7) be the vertices of a triangle
Using distance formula,
d(P, Q) = \(\sqrt{(–\,2\,–\,2)^2\,+\,(2\,–\,2)^2}\)
∴ d(P, Q) = \(\sqrt{(–\,4)^2\,+\,(0)^2}\)
∴ d(P, Q) = \(\sqrt{16}\)
∴ d(P, Q) = 4 units
d(Q, R) = \(\sqrt{(2\,–\,2)^2\,+\,(2\,–\,7)^2}\)
∴ d(Q, R) = \(\sqrt{(0)^2\,+\,(–\,5)^2}\)
∴ d(Q, R) = \(\sqrt{5^2}\)
∴ d(Q, R) = 5 units
∴ d(P, R) = \(\sqrt{(–\,2\,–\,2)^2\,+\,(2\,–\,7)^2}\)
∴ d(P, R) = \(\sqrt{(–\,4)^2\,+\,(–\,5)^2}\)
∴ d(P, R) = \(\sqrt{16\,+\,25}\)
∴ d(P, R) = \(\sqrt{41}\) units
∴ PR² = 41 …(i)
PQ² + QR² = 4² + 5²
∴ PQ² + QR² = 16 + 25
∴ PQ² + QR² = 41 …(ii)
∴ PR² = PQ² + QR² …[From (i) and (ii)]
∴ ∆PQR is a right angled triangle …[Converse of Pythagoras theorem]
Hence proved.
5. Show that points P(2, – 2), Q(7, 3), R(11, – 1) and S (6, – 6) are vertices of a parallelogram.
Solution:
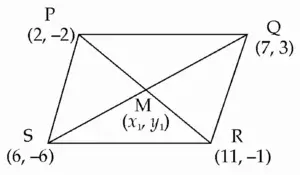
Let M (x₁, y₁) be the midpoint of diagonal PR.
By midpoint formula,
x₁ = \(\large \frac {2\,+\,11}{2}\)
x₁ = \(\large \frac {13}{2}\)
y₁ = \(\large \frac {–\,2\,–\,1}{2}\)
y₁ = \(\large \frac {–\,3}{2}\)
M \(\large (\frac {13}{2}\) , \(\large \frac {–\,3}{2})\) is the midpoint of diagonal PR …(i)
Let N(x₂, y₂) be the midpoint of diagonal QS.
By midpoint formula,
x₂ = \(\large \frac {7\,+\,6}{2}\)
x₂ = \(\large \frac {13}{2}\)
y₂ = \(\large \frac {3\,+\,(–\,6)}{2}\)
y₂ = \(\large \frac {–\,3}{2}\)
N \(\large (\frac {13}{2}\) , \(\large \frac {–\,3}{2})\) is the midpoint of diagonal QS …(ii)
Midpoint of diagonal PR and diagonal QS is the same i.e. Diagonals PR and QS bisect each other.
∴ PQRS is a parallelogram …[A quadrilateral is a parallelogram if its diagonals bisect each other]
Hence proved.
6. Show that points A(– 4, – 7), B(– 1, 2), C(8, 5) and D(5, – 4) are vertices of a rhombus ABCD.
Solution:
A(– 4, – 7), B(– 1, 2), C(8, 5) and D(5, – 4) are the vertical it a quadrilateral
By distance formula,
d(A, B) = \(\sqrt{[–\,4\,–\,(–\,1)]^2\,+\,(7\,–\,2)^2}\)
∴ d(A, B) = \(\sqrt{(–\,3)^2\,+\,(–\,9)^2}\)
∴ d(A, B) = \(\sqrt{9\,+\,81}\)
∴ d(A, B) = \(\sqrt{90}\) units …(i)
d(B, C) = \(\sqrt{(–\,1\,–\,8)^2\,+\,(2\,–\,5)^2}\)
∴ d(B, C) = \(\sqrt{(–\,9)^2\,+\,(–\,3)^2}\)
∴ d(B, C) = \(\sqrt{81\,+\,9}\)
∴ d(B, C) = \(\sqrt{90}\) units …(ii)
d(C, D) = \(\sqrt{(8\,–\,5)^2\,+\,[5\,–\,(–\,4)]^2}\)
∴ d(C, D) = \(\sqrt{(–\,3)^2\,+\,(5\,+\,4)^2}\)
∴ d(C, D) = \(\sqrt{9\,+\,9^2}\)
∴ d(C, D) = \(\sqrt{9\,+\,81}\)
∴ d(C, D) = \(\sqrt{90}\) units …(iii)
d(A, D) = \(\sqrt{(–\,4\,–\,5)^2\,+\,[–\,7\,–\,(–\,4)]^2}\)
∴ d(A, D) = \(\sqrt{(–\,9)^2\,+\,(–\,3)^2}\)
∴ d(A, D) = \(\sqrt{81\,+\,9}\)
∴ d(A, D) = \(\sqrt{90}\) units …(iv)
∴ AB = BC = CD = AD …[From (i), (ii), (iii) and (iv)]
∴ ABCD is a rhombus. …[By Definition]
Hence proved.
7. Find x if the distance between points L(x, 7) and M(1, 15) is 10.
Solution:
L(x, 7) and M(1, 15)
By distance formula,
d(L, M) = \(\sqrt{[(x\,–\,1)^2\,+\,(7\,–\,15)]^2}\)
∴ 10 = \(\sqrt{[(x\,–\,1)^2\,+\,(–\,8)]^2}\)
Squaring both the sides we get,
100 = (x – 1)² + 64
∴ 100 – 64 = (x – 1)²
∴ (x – 1)² = 36
∴ x – 1 = ± 6 …[Taking square roots]
∴ x – 1 = 6 or x – 1 = – 6
∴ x = 6 + 1 or x = – 6 + 1
∴ x = 7 or x = – 5
Ans: x = 7 or x = – 5
8. Show that the points A(1, 2), B(1, 6), C(1 + 2\(\sqrt{3}\), 4) are vertices of an equilateral triangle.
Solution:
A(1, 2), B(1, 6) and C(1 + 2\(\sqrt{3}\) be the vertices of triangle
Using distance formula,
d(A, B) = \(\sqrt{(1\,–\,1)^2\,+\,(2\,–\,6)^2}\)
∴ d(A, B) = \(\sqrt{(0)^2\,+\,(–\,4)^2}\)
∴ d(A, B) = \(\sqrt{0\,+\,16}\)
∴ d(A, B) = \(\sqrt{16}\)
∴ d(A, B) = 4 units …(i)
d(B, C) = \(\sqrt{(1\,+\,2\sqrt{3}\,–\,1)^2\,+\,(4\,–\,6)^2}\)
∴ d(B, C) = \(\sqrt{(2\sqrt{3})^2\,+\,(–\,2)^2}\)
∴ d(B, C) = \(\sqrt{12\,+\,4}\)
∴ d(B, C) = \(\sqrt{16}\)
∴ d(B, C) = 4 units …(ii)
d(A, C) = \(\sqrt{(1\,+\,2\sqrt{3}\,–\,1)^2\,+\,(4\,–\,2)^2}\)
∴ d(A, C) = \(\sqrt{(2\sqrt{3})^2\,+\,(2)^2}\)
∴ d(A, C) = \(\sqrt{12\,+\,4}\)
∴ d(A, C) = \(\sqrt{16}\)
∴ d(A, C) = 4 units …(iii)
∴ d(A, C) = 4 units …(iii)
∴ AB = BC = AC …[From (i), (ii) and (iii)]
∴ ∆ABC is an equilateral triangle …[By Definition]
Hence proved.
Practice set 5.2
1. Find the coordinates of point P if P divides the line segment joining the points A(– 1, 7) and B(4, – 3) in the ratio 2 : 3.
Solution:
P(x, y) divides seg AB in the ratio 2 : 3.
A(– 1, 7) = (x₁, y₁)
B(4, – 3) = (x₂, y₂)
m : n = 2 : 3
By Section formula,
x = \(\large \frac {mx₂\,+\,nx₁}{m\,+\,n}\)
∴ x = \(\large \frac {2(4)\,+\,3(–\,1)}{2\,+\,3}\)
∴ x = \(\large \frac {8\,–\,3}{5}\)
∴ x = \(\large \frac {5}{5}\)
∴ x = 1
y = \(\large \frac {my₂\,+\,ny₁}{m\,+\,n}\)
∴ y = \(\large \frac {2(–\,3)\,+\,3(7)}{2\,+\,3}\)
∴ y = \(\large \frac {–\,6\,+\,21}{5}\)
∴ y = \(\large \frac {15}{5}\)
∴ y = 3
Ans: The coordinates of point P are (1, 3).
2. In each of the following examples find the co – ordinates of point A which divides segment PQ in the ratio a : b.
(1) P(– 3, 7), Q(1, – 4), a : b = 2 : 1
Solution:
A(x, y) divides seg PQ in the ratio 2 : 1.
P(– 3, 7) = (x₁, y₁)
Q(1, – 4) = (x₂, y₂)
a : b = 2 : 1 = m : n
By Section formula,
x = \(\large \frac {mx₂\,+\,nx₁}{m\,+\,n}\)
∴ x = \(\large \frac {2(1)\,+\,1(–\,3)}{2\,+\,1}\)
∴ x = \(\large \frac {2\,–\,3}{3}\)
∴ x = \(\large \frac {–\,1}{3}\)
y = \(\large \frac {my₂\,+\,ny₁}{m\,+\,n}\)
∴ y = \(\large \frac {2(–\,4)\,+\,1(7)}{2\,+\,1}\)
∴ y = \(\large \frac {–\,8\,+\,7}{3}\)
∴ y = \(\large \frac {–\,1}{3}\)
Ans: The coordinates of point A are \(\large (\frac {–\,1}{3}\), \(\large \frac {–\,1}{3})\).
(2) P(– 2, – 5), Q(4, 3), a : b = 3 : 4
Solution:
A(x, y) divides seg PQ in the ratio 3 : 4.
P(– 2, – 5) = (x₁, y₁)
Q(4, 3) = (x₂, y₂)
a : b = 3 : 4 = m : n
By Section formula,
x = \(\large \frac {mx₂\,+\,nx₁}{m\,+\,n}\)
∴ x = \(\large \frac {3(4)\,+\,4(–\,2)}{3\,+\,4}\)
∴ x = \(\large \frac {12\,–\,8}{7}\)
∴ x = \(\large \frac {4}{7}\)
y = \(\large \frac {my₂\,+\,ny₁}{m\,+\,n}\)
∴ y = \(\large \frac {3(3)\,+\,4(–\,5)}{3\,+\,4}\)
∴ y = \(\large \frac {9\,–\,20}{7}\)
∴ y = \(\large \frac {–\,11}{7}\)
Ans: The coordinates of point A are \(\large (\frac {4}{7}\), \(\large \frac {–\,11}{7})\).
(3) P(2, 6), Q(– 4, 1), a : b = 1 : 2
Solution:
A(x, y) divides seg PQ in the ratio 1 : 2.
P(2, 6) = (x₁, y₁)
Q(– 4, 1) = (x₂, y₂)
a : b = 1 : 2 = m : n
By Section formula,
x = \(\large \frac {mx₂\,+\,nx₁}{m\,+\,n}\)
∴ x = \(\large \frac {1(–\,4)\,+\,2(2)}{1\,+\,2}\)
∴ x = \(\large \frac {–\,4\,+\,4}{3}\)
∴ x = \(\large \frac {0}{3}\)
∴ x = 0
y = \(\large \frac {my₂\,+\,ny₁}{m\,+\,n}\)
∴ y = \(\large \frac {1(1)\,+\,2(6)}{1\,+\,2}\)
∴ y = \(\large \frac {1\,+\,12}{3}\)
∴ y = \(\large \frac {13}{3}\)
Ans: The coordinates of point A are \(\large (\)0, \(\large \frac {13}{3})\).
3. Find the ratio in which point T(– 1, 6) divides the line segment joining the points P(– 3, 10) and Q(6, – 8).
Solution:
Let point T divides seg PQ in the ratio m : n.
T(– 1, 6) = (x, y)
P(– 3, 10) = (x₁, y₁)
Q(6, – 8) = (x₂, y₂)
By Section formula,
x = \(\large \frac {mx₂\,+\,nx₁}{m\,+\,n}\)
∴ – 1 = \(\large \frac {m(6)\,+\,n(–\,3)}{m\,+\,n}\)
∴ – 1(m + n) = 6m – 3n
∴ – m – n = 6m – 3n
∴ – m – 6m = n – 3n
∴ – 7m = – 2n
∴ 7m = 2n
∴ \(\large \frac {m}{n}\) = \(\large \frac {2}{7}\)
∴ m : n = 2 : 7
Ans: Point T divides seg PQ in the ratio 2 : 7.
4. Point P is the centre of the circle and AB is a diameter. Find the coordinates of point B if coordinates of point A and P are (2, – 3) and (– 2, 0) respectively.
Solution:
P(– 2, 0) = (x, y)
A(2, – 3) = (x₁, y₁)
B(x₂, y₂) = ?
P is the centre of the circle …[Given]
Point P is the midpoint of diameter AB.
By midpoint formula,
x = \(\large \frac {x₁\,+\,x₂}{2}\)
∴ – 2 = \(\large \frac {2\,+\,x₂}{2}\)
∴ – 2 × 2 = 2 + x₂
∴ – 4 – 2 = x₂
∴ x₂ = – 6
y = \(\large \frac {y₁\,+\,y₂}{2}\)
∴ 0 = \(\large \frac {–\,3\,+\,y₂}{2}\)
∴ 0 × 2 = – 3 + y₂
∴ 0 + 3 = y₂
∴ y₂ = 3
∴ B(x₂, y₂) = (– 6, 3)
Ans: B(x₂, y₂) = (– 6, 3)
5. Find the ratio in which point P(k, 7) divides the segment joining A(8, 9) and B(1, 2). Also find k.
Solution:
A(8, 9) = (x1, y1)
B(1, 2) = (x2, y2)
P(k, 7) = (x, y)
Let point P divide seg AB in the ratio m : n.
By Section formula,
y = \(\large \frac {my₂\,+\,ny₁}{m\,+\,n}\)
∴ 7 = \(\large \frac {m(2)\,+\,n(9)}{m\,+\,n}\)
∴ 7 (m + n) = 2m + 9n
∴ 7m + 7n = 2m + 9n
∴ 7m – 2m = 9n – 7n
∴ 5m = 2n
∴ \(\large \frac {m}{n}\) = \(\large \frac {2}{5}\)
∴ m : n = 2 : 5
x = \(\large \frac {mx₂\,+\,nx₁}{m\,+\,n}\)
∴ k = \(\large \frac {2(1)\,+\,5(8)}{2\,+\,5}\)
∴ k = \(\large \frac {2\,+\,40}{7}\)
∴ k = \(\large \frac {42}{7}\)
∴ k = 6
Ans: The ratio is 2:5 and the value of k is 6.
6. Find the coordinates of the midpoint of the segment joining the points (22, 20) and (0, 16).
Solution:
Let A(22, 20) = (x₁, y₁) and B (0, 16) = (x₂, y₂)
Let M (x, y) be the midpoint of seg AB.
By midpoint formula,
x = \(\large \frac {x₁\,+\,x₂}{2}\)
∴ x = \(\large \frac {22\,+\,0}{2}\)
∴ x = \(\large \frac {22}{2}\)
∴ x = 11
y = \(\large \frac {y₁\,+\,y₂}{2}\)
∴ y = \(\large \frac {20\,+\,16}{2}\)
∴ y = \(\large \frac {36}{2}\)
∴ y = 18
∴ M(x, y) = (11, 18)
Ans: M(x, y) = (11, 18)
7. Find the centroids of the triangles whose vertices are given below.
(1) (– 7, 6), (2, – 2), (8, 5)
Solution:
Let A(–7, 6) = (x₁, y₁)
B(2, –2) = (x₂, y₂)
C(8, 5) = (x₃, y₃) be the vertices of ABC
Let G(x, y) be the centroid of ∆ABC.
By centroid formula,
x = \(\large \frac {x₁\,+\,x₂\,+\,x₃}{3}\)
∴ x = \(\large \frac {–\,7\,+\,2\,+\,8}{3}\)
∴ x = \(\large \frac {3}{3}\)
∴ x = 1
y = \(\large \frac {y₁\,+\,y₂\,+\,y₃}{3}\)
∴ y = \(\large \frac {6\,+\,–\,2\,+\,5}{3}\)
∴ y = \(\large \frac {9}{3}\)
∴ y = 3
∴ G = (1, 3)
Ans: The centroid is G (1, 3).
(2) (3, – 5), (4, 3), (11, – 4)
Solution:
Let A(3, – 5) = (x₁, y₁)
B(4, 3) = (x₂, y₂)
C(11, – 4) = (x₃, y₃) be the vertices of ABC
Let G(x, y) be the centroid of ∆ABC .
By centroid formula,
x = \(\large \frac {x₁\,+\,x₂\,+\,x₃}{3}\)
∴ x = \(\large \frac {3\,+\,4\,+\,11}{3}\)
∴ x = \(\large \frac {18}{3}\)
∴ x = 6
y = \(\large \frac {y₁\,+\,y₂\,+\,y₃}{3}\)
∴ y = \(\large \frac {–\,5\,+\,3\,+\,–\,4}{3}\)
∴ y = \(\large \frac {–\,6}{3}\)
∴ y = – 2
∴ G = (6, – 2)
Ans: The centroid is G (6, – 2).
(3) (4, 7), (8, 4), (7, 11)
Solution:
Let A(4, 7) = (x₁, y₁)
B(8, 4) = (x₂, y₂)
C(7, 11) = (x₃, y₃) be the vertices of ABC
Let G(x, y) be the centroid of ∆ABC .
By centroid formula,
x = \(\large \frac {x₁\,+\,x₂\,+\,x₃}{3}\)
∴ x = \(\large \frac {4\,+\,8\,+\,7}{3}\)
∴ x = \(\large \frac {19}{3}\)
y = \(\large \frac {y₁\,+\,y₂\,+\,y₃}{3}\)
∴ y = \(\large \frac {7\,+\,4\,+\,11}{3}\)
∴ y = \(\large \frac {22}{3}\)
∴ G = \(\large (\frac {19}{3}\) , \(\large \frac {22}{3})\)
Ans: The centroid is G \(\large (\frac {19}{3}\) , \(\large \frac {22}{3})\)
8. In ∆ABC, G(– 4, – 7) is the centroid. If A(– 14, – 19) and B(3, 5) then find the co– ordinates of C.
Solution:
A(– 14, – 19) = (x₁, y₁)
B(3, 5) = (x₂, y₂)
Let C (x₃, y₃)
G(– 4, – 7) = (x, y)
Point G is the centroid of ∆ABC.
By centroid formula,
x = \(\large \frac {x₁\,+\,x₂\,+\,x₃}{3}\)
∴ – 4 = \(\large \frac {–\,14\,+\,3\,+\,x₃}{3}\)
∴ – 4 × 3 = – 11 + x₃
∴ – 12 = – 11 + x₃
∴ – 12 + 11 = x₃
∴ x₃ = – 1
y = \(\large \frac {y₁\,+\,y₂\,+\,y₃}{3}\)
∴ – 7 = \(\large \frac {–\,19\,+\,5\,+\,y₃}{3}\)
∴ – 7 × 3 = – 14 + y₃
∴ – 21 = – 14 + y₃
∴ y₃ = – 21 + 14
∴ y₃ = – 7
∴ C(x₃, y₃) = (– 1, – 7)
Ans: The value of C is (– 1, – 7).
9. A(h, – 6), B(2, 3) and C(– 6, k) are the coordinates of vertices of a triangle whose centroid is G(1, 5). Find h and k.
Solution:
Let A(h, – 6) = (x₁, y₁)
B(2, 3) = (x₂, y₂)
and C(– 6, k) = (x₃, y₃)
G(1, 5) = (x, y)
Point G is the centroid of ∆ABC .
By centroid formula,
x = \(\large \frac {x₁\,+\,x₂\,+\,x₃}{3}\)
∴ 1 = \(\large \frac {h\,+\,2\,+\,–\,6}{3}\)
∴ 1 × 3 = h – 4
∴ 3 + 4 = h
∴ h = 7
y = \(\large \frac {y₁\,+\,y₂\,+\,y₃}{3}\)
∴ 5 = \(\large \frac {–\,6\,+\,3\,+\,k}{3}\)
∴ 5 × 3 = – 3 + k
∴ 15 = – 3 + k
∴ k = 15 + 3
∴ k = 18
Ans: The value of h is 7 and k is 18.
10. Find the co– ordinates of the points of trisection of the line segment AB with A(2, 7) and B(– 4, – 8).
Solution:

Let point P and Q be two points which divide seg AB in three equal parts.
Point P divides seg AB in the ratio 1 : 2
By Section formula,
P \(\large (\frac {mx₂\,+\,nx₁}{m\,+\,n}\) , \(\large \frac {my₂\,+\,ny₁}{m\,+\,n})\)
∴ P \(\large (\frac {1(–\,4)\,+\,2(2)}{1\,+\,2}\) , \(\large \frac {1(–\,8)\,+\,2(7)}{1\,+\,2})\)
∴ P \(\large (\frac {–\,4\,+\,4}{3}\) , \(\large \frac {–\,8\,+\,14}{3})\)
∴ P \(\large (\frac {0}{3}\) , \(\large \frac {6}{3})\)
∴ P (0, 2)
Also, PQ = QB
∴ Point Q is midpoint of seg PB.
By midpoint formula,
Q \(\large (\frac {0\,+\,(–\,4)}{2}\) , \(\large \frac {2\,+\,(–\,8)}{2})\)
∴ Q \(\large (\frac {–\,4}{2}\) , \(\large \frac {–\,6}{2})\)
∴ Q (– 2, – 3)
Ans: P(0, 2) and Q(– 2, – 3) are points which trisects seg AB.
11. If A (– 14, – 10), B(6, – 2) is given, find the coordinates of the points which divide segment AB into four equal parts.
Solution:
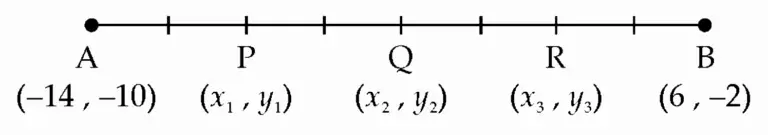
Let point P(x₁, y₁), Q (x₂, y₂) and R(x₃, y₃) be the three points which divide seg AB in four equal parts.
Point Q is the midpoint of seg AB.
By midpoint formula,
x₂ = \(\large (\frac {–\,14\,+\,6}{2}\)
∴ x₂ = \(\large (\frac {–\,8}{2}\)
∴ x₂ = – 4
y₂ = \(\large (\frac {–\,10\,+\,(–\,2)}{2}\)
∴ y₂ = \(\large (\frac {–\,12}{2}\)
∴ y₂ = – 6
∴ Q (– 4, – 6)
AP = PQ …[From (i)]
∴ P is the midpoint of seg AQ.
By midpoint formula,
x₁ = \(\large (\frac {–\,14\,+\,(–\,4)}{2}\)
∴ x₁ = \(\large (\frac {–\,14\,–\,4}{2}\)
∴ x₁ = \(\large (\frac {–\,18}{2}\)
∴ x₁ = – 9
y₁ = \(\large (\frac {–\,10\,+\,(–\,6)}{2}\)
∴ y₁ = \(\large (\frac {–\,10\,–\,6}{2}\)
∴ y₁ = \(\large (\frac {–\,16}{2}\)
∴ y₁ = – 8
∴ P (– 9, – 8)
∴ QR = BR …[From (i)]
R is the midpoint of seg BQ.
By midpoint formula,
x₃ = \(\large (\frac {–\,4\,+\,6}{2}\)
∴ x₃ = \(\large (\frac {2}{2}\)
∴ x₃ = 1
y₃ = \(\large (\frac {–\,6\,+\,(–\,2)}{2}\)
∴ y₃ = \(\large (\frac {–\,6\,–\,2}{2}\)
∴ y₃ = \(\large (\frac {–\,8}{2}\)
∴ y₃ = – 4
∴ R (1, – 4)
Ans: P(– 9, – 8), Q(– 4, – 6) and R(1, – 4) divides seg AB in four equal parts.
12. If A (20, 10), B(0, 20) are given, find the coordinates of the points which divide segment AB into five congruent parts.
Solution:
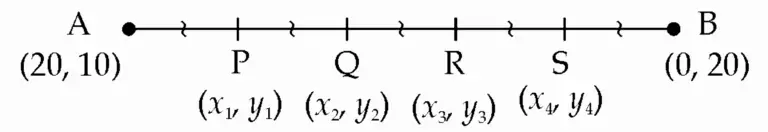
Let point P(x₁, y₁), Q (x₂, y₂), R(x₃, y₃) and S(x₄, y₄) be four points which divide seg AB into five congruent parts.
Point P divides seg AB in the ratio 1 : 4.
By section formula,
x₁ = \(\large \frac {1(0)\,+\,4(20)}{1\,+\,4}\)
∴ x₁ = \(\large \frac {0\,+\,80}{5}\)
∴ x₁ = \(\large \frac {80}{5}\)
∴ x₁ = 16
y₁ = \(\large \frac {1(20)\,+\,4(10)}{1\,+\,4}\)
∴ y₁ = \(\large \frac {20\,+\,40}{5\)
∴ y₁ = \(\large \frac {60}{5}\)
∴ y₁ = 12
∴ x₁ = 16 and y₁ = 12
∴ P(16, 12)
AP = PQ …[From (i)]
∴ P is the midpoint of seg AQ.
By midpoint formula,
16 = \(\large \frac {20\,+\,x₂}{2}\)
∴ 16 × 2 = 20 + x₂
∴ 32 = 20 + x₂
∴ 32 – 20 = x₂
∴ x₂ = 12
12 = \(\large \frac {10\,+\,y₂}{2}\)
∴ 12 × 2 = 10 + y₂
∴ 24 = 10 + y₂
∴ 24 – 10 = y₂
∴ y₂ = 14
∴ x₂ = 12 and y₂ = 14
∴ Q(12, 14)
PQ = QR …[From (i)]
∴ Q is the midpoint of seg PR.
By midpoint formula,
12 = \(\large \frac {16\,+\,x₃}{2}\)
∴ 12 × 2 = 16 + x₃
∴ 24 = 16 + x₃
∴ 24 – 16 = x₃
∴ x₃ = 8
14 = \(\large \frac {12\,+\,y₃}{2}\)
∴ 14 × 2 = 12 + y₃
∴ 28 = 12 + y₃
∴ 28 – 12 = y₃
∴ y₃ = 16
∴ x₃ = 8 and y₃ = 16
∴ R(8, 16)
RS = BS …[From (i)]
∴ S is the midpoint of seg RB.
By midpoint formula,
x₄ = \(\large \frac {0\,+\,8}{2}\)
∴ x₄ = \(\large \frac {8}{2}\)
∴ x₄ = 4
y₄ = \(\large \frac {16\,+\,20}{2}\)
∴ y₄ = \(\large \frac {36}{2}\)
∴ y₄ = 18
∴ x₄ = 4 and y₄ = 18
∴ S(4, 18)
Ans: P (16, 12), Q (12, 14), R (8, 16) and S (4, 18) divides seg AB in five equal parts.
Practice set 5.3
1. Angles made by the line with the positive direction of X – axis are given. Find the slope of these lines.
(1) 45°
Solution:
Inclination of the line (θ) = 45⁰
Slope
= tan θ
= tan 45⁰
= 1
Ans: Slope = 1
(2) 60°
Solution:
Inclination of the line (θ) = 60⁰
Slope
= tan θ
= tan 60⁰
= \(\sqrt{3}\)
Ans: Slope = \(\sqrt{3}\)
(3) 90°
Solution:
Inclination of the line (θ) = 90⁰
Slope
= tan θ
= tan 90⁰
= Not Defined
Ans: Slope = Not Defined
2. Find the slopes of the lines passing through the given points.
(1) A (2, 3) , B (4, 7)
Solution:
A(2, 3) = (x₁, y₁)
B(4, 7) = (x₂, y₂)
Slope = \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
∴ Slope = \(\large \frac {7\,–\,3}{4\,–\,2}\)
∴ Slope = \(\large \frac {4}{2}\)
∴ Slope = 2
Ans: Slope of line AB = 2
(2) P (– 3, 1) , Q (5, – 2)
Solution:
P (– 3, 1) = (x₁, y₁)
Q (5, – 2) = (x₂, y₂)
Slope = \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
∴ Slope = \(\large \frac {–\,2\,–\,1}{5\,–\,(–\,3)}\)
∴ Slope = \(\large \frac {–\,3}{5\,+\,3}\)
∴ Slope = \(\large \frac {–\,3}{8}\)
Ans: Slope of line PQ = \(\large \frac {–\,3}{8}\)
(3) C (5, – 2) , D (7, 3)
Solution:
C (5, – 2) = (x₁, y₁)
D (7, 3) = (x₂, y₂)
Slope = \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
∴ Slope = \(\large \frac {3\,–\,(–\,2)}{7\,–\,5}\)
∴ Slope = \(\large \frac {3\,+\,2}{2}\)
∴ Slope = \(\large \frac {5}{2}\)
Ans: Slope of line CD = \(\large \frac {5}{2}\)
(4) L (– 2, – 3) , M (– 6, – 8)
Solution:
L (– 2, – 3) = (x₁, y₁)
M (– 6, – 8) = (x₂, y₂)
Slope = \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
∴ Slope = \(\large \frac {–\,8\,–\,(–\,3)}{–\,6\,–\,(–\,2)}\)
∴ Slope = \(\large \frac {–\,8\,+\,3}{–\,6\,+\,2}\)
∴ Slope = \(\large \frac {–\,5}{–\,4}\)
∴ Slope = \(\large \frac {5}{4}\)
Ans: Slope of line LM = \(\large \frac {5}{4}\)
(5) E(– 4, – 2) , F (6, 3)
Solution:
E(– 4, – 2) = (x₁, y₁)
F (6, 3) = (x₂, y₂)
Slope = \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
∴ Slope = \(\large \frac {3\,–\,(–\,2)}{6\,–\,(–\,4)}\)
∴ Slope = \(\large \frac {3\,+\,2}{6\,+\,4}\)
∴ Slope = \(\large \frac {5}{10}\)
∴ Slope = \(\large \frac {1}{2}\)
Ans: Slope of line EF = \(\large \frac {1}{2}\)
(6) T (0, – 3) , S (0, 4)
Solution:
T (0, – 3) = (x₁, y₁)
S (0, 4) = (x₂, y₂)
Slope = \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
∴ Slope = \(\large \frac {4\,–\,(–\,3)}{0\,–\,0}\)
∴ Slope = \(\large \frac {4\,+\,3}{0}\)
∴ Slope = \(\large \frac {7}{0}\)
∴ Slope = Not Defined
Ans: Slope of line TS = Not Defined.
3. Determine whether the following points are collinear.
(1) A(– 1, – 1), B(0, 1), C(1, 3)
Solution:
A(–1, –1) = (x₁, y₁)
B(0, 1) = (x₂, y₂)
C(1, 3) = (x₃, y₃)
Slope of line AB
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {1\,–\,(–\,1)}{0\,–\,(–\,1)}\)
= \(\large \frac {1\,+\,1}{0\,+\,1}\)
= \(\large \frac {2}{1}\)
∴ Slope of line AB = 2
Slope of line BC
= \(\large \frac {y₃\,–\,y₂}{x₃\,–\,x₂}\)
= \(\large \frac {3\,–\,1}{1\,–\,0}\)
= \(\large \frac {2}{1}\)
∴ Slope of line BC = 2
∴ Slope of line AB = Slope of line BC …[From (i) and (ii)]
Also, both lines have a common point B.
∴ Points A, B and C are collinear points.
(2) D(– 2, – 3), E(1, 0), F(2, 1)
Solution:
D(– 2, – 3) = (x₁, y₁)
E(1, 0) = (x₂, y₂)
F(2, 1) = (x₃, y₃)
Slope of line DE
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {0\,–\,(–\,3)}{1\,–\,(–\,2)}\)
= \(\large \frac {0\,+\,3}{1\,+\,2}\)
= \(\large \frac {3}{3}\)
∴ Slope of line DE = 1
Slope of line EF
= \(\large \frac {y₃\,–\,y₂}{x₃\,–\,x₂}\)
= \(\large \frac {1\,–\,0}{2\,–\,1}\)
= \(\large \frac {1}{1}\)
∴ Slope of line EF = 1
∴ Slope of line DE = Slope of line EF …[From (i) and (ii)]
Also, both lines have a common point E.
∴ Points D, E and F are collinear points.
(3) L(2, 5), M(3, 3), N(5, 1)
Solution:
L(2, 5) = (x₁, y₁)
M(3, 3) = (x₂, y₂)
N(5, 1) = (x₃, y₃)
Slope of line LM
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {3\,–\,5}{3\,–\,2}\)
= \(\large \frac {–\,2}{1}\)
∴ Slope of line LM = – 2
Slope of line MN
= \(\large \frac {y₃\,–\,y₂}{x₃\,–\,x₂}\)
= \(\large \frac {1\,–\,3}{5\,–\,3}\)
= \(\large \frac {–\,2}{2}\)
∴ Slope of line MN = – 1
∴ Slope of line LM ≠ Slope of line MN …[From (i) and (ii)]
∴ Points L, M and N are non-collinear points.
(4) P(2, – 5), Q(1, – 3), R(– 2, 3)
Solution:
P(2, – 5) = (x₁, y₁)
Q(1, – 3) = (x₂, y₂)
R(– 2, 3) = (x₃, y₃)
Slope of line PQ
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {–\,3\,–\,(–\,5)}{1\,–\,2}\)
= \(\large \frac {–\,3\,+\,5}{–\,1}\)
= \(\large \frac {2}{–\,1}\)
∴ Slope of line PQ = – 2
Slope of line QR
= \(\large \frac {y₃\,–\,y₂}{x₃\,–\,x₂}\)
= \(\large \frac {3\,–\,(–\,3)}{–\,2\,–\,1}\)
= \(\large \frac {3\,+\,3}{–\,3}\)
= \(\large \frac {6}{–\,3}\)
∴ Slope of line QR = – 2
∴ Slope of line PQ = Slope of line QR …[From (i) and (ii)]
Also, both lines have a common point Q.
∴ Points P, Q and R are collinear points.
(5) R(1, – 4), S(– 2, 2), T(– 3, 4)
Solution:
R(1, – 4) = (x₁, y₁)
S(– 2, 2) = (x₂, y₂)
T(– 3, 4) = (x₃, y₃)
Slope of line RS
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {2\,–\,(–\,4)}{–\,2\,–\,1}\)
= \(\large \frac {2\,+\,4}{–\,3}\)
= \(\large \frac {6}{–\,3}\)
∴ Slope of line RS = – 2
Slope of line SR
= \(\large \frac {y₃\,–\,y₂}{x₃\,–\,x₂}\)
= \(\large \frac {4\,–\,2}{–\,3\,–\,(–\,2)}\)
= \(\large \frac {2}{–\,3\,+\,2}\)
= \(\large \frac {2}{–\,1}\)
∴ Slope of line QR = – 2
∴ Slope of line RS = Slope of line ST …[From (i) and (ii)]
Also, they have a common point S.
∴ Points R, S and T are collinear points.
(6) A(– 4, 4), K(– 2, \(\large \frac {5}{2})\), N(4, – 2)
Solution:
A(– 4, 4) = (x₁, y₁)
K(– 2, \(\large \frac {5}{2})\) = (x₂, y₂)
N(4, – 2) = (x₃, y₃)
Slope of line AK
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {\frac{5}{2}\,–\,4}{–\,2\,–\,(–\,4)}\)
= \(\large \frac {\frac{5\,–\,8}{2}}{–\,2\,+\,4}\)
= \(\large \frac {\frac{–\,3}{2}}{2}\)
= \(\large \frac {–\,3}{2\,×\,2}\)
∴ Slope of line RS = \(\large \frac {–\,3}{4}\)
Slope of line AN
= \(\large \frac {y₃\,–\,y₂}{x₃\,–\,x₂}\)
= \(\large \frac {–\,2\,–\,4}{4\,–\,(–\,4)}\)
= \(\large \frac {–\,6}{4\,+\,4}\)
= \(\large \frac {–\,6}{8}\)
∴ Slope of line AN = \(\large \frac {–\,3}{4}\)
Slope of line AK = Slope of line AN …[From (i) and (ii)]
Also, they have a common point A.
∴ Points A, K and N are collinear points.
4. If A (1, – 1),B (0, 4),C (– 5, 3) are vertices of a triangle then find the slope of each side.
Solution:
A(1, –1), B(0, 4), C(–5, 3)
By using slope formula,
Slope of AB
= \(\large \frac {4\,–\,(–\,1)}{0\,–\,1}\)
= \(\large \frac {4\,+\,1}{–\,1}\)
= \(\large \frac {5}{–\,1}\)
∴ Slope of AB = – 5
Slope of BC
= \(\large \frac {3\,–\,4}{–\,5\,–\,0}\)
= \(\large \frac {–\,1}{–\,5}\)
∴ Slope of BC = \(\large \frac {1}{5}\)
Slope of AC
= \(\large \frac {3\,–\,(–\,1)}{–\,5\,–\,1}\)
= \(\large \frac {3\,+\,1}{–\,6}\)
= \(\large \frac {4}{–\,6}\)
∴ Slope of AC = \(\large \frac {–\,2}{3}\)
5. Show that A (– 4, – 7),B (– 1, 2), C (8, 5) and D (5, – 4) are the vertices of a parallelogram.
Solution:
A (– 4, – 7),B (– 1, 2), C (8, 5) and D (5, – 4)
By using slope formula,
Slope of AB
= \(\large \frac {2\,–\,(–\,7)}{–\,1\,–\,(–\,4)}\)
= \(\large \frac {2\,+\,7}{–\,1\,+\,4}\)
= \(\large \frac {9}{3}\)
∴ Slope of AB = 3
Slope of BC
= \(\large \frac {5\,–\,2}{8\,–\,(–\,1)}\)
= \(\large \frac {3}{8\,+\,1}\)
= \(\large \frac {3}{9}\)
∴ Slope of BC = \(\large \frac {1}{3}\)
Slope of AD
= \(\large \frac {–\,4\,–\,(–\,7)}{5\,–\,(–\,4)}\)
= \(\large \frac {–\,4\,+\,7}{5\,+\,4}\)
= \(\large \frac {3}{9}\)
∴ Slope of AD = \(\large \frac {1}{3}\)
Slope of CD
= \(\large \frac {–\,4\,–\,5}{5\,–\,8}\)
= \(\large \frac {–\,9}{–\,3}\)
= \(\large \frac {9}{3}\)
∴ Slope of CD = 3
Slope of line AB = Slope of line CD …[From (i) and (iv)]
∴ Line AB || Line CD …(v)
∴ Slope of line BC = Slope of line AD …[From (ii) and (iii)]
∴ Line BC || Line AD …(vi)
In □ ABCD,
AB || CD …[From (v)]
BC || AD …[From (vi)]
∴ □ ABCD is a parallelogram …[Definition]
6. Find k, if R(1, – 1), S (– 2, k) and slope of line RS is – 2.
Solution:
R(1, – 1) = (x₁, y₁)
S(– 2, k) = (x₂, y₂)
Slope of line RS = \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
∴ – 2 = \(\large \frac {k\,–\,(–\,1)}{–\,2\,–\,1}\)
∴ – 2 = \(\large \frac {k\,+\,1}{–\,3}\)
∴ – 2 × – 3 = k + 1
∴ k + 1 = 6
∴ k = 6 – 1
∴ k = 5
Ans: The value of k is 5.
7. Find k, if B(k, – 5), C (1, 2) and slope of the line is 7.
Solution:
B(k, –5) = (x₁, y₁)
C(1, 2) = (x₂, y₂)
Slope of line BC = \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
∴ 7 = \(\large \frac {2\,–\,(–\,5)}{1\,–\,k}\)
∴ 7(1 – k) = 2 + 5
∴ 7(1 – k) = 7
∴ 1 – k = \(\large \frac {7}{7}\)
∴ 1 – k = 1
∴ 1 – 1 = k
∴ k = 0
Ans: The value of k is 0.
8. Find k, if PQ || RS and P(2, 4), Q (3, 6), R(3, 1), S(5, k).
Solution:
Line PQ Line RS …[Given]
∴ Slope of line PQ = Slope of line RS
∴ \(\large \frac {6\,–\,4}{3\,–\,2}\) = \(\large \frac {k\,–\,1}{5\,–\,3}\)
∴ \(\large \frac {2}{1}\) = \(\large \frac {k\,–\,1}{2}\)
∴ 2 × 2 = k – 1
∴ 4 = k – 1
∴ 4 + 1 = k
∴ k = 5
Ans: The value of k is 5.
Problem Set 5
1. Fill in the blanks using correct alternatives.
(1) Seg AB is parallel to Y – axis and coordinates of point A are (1, 3) then co– ordinates of point B can be ______.
(A) (3, 1)
(B) (5, 3)
(C) (3, 0)
(D) (1, – 3)
Ans: Option (D) : (1, – 3)
(2) Out of the following, point …….. lies to the right of the origin on X– axis.
(A) (– 2, 0)
(B) (0, 2)
(C) (2, 3)
(D) (2, 0)
Ans: Option (D) : (2, 0)
(3) Distance of point (– 3, 4) from the origin is _____.
(A) 7
(B) 1
(C) 5
(D) – 5
Ans: Option (C) : 5
(4) A line makes an angle of 30° with the positive direction of the X – axis. So the slope of the line is ______.
(A) \(\large \frac {1}{2}\)
(B) \(\large \frac {\sqrt{3}}{2}\)
(C) \(\large \frac {1}{\sqrt{3}}\)
(D) \(\sqrt{3}\)
Ans: Option (C) : \(\large \frac {1}{\sqrt{3}}\)
2. Determine whether the given points are collinear.
(1) A(0, 2), B(1, – 0. 5), C(2, – 3)
Solution:
A(0, 2) = (x₁, y₁)
B(1, – 0. 5) = (x₂, y₂)
C(2, – 3) = (x₃, y₃)
Slope of line AB
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {–\,0.5\,–\,2}{1\,–\,0}\)
= \(\large \frac {–\,2.5}{1}\)
∴ Slope of line AB = – 2.5 …(i)
Slope of line AC
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {–\,3\,–\,(–\,0.5)}{2\,–\,1}\)
= \(\large \frac {–\,3\,+\,0.5}{1}\)
∴ Slope of line AC = – 2.5 …(ii)
∴ Slope of line AB = Slope of line AC …[From (i) and (ii)]
Also, they have a common point A.
∴ Points A, B and C are collinear points.
(2) P(1, 2), Q(2, \(\large \frac {8}{5})\), R(3, \(\large \frac {6}{5}\)
Solution:
P(1, 2) = (x₁, y₁)
Q(2, \(\large \frac {8}{5})\) = (x₂, y₂)
R(3, \(\large \frac {6}{5}\) = (x₃, y₃)
Slope of line PQ
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {\frac {8}{5}\,–\,2}{2\,–\,1}\)
= \(\large \frac {\frac {8\,–\,10}{5}}{1}\)
∴ Slope of line AB = \(\large \frac {–\,2}{5}\) …(i)
Slope of line QR
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {\frac {6}{5}\,–\,\frac {8}{5}}{3\,–\,2}\)
= \(\large \frac {\frac {–\,2}{5}}{1}\)
∴ Slope of line AC = \(\large \frac {–\,2}{5}\) …(ii)
∴ Slope of line PQ = Slope of line QR …[From (i) and (ii)]
Also, they have a common point Q.
∴ Points P, Q and R are collinear points.
(3) L(1, 2), M(5, 3), N(8, 6)
Solution:
L(1, 2) = (x₁, y₁)
M(5, 3) = (x₂, y₂)
N(8, 6) = (x₃, y₃)
Slope of line LM
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {3\,–\,2}{5\,–\,1}\)
∴ Slope of line LM = \(\large \frac {1}{4}\) …(i)
Slope of line MN
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {6\,–\,3}{8\,–\,5}\)
= \(\large \frac {3}{3}\)
∴ Slope of line MN = 1 …(ii)
∴ Slope of line LM ≠ Slope of line MN …[From (i) and (ii)]
∴ Points L, M and N are not collinear points.
3. Find the coordinates of the midpoint of the line segment joining P(0, 6) and Q(12, 20).
Solution:
P(0, 6) = (x₁, y₁) and Q(12, 20) = (x₂, y₂)
Let M (x, y) be the midpoint of seg PQ.
By midpoint formula,
x = \(\large \frac {x₁\,+\,x₂}{2}\)
∴ x = \(\large \frac {0\,+\,12}{2}\)
∴ x = \(\large \frac {12}{2}\)
∴ x = 6
y = \(\large \frac {y₁\,+\,y₂}{2}\)
∴ y = \(\large \frac {6\,+\,20}{2}\)
∴ y = \(\large \frac {26}{2}\)
∴ y = 13
Ans: M(6, 13) is the midpoint of segment joining P (0, 6) and Q (12, 20)
4. Find the ratio in which the line segment joining the points A(3, 8) and B(– 9, 3) is divided by the Y – axis.
Solution:
A(3, 8) = (x₁, y₁)
B(– 9, 3) = (x₂, y₂)
Let point P(0, a) be a point on the Y-axis which divides seg AB in the ratio m : n.
P(0, a) = (x, y)
By Section formula,
x = \(\large \frac {mx₂\,+\,nx₁}{m\,+\,n}\)
∴ 0 = \(\large \frac {m(–\,9)\,+\,n(3)}{m\,+\,n}\)
∴ 0 × (m + n) = – 9m + 3n
∴ 0 = – 9m + 3n
∴ 9m = 3n
∴ \(\large \frac {m}{n}\) = \(\large \frac {3}{9}\)
∴ \(\large \frac {m}{n}\) = \(\large \frac {1}{3}\)
∴ m : n = 1 : 3
Ans: Y-axis divides segment joining points A and B in the ratios 1 : 3.
5. Find the point on the X – axis which is equidistant from P(2, – 5) and Q(– 2, 9).
Solution:
Let A(a, 0) be a point equidistant from P(2, – 5) and Q(– 2, 9).
∴ d(P, A) = d(Q, A)
Using distance formula,
\(\sqrt{(a\,–\,2)²\,+\,[0\,–\,(–\,5)]²}\) = \(\sqrt{[a\,–\,(–\,2)]²\,+\,(0\,–\,9)²}\)
Squaring both the sides we get,
(a – 2)² + 5² = (a + 2)² + (– 9)²
∴ a² – 4a + 4 + 25 = a² + 4a + 4 + 81
∴ a² – 4a – a² – 4a = 81 – 25
∴ – 8a = 56
∴ a = \(\large \frac {56}{–\,8}\)
∴ a = – 7
Ans: (– 7, 0) is a point on the X-axis equidistant from P(2, – 5) and Q(– 2, 9).
6. Find the distances between the following points.
(i) A(a, 0), B(0, a)
Solution:
Let A(a, 0) = (x₁, y₁)
B(0, a) = (x₂, y₂)
By distance formula,
d(A, B) = \(\sqrt{(x₂\,–\,x₁)^2\,+\,(y₂\,–\,y₁)^2}\)
∴ d(A, B) = \(\sqrt{(0\,–\,a)^2\,+\,(a\,–\,0)^2}\)
∴ d(A, B) = \(\sqrt{(–\,a)^2\,+\,(a)^2}\)
∴ d(A, B) = \(\sqrt{a²\,+\,a²}\)
∴ d(A, B) = \(\sqrt{2(a²)}\)
∴ d(A, B) = \(\sqrt{2}\)a units
Ans: d(A, B) = \(\sqrt{2}\)a units
(ii) P(– 6, – 3), Q(– 1, 9)
Solution:
Let P(– 6, – 3) = (x₁, y₁)
Q(– 1, 9) = (x₂, y₂)
By distance formula,
d(P, Q) = \(\sqrt{(x₂\,–\,x₁)^2\,+\,(y₂\,–\,y₁)^2}\)
∴ d(P, Q) = \(\sqrt{[–\,1\,–\,(–\,6)^2\,+\,[9\,–\,(–\,3)^2}\)
∴ d(P, Q) = \(\sqrt{(–\,1\,+\,6)^2\,+\,(9\,+\,3)^2}\)
∴ d(P, Q) = \(\sqrt{(5)^2\,+\,(12)^2}\)
∴ d(P, Q) = \(\sqrt{25\,+\,143}\)
∴ d(P, Q) = \(\sqrt{169}\)
∴ d(P, Q) = 13 units
Ans: d(P, Q) = 13 units
(iii) R(– 3a, a), S(a, – 2a)
Solution:
Let R(– 3a, a) = (x₁, y₁)
S(a, – 2a) = (x₂, y₂)
By distance formula,
d(R, S) = \(\sqrt{(x₂\,–\,x₁)^2\,+\,(y₂\,–\,y₁)^2}\)
∴ d(R, S) = \(\sqrt{[a\,–\,(–\,3a)]^2\,+\,(–\,2a\,–\,a)^2}\)
∴ d(R, S) = \(\sqrt{(a\,+\,3a)^2\,+\,(–\,3a)^2}\)
∴ d(R, S) = \(\sqrt{(4a)^2\,+\,9a²}\)
∴ d(R, S) = \(\sqrt{16a²\,+\,9a²}\)
∴ d(R, S) = \(\sqrt{25a²}\)
∴ d(R, S) = 5a units
Ans: d(R, S) = 5a units
(6) T (0, – 3) , S (0, 4)
Solution:
T (0, – 3) = (x₁, y₁)
S (0, 4) = (x₂, y₂)
Slope = \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
∴ Slope = \(\large \frac {4\,–\,(–\,3)}{0\,–\,0}\)
∴ Slope = \(\large \frac {4\,+\,3}{0}\)
∴ Slope = \(\large \frac {7}{0}\)
∴ Slope = Not Defined
Ans: Slope of line TS = Not Defined.
3. Determine whether the following points are collinear.
(1) A(– 1, – 1), B(0, 1), C(1, 3)
Solution:
A(–1, –1) = (x₁, y₁)
B(0, 1) = (x₂, y₂)
C(1, 3) = (x₃, y₃)
Slope of line AB
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {1\,–\,(–\,1)}{0\,–\,(–\,1)}\)
= \(\large \frac {1\,+\,1}{0\,+\,1}\)
= \(\large \frac {2}{1}\)
∴ Slope of line AB = 2
Slope of line BC
= \(\large \frac {y₃\,–\,y₂}{x₃\,–\,x₂}\)
= \(\large \frac {3\,–\,1}{1\,–\,0}\)
= \(\large \frac {2}{1}\)
∴ Slope of line BC = 2
∴ Slope of line AB = Slope of line BC …[From (i) and (ii)]
Also, both lines have a common point B.
∴ Points A, B and C are collinear points.
(2) D(– 2, – 3), E(1, 0), F(2, 1)
Solution:
D(– 2, – 3) = (x₁, y₁)
E(1, 0) = (x₂, y₂)
F(2, 1) = (x₃, y₃)
Slope of line DE
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {0\,–\,(–\,3)}{1\,–\,(–\,2)}\)
= \(\large \frac {0\,+\,3}{1\,+\,2}\)
= \(\large \frac {3}{3}\)
∴ Slope of line DE = 1
Slope of line EF
= \(\large \frac {y₃\,–\,y₂}{x₃\,–\,x₂}\)
= \(\large \frac {1\,–\,0}{2\,–\,1}\)
= \(\large \frac {1}{1}\)
∴ Slope of line EF = 1
∴ Slope of line DE = Slope of line EF …[From (i) and (ii)]
Also, both lines have a common point E.
∴ Points D, E and F are collinear points.
(3) L(2, 5), M(3, 3), N(5, 1)
Solution:
L(2, 5) = (x₁, y₁)
M(3, 3) = (x₂, y₂)
N(5, 1) = (x₃, y₃)
Slope of line LM
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {3\,–\,5}{3\,–\,2}\)
= \(\large \frac {–\,2}{1}\)
∴ Slope of line LM = – 2
Slope of line MN
= \(\large \frac {y₃\,–\,y₂}{x₃\,–\,x₂}\)
= \(\large \frac {1\,–\,3}{5\,–\,3}\)
= \(\large \frac {–\,2}{2}\)
∴ Slope of line MN = – 1
∴ Slope of line LM ≠ Slope of line MN …[From (i) and (ii)]
∴ Points L, M and N are non-collinear points.
(4) P(2, – 5), Q(1, – 3), R(– 2, 3)
Solution:
P(2, – 5) = (x₁, y₁)
Q(1, – 3) = (x₂, y₂)
R(– 2, 3) = (x₃, y₃)
Slope of line PQ
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {–\,3\,–\,(–\,5)}{1\,–\,2}\)
= \(\large \frac {–\,3\,+\,5}{–\,1}\)
= \(\large \frac {2}{–\,1}\)
∴ Slope of line PQ = – 2
Slope of line QR
= \(\large \frac {y₃\,–\,y₂}{x₃\,–\,x₂}\)
= \(\large \frac {3\,–\,(–\,3)}{–\,2\,–\,1}\)
= \(\large \frac {3\,+\,3}{–\,3}\)
= \(\large \frac {6}{–\,3}\)
∴ Slope of line QR = – 2
∴ Slope of line PQ = Slope of line QR …[From (i) and (ii)]
Also, both lines have a common point Q.
∴ Points P, Q and R are collinear points.
(5) R(1, – 4), S(– 2, 2), T(– 3, 4)
Solution:
R(1, – 4) = (x₁, y₁)
S(– 2, 2) = (x₂, y₂)
T(– 3, 4) = (x₃, y₃)
Slope of line RS
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {2\,–\,(–\,4)}{–\,2\,–\,1}\)
= \(\large \frac {2\,+\,4}{–\,3}\)
= \(\large \frac {6}{–\,3}\)
∴ Slope of line RS = – 2
Slope of line SR
= \(\large \frac {y₃\,–\,y₂}{x₃\,–\,x₂}\)
= \(\large \frac {4\,–\,2}{–\,3\,–\,(–\,2)}\)
= \(\large \frac {2}{–\,3\,+\,2}\)
= \(\large \frac {2}{–\,1}\)
∴ Slope of line QR = – 2
∴ Slope of line RS = Slope of line ST …[From (i) and (ii)]
Also, they have a common point S.
∴ Points R, S and T are collinear points.
(6) A(– 4, 4), K(– 2, \(\large \frac {5}{2})\), N(4, – 2)
Solution:
A(– 4, 4) = (x₁, y₁)
K(– 2, \(\large \frac {5}{2})\) = (x₂, y₂)
N(4, – 2) = (x₃, y₃)
Slope of line AK
= \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
= \(\large \frac {\frac{5}{2}\,–\,4}{–\,2\,–\,(–\,4)}\)
= \(\large \frac {\frac{5\,–\,8}{2}}{–\,2\,+\,4}\)
= \(\large \frac {\frac{–\,3}{2}}{2}\)
= \(\large \frac {–\,3}{2\,×\,2}\)
∴ Slope of line RS = \(\large \frac {–\,3}{4}\)
Slope of line AN
= \(\large \frac {y₃\,–\,y₂}{x₃\,–\,x₂}\)
= \(\large \frac {–\,2\,–\,4}{4\,–\,(–\,4)}\)
= \(\large \frac {–\,6}{4\,+\,4}\)
= \(\large \frac {–\,6}{8}\)
∴ Slope of line AN = \(\large \frac {–\,3}{4}\)
Slope of line AK = Slope of line AN …[From (i) and (ii)]
Also, they have a common point A.
∴ Points A, K and N are collinear points.
4. If A (1, – 1),B (0, 4),C (– 5, 3) are vertices of a triangle then find the slope of each side.
Solution:
A(1, –1), B(0, 4), C(–5, 3)
By using slope formula,
Slope of AB
= \(\large \frac {4\,–\,(–\,1)}{0\,–\,1}\)
= \(\large \frac {4\,+\,1}{–\,1}\)
= \(\large \frac {5}{–\,1}\)
∴ Slope of AB = – 5
Slope of BC
= \(\large \frac {3\,–\,4}{–\,5\,–\,0}\)
= \(\large \frac {–\,1}{–\,5}\)
∴ Slope of BC = \(\large \frac {1}{5}\)
Slope of AC
= \(\large \frac {3\,–\,(–\,1)}{–\,5\,–\,1}\)
= \(\large \frac {3\,+\,1}{–\,6}\)
= \(\large \frac {4}{–\,6}\)
∴ Slope of AC = \(\large \frac {–\,2}{3}\)
5. Show that A (– 4, – 7),B (– 1, 2), C (8, 5) and D (5, – 4) are the vertices of a parallelogram.
Solution:
A (– 4, – 7),B (– 1, 2), C (8, 5) and D (5, – 4)
By using slope formula,
Slope of AB
= \(\large \frac {2\,–\,(–\,7)}{–\,1\,–\,(–\,4)}\)
= \(\large \frac {2\,+\,7}{–\,1\,+\,4}\)
= \(\large \frac {9}{3}\)
∴ Slope of AB = 3
Slope of BC
= \(\large \frac {5\,–\,2}{8\,–\,(–\,1)}\)
= \(\large \frac {3}{8\,+\,1}\)
= \(\large \frac {3}{9}\)
∴ Slope of BC = \(\large \frac {1}{3}\)
Slope of AD
= \(\large \frac {–\,4\,–\,(–\,7)}{5\,–\,(–\,4)}\)
= \(\large \frac {–\,4\,+\,7}{5\,+\,4}\)
= \(\large \frac {3}{9}\)
∴ Slope of AD = \(\large \frac {1}{3}\)
Slope of CD
= \(\large \frac {–\,4\,–\,5}{5\,–\,8}\)
= \(\large \frac {–\,9}{–\,3}\)
= \(\large \frac {9}{3}\)
∴ Slope of CD = 3
Slope of line AB = Slope of line CD …[From (i) and (iv)]
∴ Line AB || Line CD …(v)
∴ Slope of line BC = Slope of line AD …[From (ii) and (iii)]
∴ Line BC || Line AD …(vi)
In □ ABCD,
AB || CD …[From (v)]
BC || AD …[From (vi)]
∴ □ ABCD is a parallelogram …[Definition]
6. Find k, if R(1, – 1), S (– 2, k) and slope of line RS is – 2.
Solution:
R(1, – 1) = (x₁, y₁)
S(– 2, k) = (x₂, y₂)
Slope of line RS = \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
∴ – 2 = \(\large \frac {k\,–\,(–\,1)}{–\,2\,–\,1}\)
∴ – 2 = \(\large \frac {k\,+\,1}{–\,3}\)
∴ – 2 × – 3 = k + 1
∴ k + 1 = 6
∴ k = 6 – 1
∴ k = 5
Ans: The value of k is 5.
7. Find k, if B(k, – 5), C (1, 2) and slope of the line is 7.
Solution:
B(k, –5) = (x₁, y₁)
C(1, 2) = (x₂, y₂)
Slope of line BC = \(\large \frac {y₂\,–\,y₁}{x₂\,–\,x₁}\)
∴ 7 = \(\large \frac {2\,–\,(–\,5)}{1\,–\,k}\)
∴ 7(1 – k) = 2 + 5
∴ 7(1 – k) = 7
∴ 1 – k = \(\large \frac {7}{7}\)
∴ 1 – k = 1
∴ 1 – 1 = k
∴ k = 0
Ans: The value of k is 0.
8. Find k, if PQ || RS and P(2, 4), Q (3, 6), R(3, 1), S(5, k).
Solution:
Line PQ Line RS …[Given]
∴ Slope of line PQ = Slope of line RS
∴ \(\large \frac {6\,–\,4}{3\,–\,2}\) = \(\large \frac {k\,–\,1}{5\,–\,3}\)
∴ \(\large \frac {2}{1}\) = \(\large \frac {k\,–\,1}{2}\)
∴ 2 × 2 = k – 1
∴ 4 = k – 1
∴ 4 + 1 = k
∴ k = 5
Ans: The value of k is 5.
