Chapter 4 – Geometric Constructions
Practice set 4.1
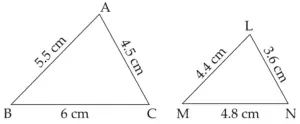
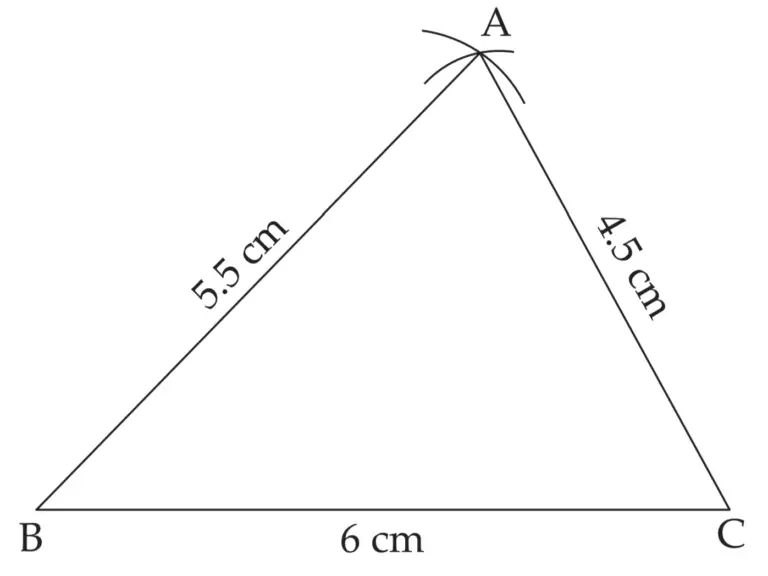
1. ∆ABC ~ ∆LMN. In ∆ABC, AB = 5.5 cm, BC = 6 cm, CA = 4.5 cm. Construct ∆ABC and DLMN such that \(\large \frac {BC}{MN}\) = \(\large \frac {5}{4}\)
Solution:
∆ABC ~ ∆LMN …[Given]
∴ \(\large \frac {AB}{LM}\) = \(\large \frac {BC}{MN}\) = \(\large \frac {AC}{LN}\) …(i) [c.s.c.t.]
Now,
\(\large \frac {BC}{MN}\) = \(\large \frac {5}{4}\) …(ii) [Given]
∴ \(\large \frac {AB}{LM}\) = \(\large \frac {BC}{MN}\) = \(\large \frac {AC}{LN}\) = \(\large \frac {5}{4}\) …[from (i) and (ii)]
∴ \(\large \frac {AB}{LM}\) = \(\large \frac {5}{4}\) ; \(\large \frac {BC}{MN}\) = \(\large \frac {5}{4}\) ; \(\large \frac {AC}{LN}\) = \(\large \frac {5}{4}\)
∴ \(\large \frac {5.5}{LM}\) = \(\large \frac {5}{4}\) ; \(\large \frac {6}{MN}\) = \(\large \frac {5}{4}\) ; \(\large \frac {4.5}{LN}\) = \(\large \frac {5}{4}\)
∴ LM = \(\large \frac {5.5\,×\,4}{5}\) ; MN = \(\large \frac {6\,×\,4}{5}\) ; LN = \(\large \frac {4.5\,×\,4}{5}\)
∴ LM = 4.4 cm , MN = 4.8 cm , LN = 3.6 cm
ROUGH FIGURE
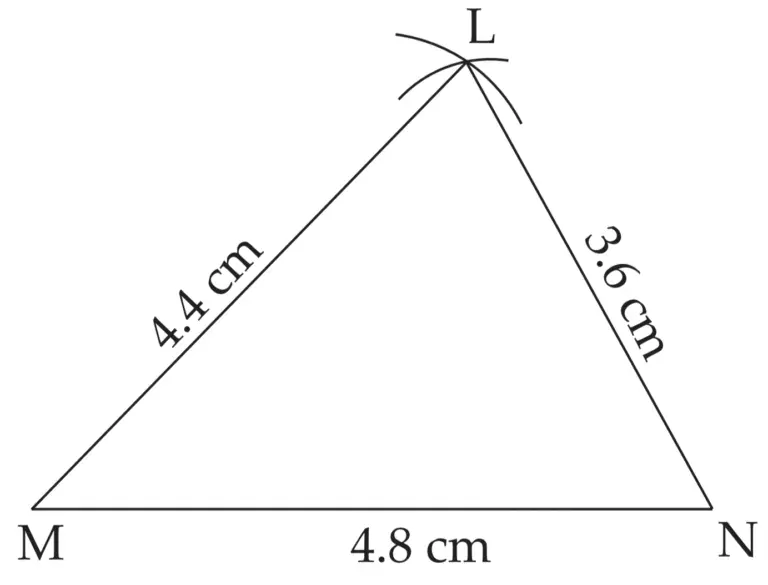
∆LMN is the required triangle similar to ∆ABC.
2. ∆PQR ~ ∆LTR. In ∆PQR, PQ = 4.2 cm, QR = 5.4 cm, PR = 4.8 cm. Construct ∆PQR and ∆LTR, such that \(\large \frac {PQ}{LT}\) = \(\large \frac {3}{4}\)
Solution:
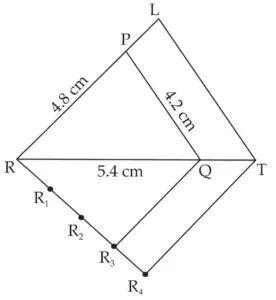
ROUGH FIGURE
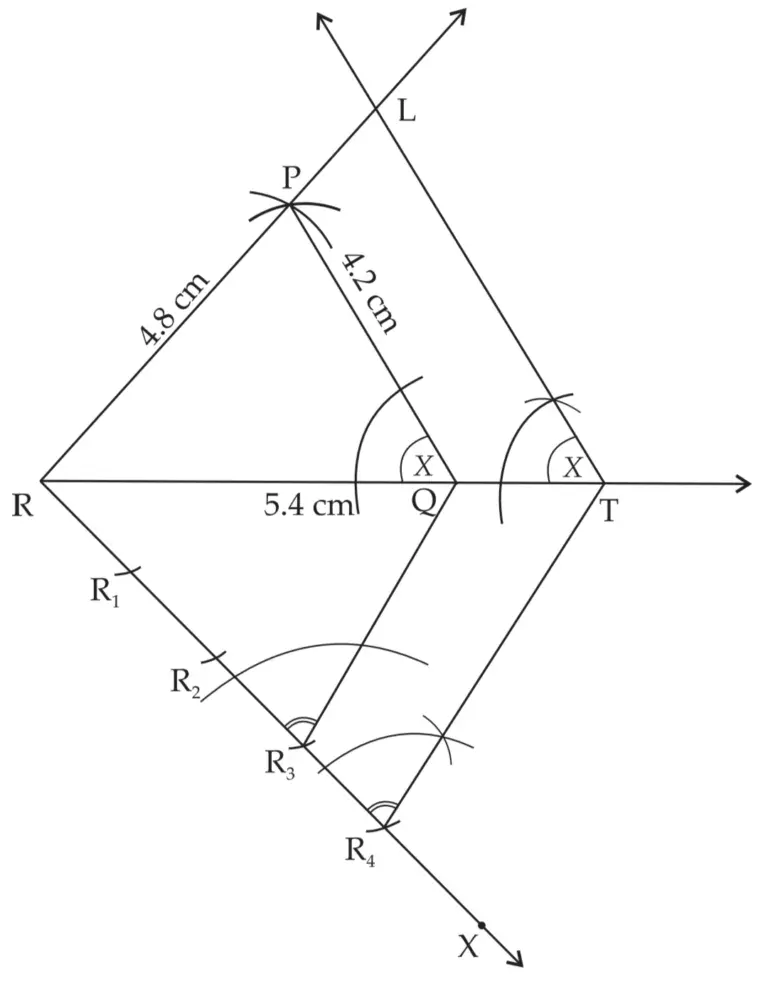
∆LTR is the required triangle similar to ∆PQR.
3. ∆RST ~ ∆XYZ. In ∆RST, RS = 4.5 cm, ∠RST = 40°, ST = 5.7 cm Construct ∆RST and ∆XYZ, such that \(\large \frac {RS}{XY}\) = \(\large \frac {3}{5}\).
Solution:
∆RST ~ ∆XYZ …[Given]
∠RST ≅ ∠XYZ …[c.a.s.t]
∵ ∠RST = 40° …[Given]
∴ ∠XYZ = 40° …(i)
∴ \(\large \frac {RS}{XY}\) = \(\large \frac {ST}{YZ}\) …(i) [c.s.s.t]
Now,
\(\large \frac {RS}{XY}\) = \(\large \frac {3}{5}\) …(ii) [Given]
∴ \(\large \frac {RS}{XY}\) = \(\large \frac {ST}{YZ}\) = \(\large \frac {3}{5}\) …[from (i) and (ii)]
∴ \(\large \frac {RS}{XY}\) = \(\large \frac {3}{5}\) ; \(\large \frac {ST}{YZ}\) = \(\large \frac {3}{5}\)
∴ \(\large \frac {4.5}{XY}\) = \(\large \frac {3}{5}\) ; \(\large \frac {5.7}{YZ}\) = \(\large \frac {3}{5}\)
∴ XY = \(\large \frac {4.55}{3}\) ; YZ = \(\large \frac {5.75}{3}\)
∴ XY = 7.5 cm, YZ = 9.5 cm
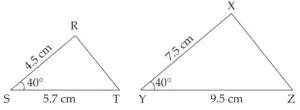
ROUGH FIGURE
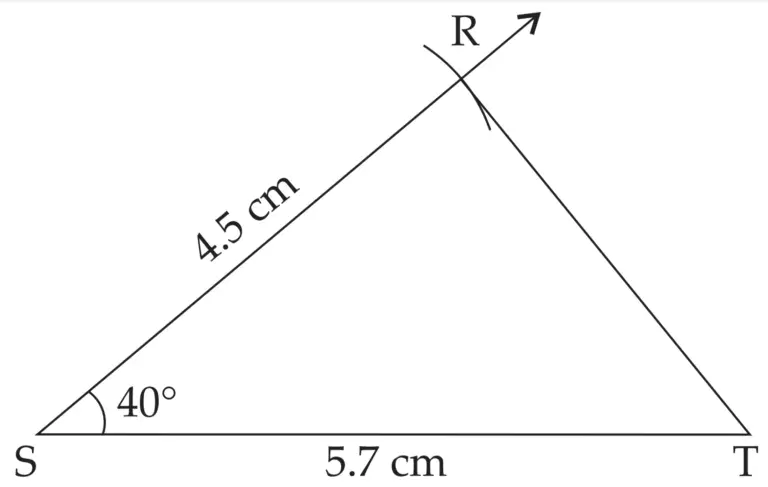
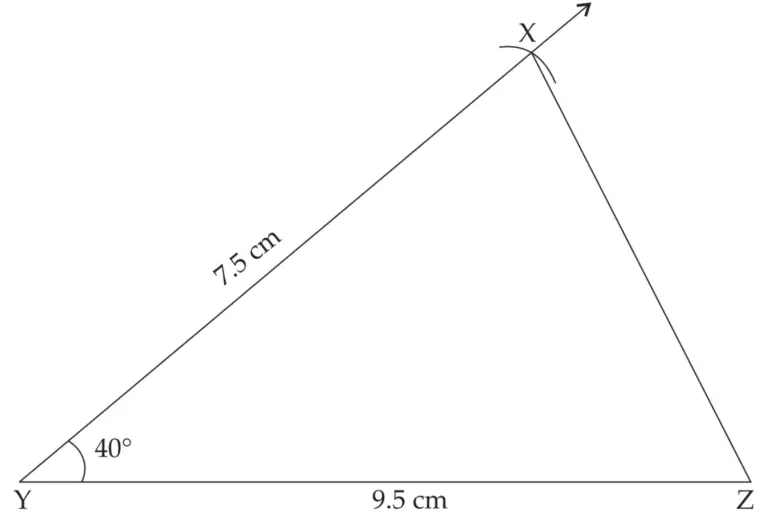
∆XYZ is the required triangle similar to ∆RST.
4. ∆AMT ~ ∆AHE. In ∆AMT, AM = 6.3 cm, ∠TAM = 50°, AT = 5.6 cm. \(\large \frac {AM}{AH}\) = \(\large \frac {7}{5}\). Construct ∆AHE.
Solution:
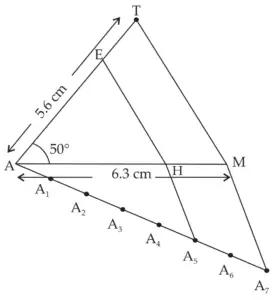
ROUGH FIGURE
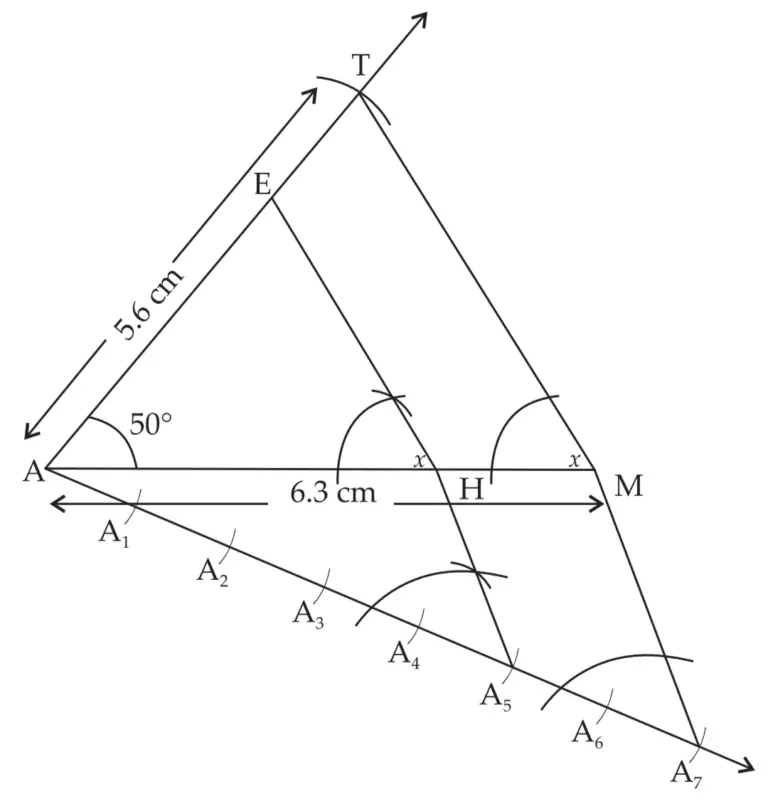
∆AHE is the required triangle similar to ∆AMT.
Practice set 4.2
1. Construct a tangent to a circle with centre P and radius 3.2 cm at any point M on it.
Solution:
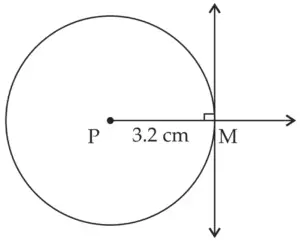
ROUGH FIGURE
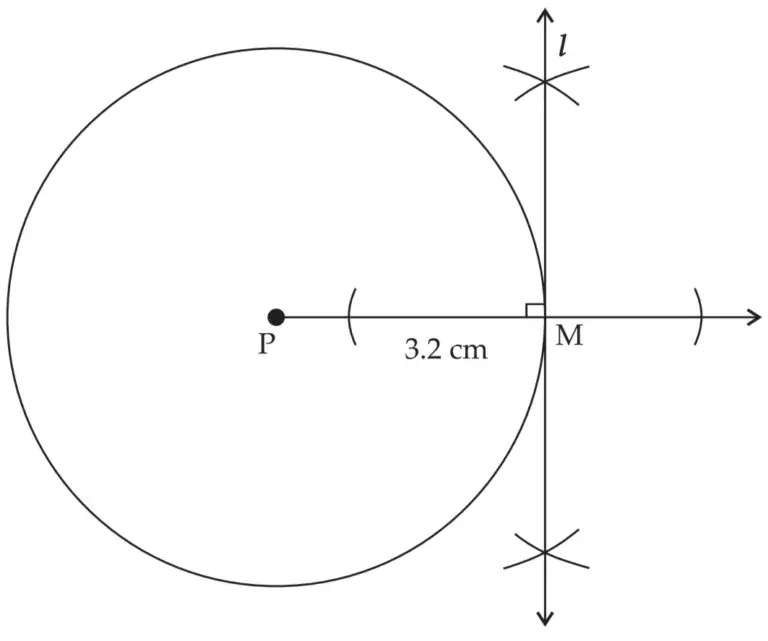
line l is the required tangent to the circle passing through point M on the circle.
2. Draw a circle of radius 2.7 cm. Draw a tangent to the circle at any point on it.
Solution:
ROUGH FIGURE
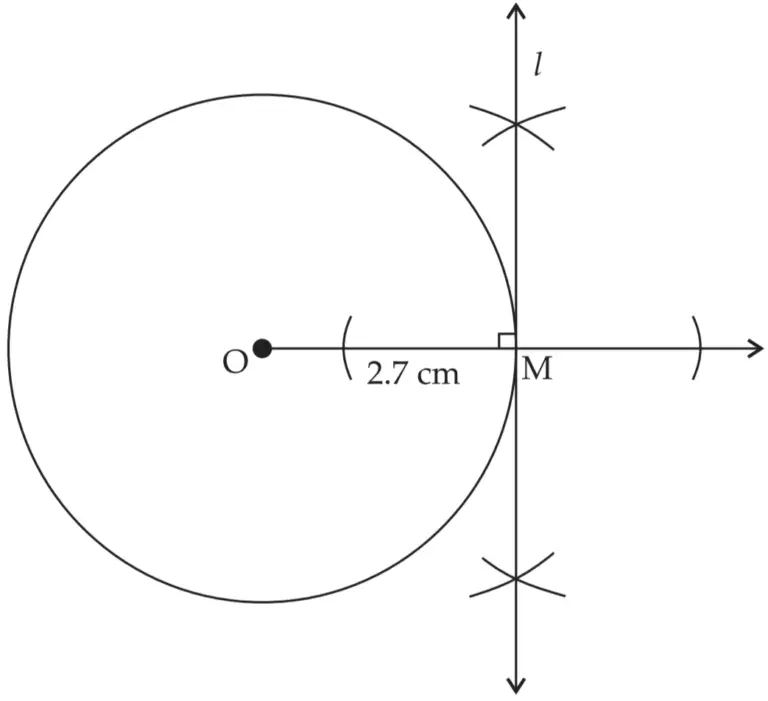
line l is the required tangent to the circle passing through point M on the circle.
3. Draw a circle of radius 3.6 cm. Draw a tangent to the circle at any point on it without using the centre.
Solution:
ROUGH FIGURE
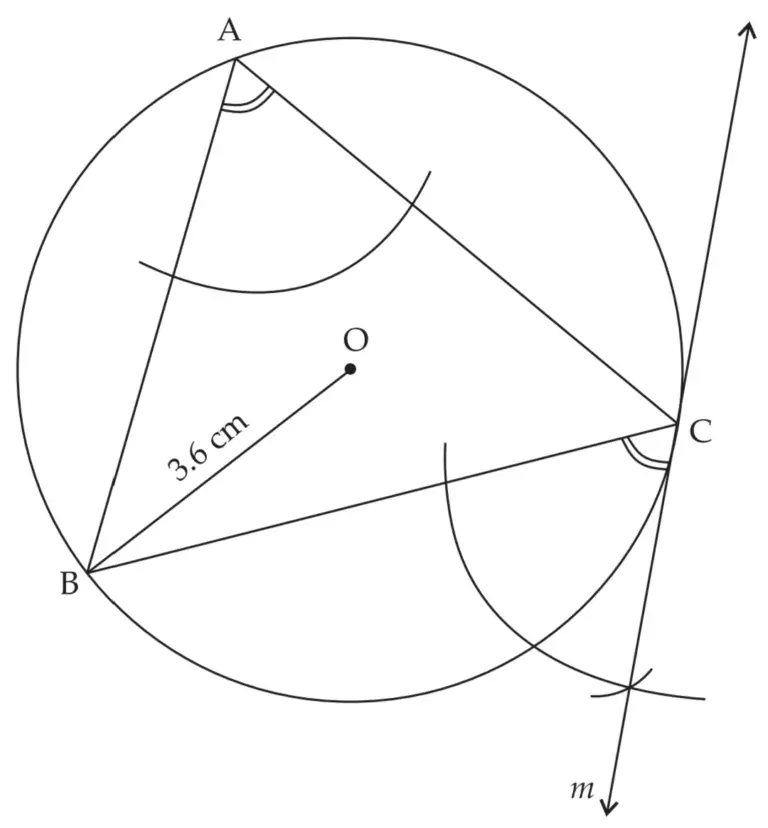
Line m is the required tangent to the circle at point C.
4. Draw a circle of radius 3.3 cm Draw a chord PQ of length 6.6 cm. Draw tangents to the circle at points P and Q. Write your observation about the tangents.
Solution:
Radius = 3.3 cm …[Given]
Chord = 6.6 cm …[Given]
Chord is twice the radius.
Chord PQ is a diameter.
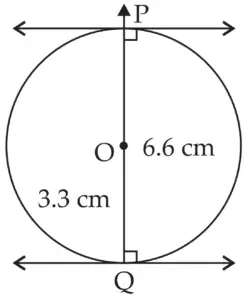
ROUGH FIGURE
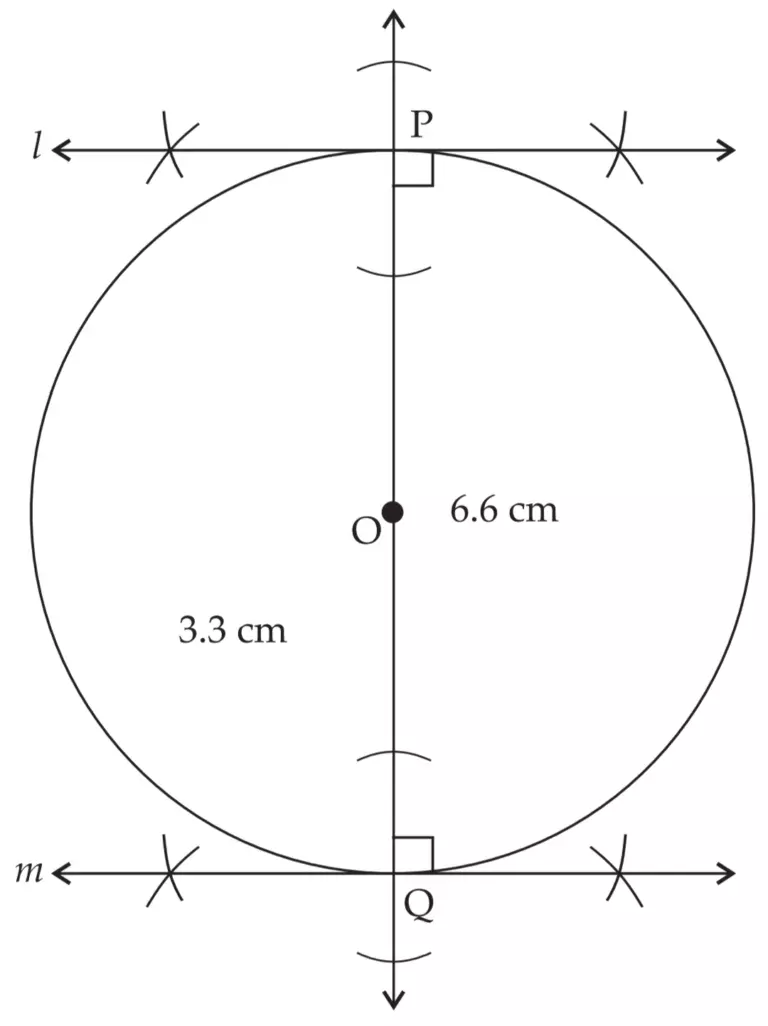
line l and m are the required tangents to the circle at point P and point Q.
Tangents at the end points of a diameter are parallel to each other.
5. Draw a circle with radius 3.4 cm. Draw a chord MN of length 5.7 cm in it. Construct tangents at point M and N to the circle.
Solution:
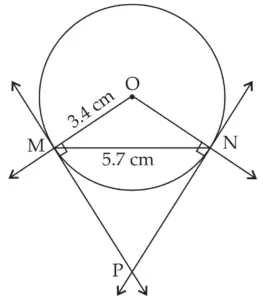
ROUGH FIGURE
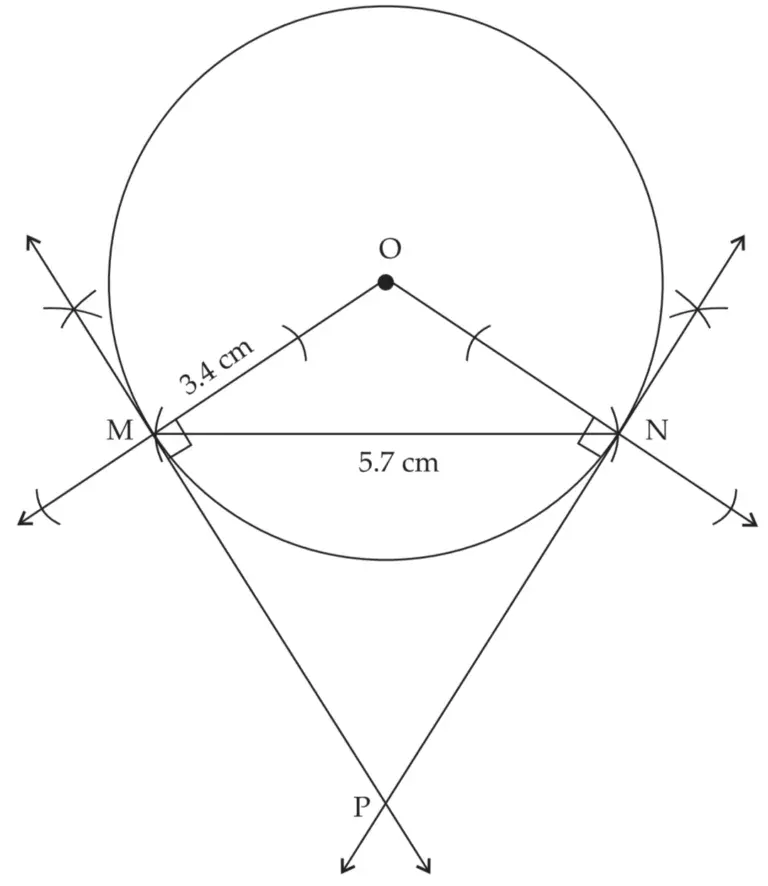
Line MP and line NP are required tangents to the circle at point M and point N respectively.
6. Draw a circle with centre P and radius 3.4 cm. Take point Q at a distance 5.5 cm from the centre. Construct tangents to the circle from point Q.
Solution:
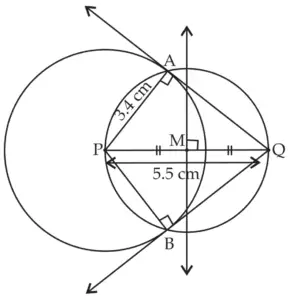
ROUGH FIGURE
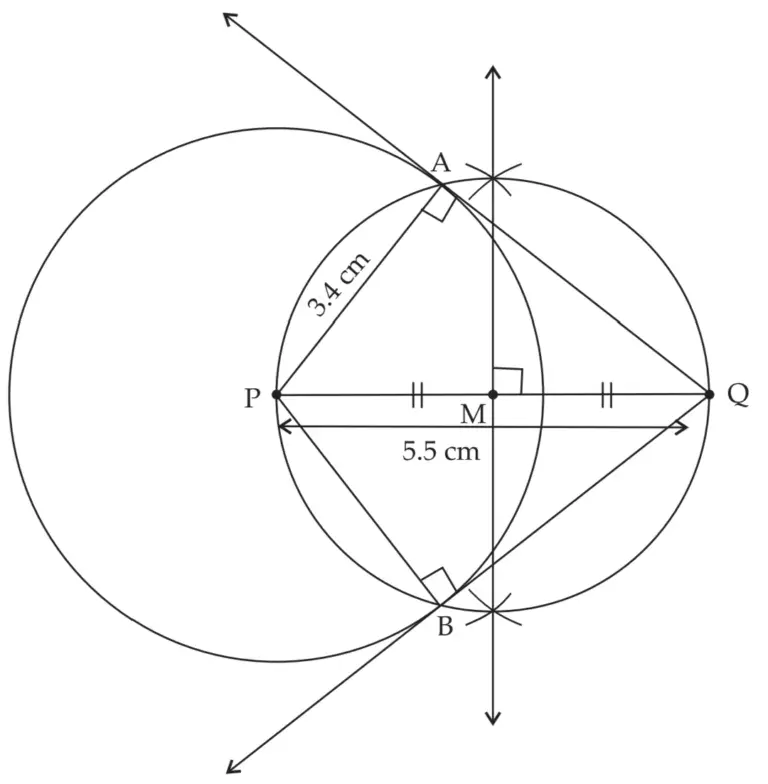
line MQ and line NQ are the required tangents to the circle from point Q.
7. Draw a circle with radius 4.1 cm. Construct tangents to the circle from a point at a distance 7.3 cm from the centre.
Solution:
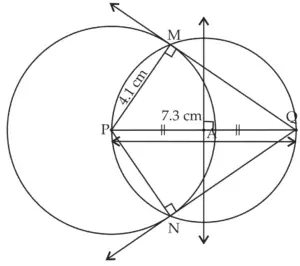
ROUGH FIGURE
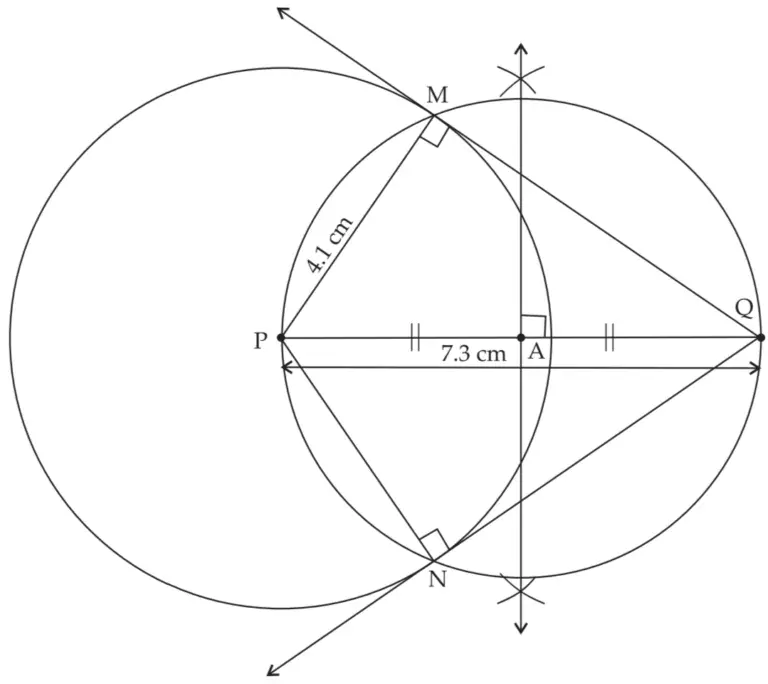
Line MQ and line NQ are the required tangents to the circle from point Q.
Problem set 4
1. Select the correct alternative for each of the following questions.
(1) The number of tangents that can be drawn to a circle at a point on the circle is ______.
(A) 3
(B) 2
(C) 1
(D) 0
Ans: Option (C) : 1
(2) The maximum number of tangents that can be drawn to a circle from a point outside it is ______.
(A) 2
(B) 1
(C) one and only one
(D) 0
Ans: Option (A) : 2
(3) If ∆ABC ~ ∆PQR and \(\large \frac {AB}{PQ}\) = \(\large \frac {7}{5}\), then ______.
(A) ∆ABC is bigger.
(B) ∆PQR is bigger.
(C) Both triangles will be equal.
(D) Can not be decided.
Ans: Option (A) : ∆ABC is bigger
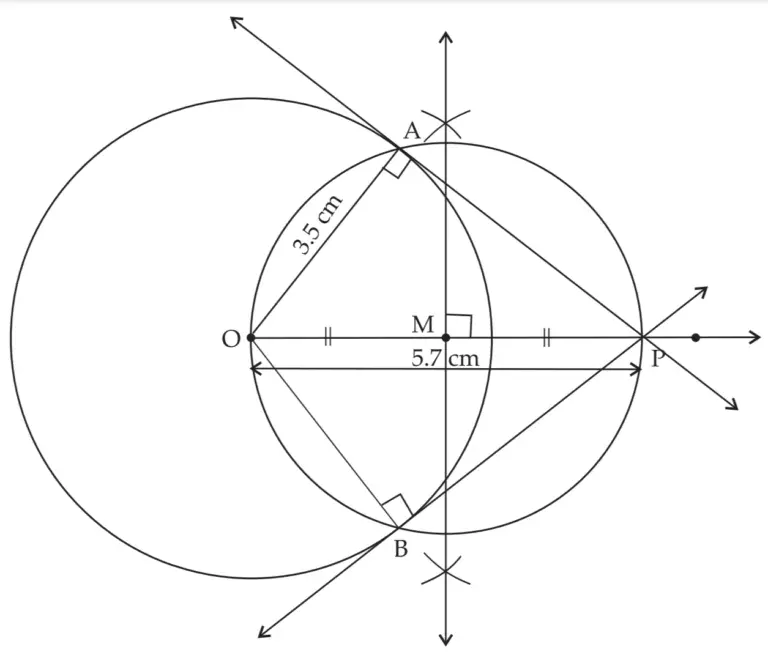
2. Draw a circle with centre O and radius 3.5 cm. Take point P at a distance 5.7 cm from the centre. Draw tangents to the circle from point P.
Solution:
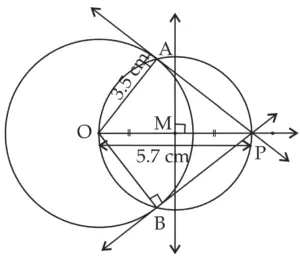
ROUGH FIGURE
3. Draw any circle. Take any point A on it and construct tangent at A without using the centre of the circle.
Solution:
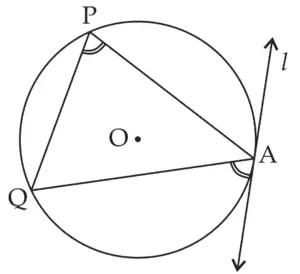
ROUGH FIGURE
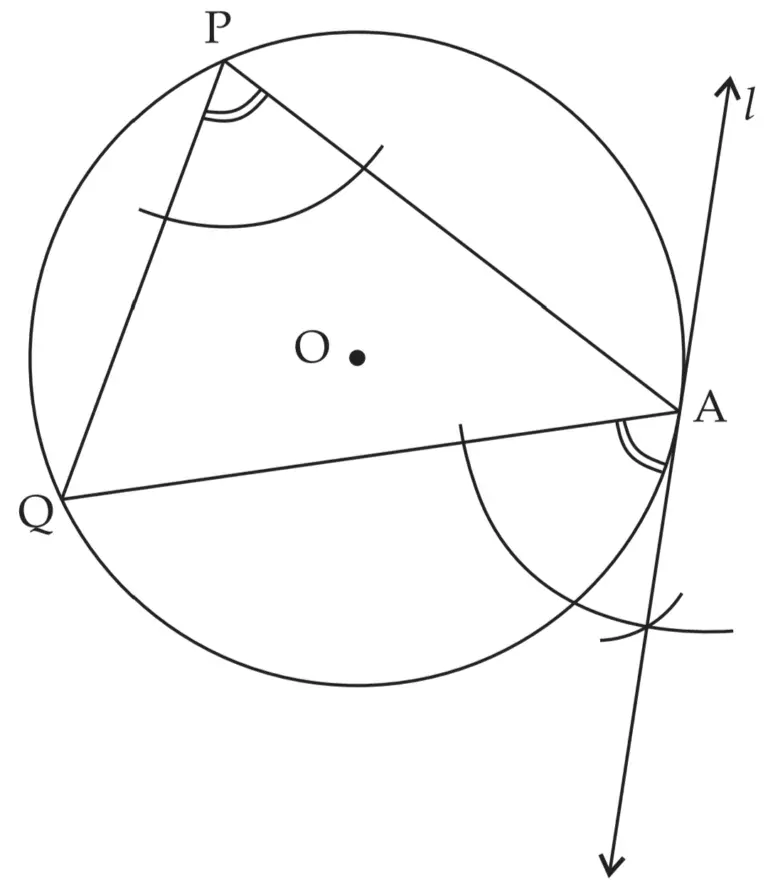
Line I is the required tangent to the circle at point A.
4. Draw a circle of diameter 6.4 cm. Take a point R at a distance equal to its diameter from the centre. Draw tangents from point R.
Solution:
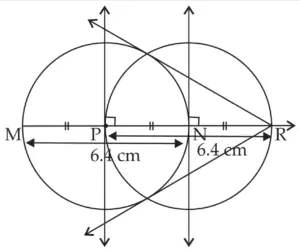
ROUGH FIGURE
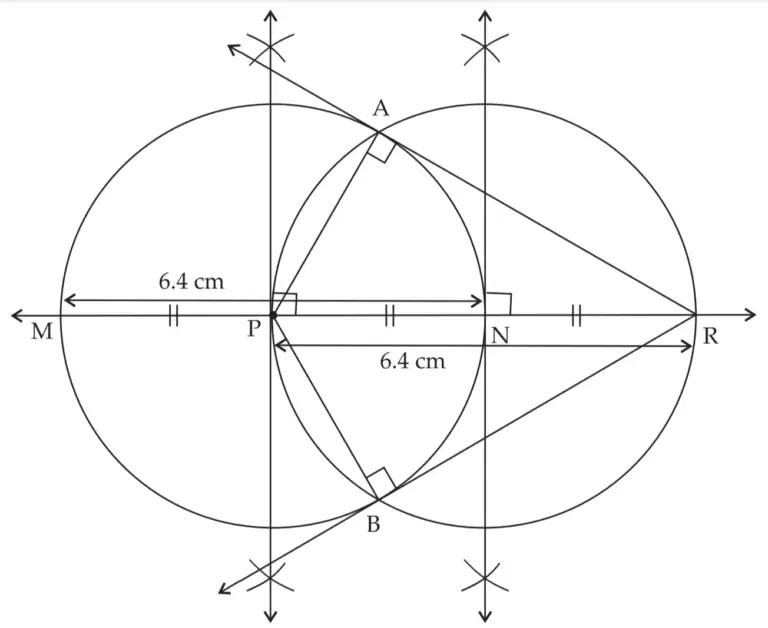
line RA and line RB are the required tangents to the circle at points A and B respectively from point R.
5. Draw a circle with centre P. Draw an arc AB of 100° measure. Draw tangents to the circle at point A and point B.
Solution:
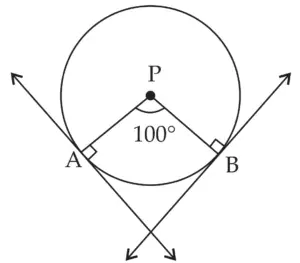
ROUGH FIGURE
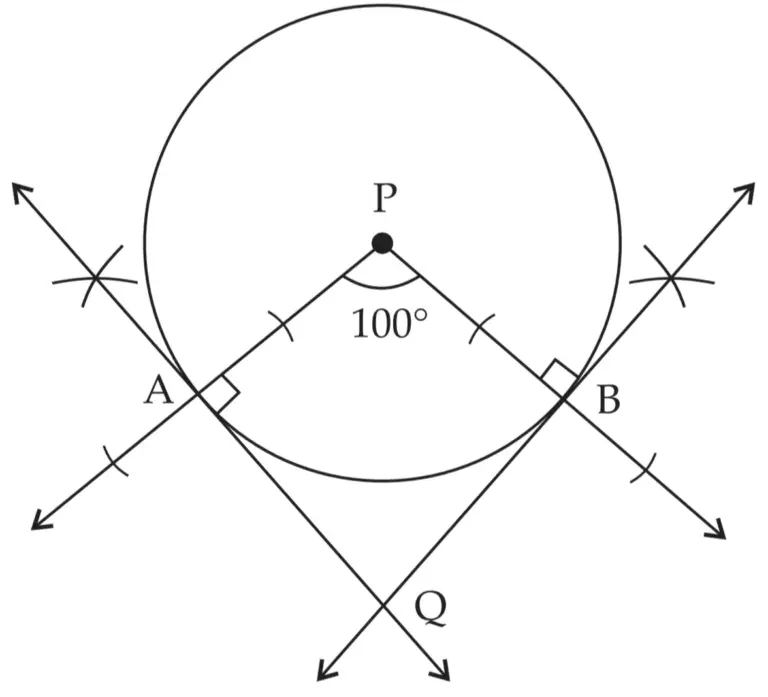
Line AQ and line BQ are tangents to the circle at points A and B respectively.
6. Draw a circle of radius 3.4 cm and centre E. Take a point F on the circle. Take another point A such that E – F – A and FA = 4.1 cm. Draw tangents to the circle from point A.
Solution:
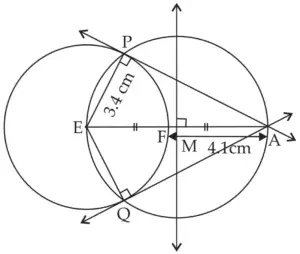
ROUGH FIGURE
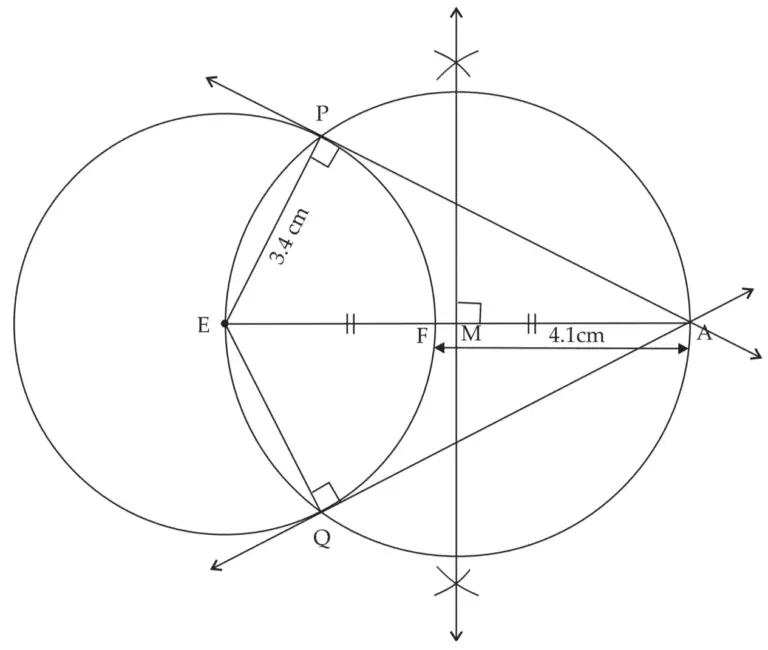
Line AP and line AQ are the required tangents from point A to the circle with centre E.
7. ∆ABC ~ ∆LBN. In ∆ABC, AB = 5.1cm, ∠B = 40°, BC=4.8 cm, \(\large \frac {AC}{LN}\) = \(\large \frac {4}{7}\). Construct ∆ABC and ∆LBN.
Solution:
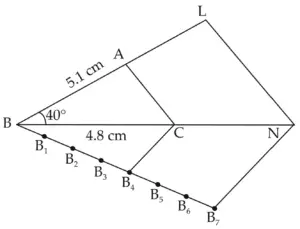
ROUGH FIGURE
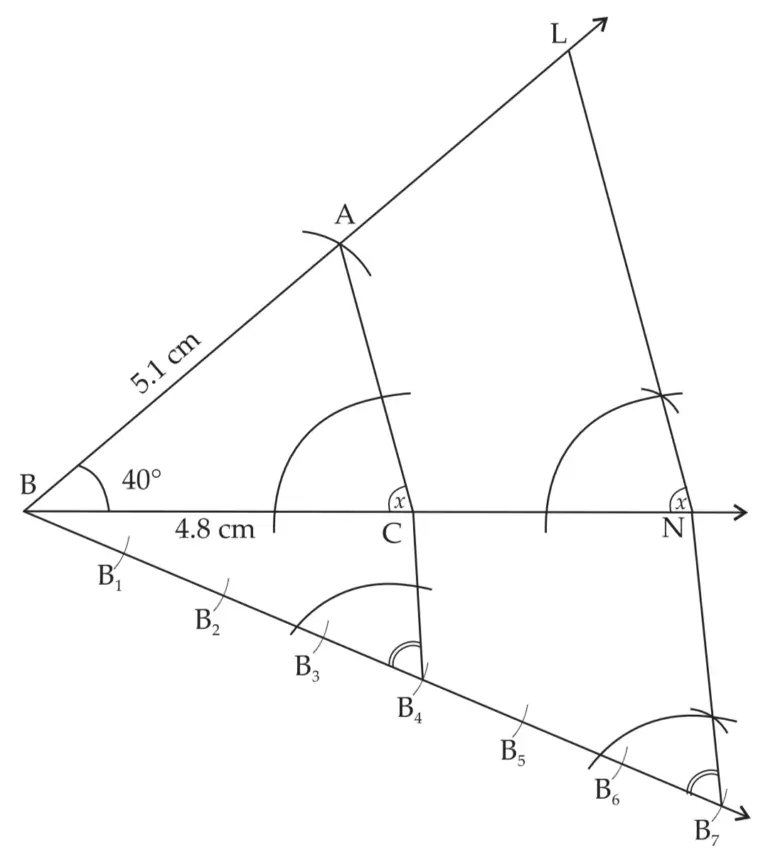
∆LBN is the required triangle similar to ∆ABC.
8. Construct ∆PYQ such that, PY = 6.3 cm, YQ = 7.2 cm, PQ = 5.8 cm. If \(\large \frac {YZ}{YQ}\) = \(\large \frac {6}{5}\), then construct ∆XYZ similar to ∆PYQ.
Solution:
ROUGH FIGURE
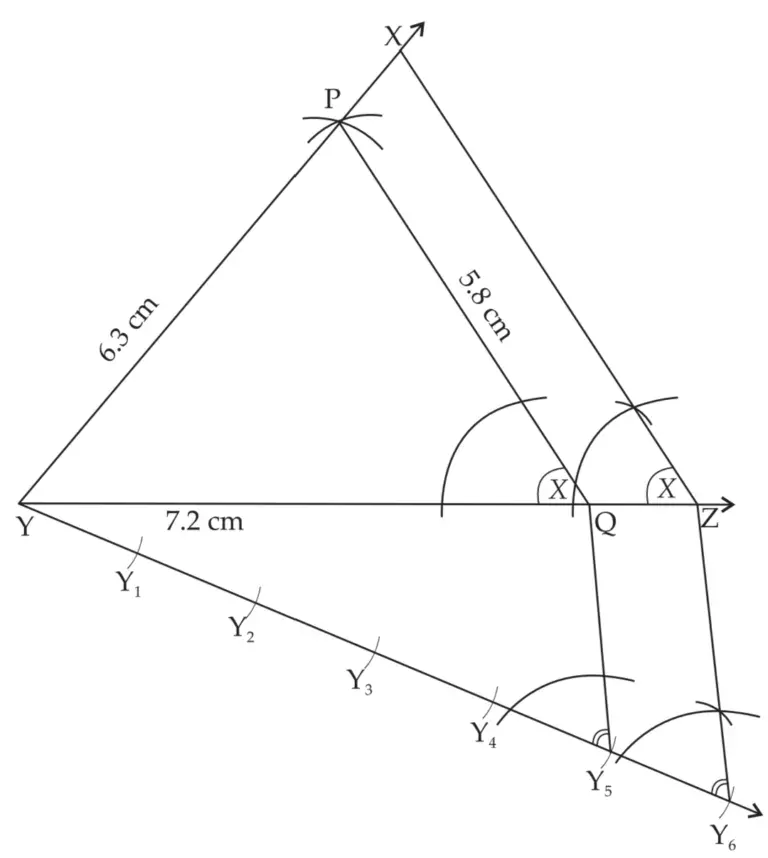
∆XYZ is the required triangle similar to ∆PYQ.
