Chapter 3 – Circle
Practice set 3.1
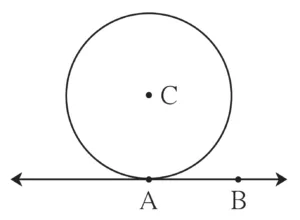
1. In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.
(1) What is the measure of ∠CAB? Why?
(2) What is the distance of point C from line AB? Why?
(3) d (A, B) = 6 cm, find d (B, C).
(4) What is the measure of ∠ABC? Why?
Given:
In a circle with centre C,
radius = 6 cm
line AB is the tangent
To find:
(1) What is the measure of ∠CAB? Why?
(2) What is the distance of point C from line AB? Why?
(3) d (A, B) = 6 cm, find d (B, C).
(4) What is the measure of ∠ABC? Why?
Solution:
(1) In circle with centre C,
radius CA ⊥ line AB …[Tangent Theorem]
∴ m∠CAB = 90º … (i)
(2) d (C, A) = 6 cm …[Radius of circle, Given]
∴ Distance of point C from line AB is 6 cm
(3) In ∆CAB,
∠CAB = 90º …[From (i)]
∴ BC² = AC² + AB² …[By Pythagoras theorem]
∴ BC² = 6² + 6²
∴ BC² = 36 + 36
∴ BC² = 72
∴ BC = 6\(\sqrt{2}\) cm …[Taking square root on both sides]
(iv) In ∆ABC,
∠A = 90º …[From (i)]
AC = AB …[Given]
∴ ∠ACB = ∠ABC … (ii) [Converse of isosceles triangle theorem]
In ∆CAB,
∠ABC + ∠ACB + ∠CAB + = 180º …[Sum of all angles of a triangle is 180º]
∴ ∠ABC +∠ABC + 90 = 180 …[From (i) and (ii)]
∴ 2∠ABC = 180 – 90
∴ 2∠ABC = 90
∴ ∠ABC = 45°
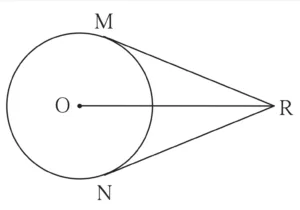
2. In the adjoining figure, O is the centre of the circle. From point R, seg RM and seg RN are tangent segments touching the circle at M and N. If (OR) = 10 cm and radius of the circle = 5 cm, then,
(1) What is the length of each tangent segment?
(2) What is the measure of ∠MRO?
(3) What is the measure of ∠MRN?
Given:
In a circle with centre O,
seg RM and seg RN are tangent segments touching the circle at M and N
OR = 10 cm
radius of the circle = 5 cm
To find:
(1) What is the length of each tangent segment?
(2) What is the measure of ∠MRO?
(3) What is the measure of ∠MRN?
Construction:
Draw seg OM and seg ON
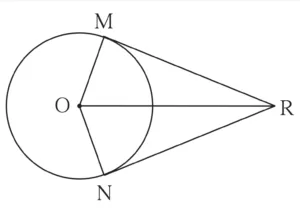
Solution:
radius OM ⊥ tangent RM …(i) [Tangent Theorem]
In ∆OMR,
∠OMR = 90⁰ …[From (i)]
∴ OR² = OM² + RM²
∴ 10² = 5² + RM²
∴ RM² = 100 – 25
∴ RM² = 75
∴ RM = 5 \(\sqrt{3}\) cm … (ii) [Taking square roots on both sides]
∴ MR = RN …[Tangent segments Theorem]
∴ RM = 5 \(\sqrt{3}\) cm …[From (ii)]
In ∆OMR,
∠OMR = 90⁰ …[From (i)]
OM = 5, OR = 10
i.e. OM = \(\large \frac {1}{2}\) OR
∴ ∠MRO = 30⁰ … (iii) [Converse of 30⁰ – 60⁰ – 90⁰]
Also,
RM = 5 \(\sqrt{3}\), OR = 10
i.e. RM = \(\large \frac {\sqrt{3}}{2}\) × OR
∴ ∠NRO = 30⁰ … (iv) [Converse of 30⁰ – 60⁰ – 90⁰]
∠MRN = ∠MRO + ∠NRO …[Angle addition property]
∴ ∠MRN = 30° + 30°
∴ ∠MRN = 60⁰
3. Seg RM and seg RN are tangent segments of a circle with centre O. Prove that seg OR bisects ∠MRN as well as ∠MON.
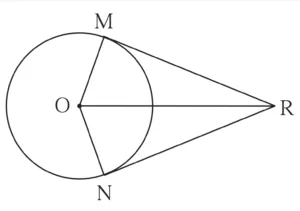
Given:
Seg RM and seg RN are tangent segments of a circle with centre O.
To prove:
seg OR bisects ∠MRN and ∠MON
Proof:
In ∆OMR and ∆ONR,
∠OMR = ∠ONR = 90° …[Tangent Theorem]
seg OR ≅ seg OR …[Common side]
seg OM ≅ seg ON …[Radii of same circle]
∴ ∆OMR ≅ ∆ONR …[By Hypotenuse – side test]
∴ ∠MOR ≅ ∠NOR … (i) [c.a.c.t.]
∴ ∠MRO ≅ ∠NRO … (ii)
∴ seg OR bisects ∠MRN and ∠MON …[From (i) and (ii)]
Hence Proved.
4. What is the distance between two parallel tangents of a circle having radius 4.5 cm? Justify your answer.
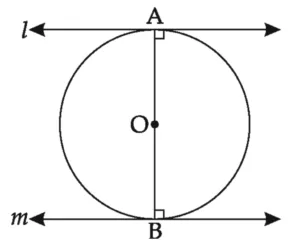
Given:
AO = OB = 4.5 cm
line l is tangent to the circle at point A
line m is tangent to the circle at point B
line l || line m
To find:
Distance between line l and line m
Solution:
seg OA ⊥ line l …(i) [Tangent Theorem]
seg OB ⊥ line m …(ii)
line l line m …(iii) [Given]
∴ A – O – B …[From (i), (ii) and (iii)]
∴ AB = AO + BO
∴ AB = 4.5 + 4.5
∴ AB = 9 cm
Ans: Distance between line l and line m is 9 cm.
Practice set 3.2
1. Two circles having radii 3.5 cm and 4.8 cm touch each other internally. Find the distance between their centres.
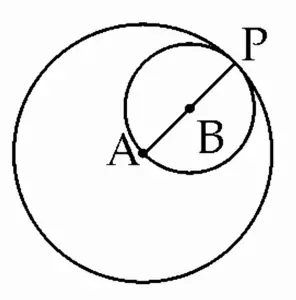
Given :
Two circles with centers A and B touch each other internally at point P.
Radius of circle with centre A is 4.8 cm.
Radius of circle with centre B is 3.5 cm.
To Find:
AB
Solution:
AP = 4.8 cm, BP = 3.5 cm …[Given]
A – B – P …[When two circles touch each other, the point of contact lies on the line joining the centres.]
∴ AP = AB + BP
∴ 4.8 = AB + 3.5
∴ AB = 4.8 – 3.5
∴ AB = 1.3 cm
∴ AB = 1.3 cm
Ans: The value of AB is 1.3 cm.
2. Two circles of radii 5.5 cm and 4.2 cm touch each other externally. Find the distance between their centres.
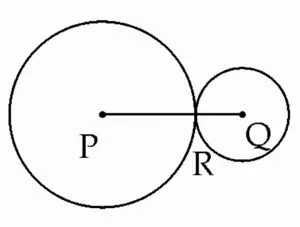
Given:
Two circles with centres P and Q touch each other externally at point R.
Radius of circle with centre P is 5.5 cm
Radius of circle with centre Q is 4.2 cm
To Find:
PQ, QR
Solution:
PR = 5.5 cm, QR = 4.2 cm …[Given]
P – R – Q …[When two circles touch each other, the point of contact lies on the line joining the two centres.]
∴ PQ = PR + QR
∴ PQ = 5.5 + 4.2
∴ PQ = 9.7 cm
∴ PQ = 9.7 cm
Ans: The value of PQ is 9.7 cm.
3. If radii of two circles are 4 cm and 2.8 cm. Draw figure of these circles touching each other –
(i) externally
(ii) internally
Solution:
Case (i): Externally touching circles.
PA = 4 cm, QA = 2.8 cm
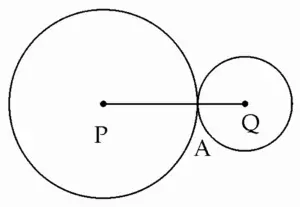
Case (ii): Internally touching circles.
PA = 4 cm, QA = 2.8 cm
4. In fig 3.27, the circles with centres P and Q touch each other at R. A line passing through R meets the circles at A and B respectively. Prove that –
(1) seg AP || seg BQ,
(2) ∆ APR ~ ∆ RQB, and
(3) Find ∠RQB if ∠PAR = 35°
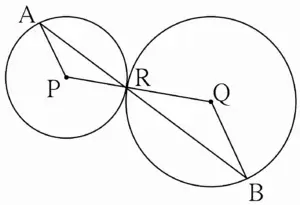
Proof and Solution:
P – R – Q …[When two circles touch each other, then point of contact lies on the line joining the two centres.]
∴ ∠PRA ≅ ∠QRB …(i) [Vertically opposite angles]
In ∆PRA,
seg PA ≅ seg PR …[Radii of same circle]
∴ ∠PRA ≅ ∠PAR …(ii) [Isosceles triangle theorem]
In ∆QRB,
seg QR ≅ seg QB …[Radii of same circle]
∴ ∠QRB ≅ ∠QBR …(iii) [Isosceles triangle theorem]
∴ ∠PRA ≅ ∠PAR ≅ ∠QRB ≅ ∠QBR …(iv) [From (i), (ii) and (iii)]
∴ ∠PAR ≅ ∠QBR …[From (iv)]
Seg AP seg BQ …[Alternate angles test]
In ∆APR and ∆RQB,
(i) ∠PAR ≅ ∠QRB …[From (iv)]
(ii) ∠PRA ≅ ∠QBR …[From (iv)]
∴ ∆APR ~ ∆RQB …[By AA test of similarity]
∴ ∠PAR = 35⁰ …(v) [Given]
∴ ∠QRB = ∠QBR = 35⁰ …(vi) [From (iv) and (v)]
In ∆QRB
∠RQB + ∠QRB + ∠QBR = 180⁰ …[Sum of all angles of a ∆ is 180⁰]
∴ ∠RQB + 35⁰ + 35⁰ = 180⁰ …[From (vi)]
∴ ∠RQB = 180⁰ – 70⁰
∴ ∠RQB = 110⁰
Ans: The value of ∠RQB is 110⁰
5. In fig 3.28 the circles with centres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD if the radii of the circles are 4 cm, 6 cm.
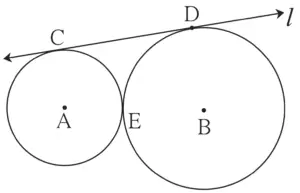
Construction:
Draw seg AC and seg BD
Draw seg AF ⊥ seg BD, B – F – D.
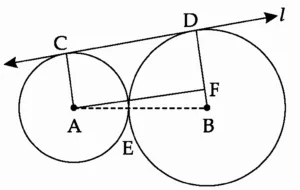
Solution:
A – E – B … (i) [When two circles touch each other, the point of contact lies on the line joining the centres.]
∴ AC = AE = 4 cm …(ii) [Given, radii of same circle]
∴ BD = BE = 6 cm …(iii) [Given, radii of same circle]
AB = AE + BE …[A – E – B, from (i)]
∴ AB = 4 + 6 …[From (ii) and (iii)]
∴ AB = 10 cm …(iv)
In □ ACDF,
∠ACD = 90⁰ [Tangent and radius are ⊥ to each other at the point of contact]
∠FDC = 90⁰
∠AFD = 90⁰ …[Construction]
∠FAC = 90⁰ …[Remaining angle]
∴ □ ACDF is a rectangle …[Definition]
∴ CD = AF …(v) [Opposite sides of rectangle are equal]
FD = AC …(vi) [Opposite sides of rectangle are equal]
∴ FD = 4 cm …(vii) …[From (ii) and (vi)]
BD = BF + FD …[B – F – D]
∴ 6 = BF + 4 …[From (iii) and (vii)]
∴ BF = 6 – 4 = 2 cm …(viii)
In ∆AFB,
∠AFB = 90 …[Construction]
∴ AB = AF² + BF² …[By Pythagoras theorem]
∴ 10² = AF² + 2²
∴ AF² = 100 – 4
∴ AF² = 96
∴ AF = \(\sqrt{97}\) …[Taking square roots]
∴ AF = \(\sqrt{16\,×\,6}\)
∴ AF = 4 \(\sqrt{6}\) cm
∴ CD = 4 \(\sqrt{6}\) cm …[From (v)]
Practice set 3.3
1. In figure 3.37, points G, D, E, F are concyclic points of a circle with centre C. ∠ECF = 70°, m(arc DGF) = 200° find m(arc DE) and m(arc DEF).
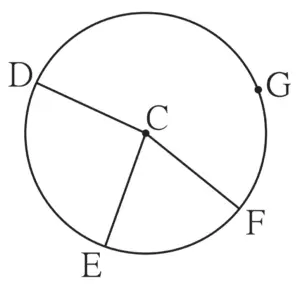
Given :
Points G, D, E, F are concyclic points
∠ECF = 70°
m(arc DGF) = 200°
To find:
m(arc DE) and m(arc DEF)
Solution:
m(arc EF) = m∠ECF …[Definition of measure of a minor arc]
∴ m(arc EF) = 70⁰ …(i)
m(arc DE) + m(arc EF) + m(arc DGF) = 360⁰ …[Measure of a circle is 360⁰]
∴ m(arc DE) + 70⁰ + 200⁰ = 360⁰ …[From (i) and given]
∴ m(arc DE) = 360⁰ – 270⁰
∴ m(arc DE) = 90⁰
m(arc DEF) + m(arc DE) + m(arc EF) …[Arc addition property]
∴ m(arc DEF) = 90⁰ + 70⁰ …[From (i) and given]
∴ m(arc DEF) = 160⁰
2. In fig 3.38 ∆QRS is an equilateral triangle. Prove that,
(1) arc RS ≅ arc QS ≅ arc QR
(2) m(arc QRS) = 240°
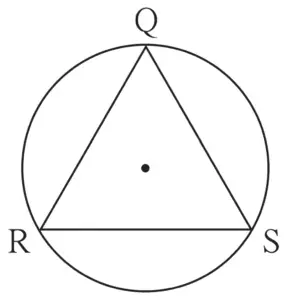
Given:
∆QRS is an equilateral triangle
To prove:
(1) arc RS ≅ arc QS ≅ arc QR
(2) m(arc QRS) = 240°
Proof:
(1) ∆QRS is an equilateral triangle …[Given]
∴ chord QR ≅ chord RS ≅ chord QS …[Sides of equilateral triangle are equal]
arc RS ≅ arc QS ≅ arc QR …(i) [In circle, congruent chords have corresponding minor arcs are congruent]
Hence proved.
(2) Let m (arc RS) = m (arc QS) = m (arc QR) = x …(ii) [From (i) and supposition]
∴ m (arc RS) + m (arc QS) + m (arc QR) = 360⁰ …[Measure of a circle is 360⁰]
∴ x + x + x = 360⁰
∴ 3x = 360⁰
∴ x = \(\large \frac {360}{3}\)
∴ x = 120⁰
∴ m (arc RS) = m (arc QS) + m (arc QR) = 120⁰ …(iii)
∴ m (arc QRS) = m (arc QR) + m (arc RS) …[Arc addition property]
∴ m (arc QRS) = 120⁰ + 120⁰ …[From (iii)]
∴ m(arc QRS) = 240⁰
Hence proved.
3. In fig 3.39 chord AB ≅ chord CD, Prove that, arc AC ≅ arc BD
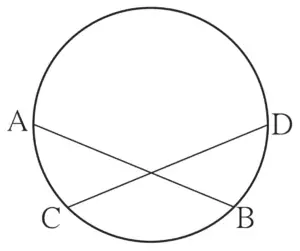
Given:
chord AB ≅ chord CD
To prove:
arc AC ≅ arc BD
Proof:
chord AB ≅ chord CD …[Given]
∴ arc ACB ≅ arc DBC …[In a circle, congruent chords have their corresponding minor arcs are congruent]
m (arc ACB) = m (arc DBC)
∴ m (arc AC) + m (arc CB) = m (arc CB) + m (arc BD) …[Arc addition property]
∴ m (arc AC) = m (arc BD)
∴ arc AC ≅ arc BD
Hence proved.
Practice set 3.4
1. In figure 3.56, in a circle with centre O, length of chord AB is equal to the radius of the circle. Find measure of each of the following.
(1) ∠AOB
(2) ∠ACB
(3) arc AB
(4) arc ACB
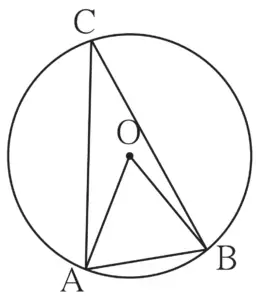
Given :
OA and OB are the radii of the circle
AB = OA = OB
To find:
(1) ∠AOB
(2) ∠ACB
(3) arc AB
(4) arc ACB
Solution:
AB = OA = OB …[Given]
∴ ∆OAB is an equilateral triangle …[By definition]
∴ ∠AOB = 60⁰ …[Measure of an angle of an equilateral triangle]
∴ m (arc AB) = m∠AOB …[Definition of measure of minor arc]
∴ m(arc AB) = 60°
∠ACB = \(\large \frac {1}{2}\) (arc AB) …[Inscribed angle theorem]
∴ ∠ACB = \(\large \frac {1}{2}\) × 60
∴ ∠ACB = 30°
m (arc ACB) + m (arc AB) = 360° …[Measure of a circle is 360°]
∴ m (arc ACB) + 60° = 360°
∴ m (arc ACB) = 360° – 60°
∴ m(arc ACB) = 300°
2. In figure 3.57, □ PQRS is cyclic. side PQ ≅ side RQ. ∠PSR = 110°, Find
(1) measure of ∠PQR
(2) m(arc PQR)
(3) m(arc QR)
(4) measure of ∠PRQ
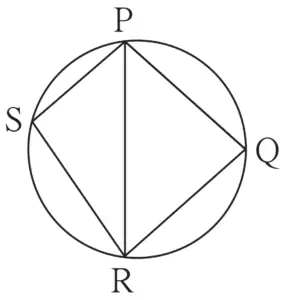
Given:
□ PQRS is cyclic
side PQ ≅ side RQ
∠PSR = 110°
To find:
(1) measure of ∠PQR
(2) m(arc PQR)
(3) m(arc QR)
(4) measure of ∠PRQ
Solution:
□PQRS is a cyclic quadrilateral …[Given]
∴ ∠PQR + ∠PSR = 180° …[Cyclic quadrilateral theorem]
∴ ∠PQR + 110° = 180°
∴ ∠PQR = 180° – 110°
∴ m∠PQR = 70° …(i)
∠PSR = \(\large \frac {1}{2}\) m(arc PQR) …[Inscribed angle theorem]
∴ 110° = \(\large \frac {1}{2}\) × m(arc PQR) … (v) [From (iv)]
∴ m(arc PQR) = 220° …(ii)
In ∆PQR,
side PQ ≅ side RQ …[Given]
∴ ∠QPR ≅ ∠QRP …(iii) [Isosceles triangle theorem]
In ∆PQR,
∠PQR + ∠PRQ + ∠QPR = 180°…[Sum of all angles of a triangle is 180°]
∴ 70° + ∠QPR + ∠QPR = 180° …[From (i) and (ii)]
∴ 2 ∠QPR = 180° – 70°
∴ 2 ∠QPR = 110°
∴ ∠QPR = 55° …(iv)
∴ ∠QRP = 55° …[From (iii) and (iv)]
∠QPR = \(\large \frac {1}{2}\) × m(arc QR) …[Inscribed angle theorem]
∴ 55 = \(\large \frac {1}{2}\) × m(arc QR) …[From (iv)]
∴ m(arc QR) = 110° …[From (iii) and (iv)]
3. □ MRPN is cyclic, ∠R = (5x – 13)°, ∠N = (4x + 4)°. Find measures of ∠R and ∠N.
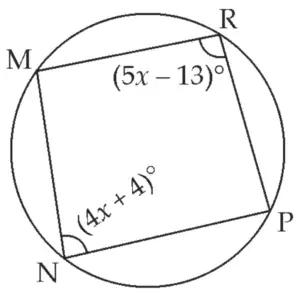
Given:
□ MRPN is cyclic
∠R = (5x – 13)°
∠N = (4x + 4)°.
To find:
∠R and ∠N
Solution:
□ MRPN is a cyclic quadrilateral …[Given]
∴ ∠R + ∠N = 180° …[Cyclic quadrilateral theorem]
∴ 5x – 13 + 4x + 4 = 180
∴ 9x – 9 = 180
∴ 9x = 180 + 9
∴ 9x = 189
∴ x = \(\large \frac {189}{9}\)
∴ x = 21
m∠R = 5x – 13
∴ m∠R = 5 × 21 – 13
∴ m∠R = 105 – 13
∴ m∠R = 92°
& = 4x + 4
∴ m∠N = 4 × 21 + 4
∴ m∠N = 84 + 4
∴ m∠N = 88°
4. In figure 3.58, seg RS is a diameter of the circle with centre O. Point T lies in the exterior of the circle. Prove that ∠ RTS is an acute angle.
Given:
Seg RS is the diameter
Point T lies in the exterior of the circle
To Prove:
∠RTS is an acute angle
Construction:
Draw seg PS
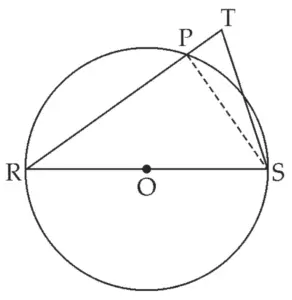
Proof:
seg RS is the diameter of the circle. …[Given]
∴ ∠RPS = 90° …(i) [Diameter subtends a right angle at any point of the circle]
∠RPS is an exterior angle of ∠PTS …[Definition]
∴ ∠RPS > ∠PTS …[Exterior angle theorem]
i.e. ∠PTS < ∠RPS
∴ ∠PTS < 90° …[From (i)]
i.e. ∠RTS < 90° …[R – P – T]
∴ ∠RTS is an acute angle.
Hence proved.
5. Prove that any rectangle is a cyclic quadrilateral.

Given:
□PQRS is a rectangle
To Prove:
□PQRS is a cyclic quadrilateral
Proof:
□ PQRS is a rectangle …[Given]
∴ ∠P = ∠Q = ∠R = ∠S = 90° …(i) [Angles of rectangle]
∠P + ∠R = 90° + 90° …[From (i)]
∴ ∠P + ∠R = 180°
i.e. opposite angles of □PQRS are supplementary
∴ □ PQRS is cyclic quadrilateral …[Converse of cyclic quadrilateral theorem]
Hence proved.
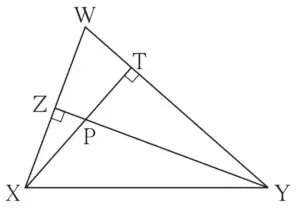
6. In figure 3.59, altitudes YZ and XT of ∆WXY intersect at P. Prove that,
(1) □ WZPT is cyclic.
(2) Points X, Z, T, Y are concyclic.
Given:
Altitudes YZ and XT of ∆WXY intersect at P.
To Prove:
(i) □ WZPT is a cyclic quadrilateral
(ii) Points X, Z, T and Y are concyclic points.
Proof:
∠XTW = 90° …(i) [Given]
∠YZW = 90° …(ii) [Given]
∴ ∠XTW + ∠YZW = 90° + 90°…[Adding (i) and (ii)]
∴ ∠PTW + ∠PZW = 180° …[X – P – T, Y – P – Z]
□ WZPT is a cyclic quadrilateral …[Converse of cyclic quadrilateral theorem]
Hence proved.
∠XZY = ∠XTY = 90° …[Given]
∴ ∠XZY = ∠XTY
∴ seg XY subtends congruent angle at points Z and T which are on the same side of line XY.
∴ Point X, Z, T and Y are concyclic points.
Hence proved.
7. In figure 3.60, m(arc NS) = 125°, m(arc EF) = 37°, find the measure ∠NMS.
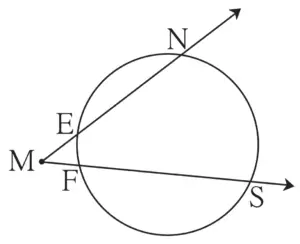
Given:
m(arc NS) = 125°
m(arc EF) = 37°
To find:
∠NMS
Solution:
m∠NMS = \(\large \frac {1}{2}\) [m(arc NS) – m(arc EF)]
∴ m∠NMS = \(\large \frac {1}{2}\) × (125° – 37°)
∴ m∠NMS = \(\large \frac {1}{2}\) × 88
∴ m∠NMS = 44°
8. In figure 3.61, chords AC and DE intersect at B. If ∠ ABE = 108°, m(arc AE) = 95°, find m(arc DC).
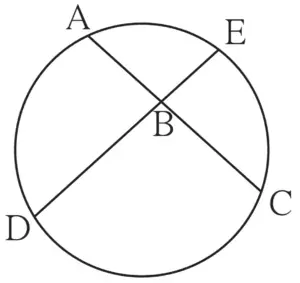
Given:
Chords AC and DE intersect at B
∠ABE = 108°
m(arc AE) = 95°
To find:
m(arc DC)
Solution:
m∠ABE = \(\large \frac {1}{2}\) [m(arc DC) + m(arc AE)]
∴ 108 = \(\large \frac {1}{2}\) [m(arc DC) + 95°]
∴ 108 × 2 = m(arc DC) + 95°
∴ 216 = m(arc DC) + 95°
∴ m(arc DC) = 216 – 95°
∴ m(arc DC) = 121°
Practice set 3.5
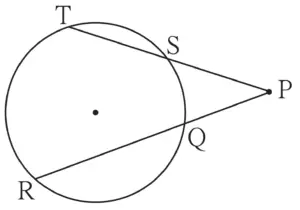
1. In figure 3.77, ray PQ touches the circle at point Q. PQ = 12, PR = 8, find PS and RS.
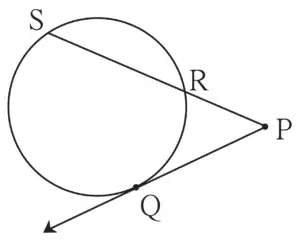
Given:
Ray PQ touches the circle at point Q
PQ = 12
PR = 8
To find:
PS and RS
Solution:
Tangent PQ and secant PRS intersect each other at point P.
∴ PQ² = PR × PS …[Tangent secant segments theorem]
∴ 12² = 8 × PS
∴ \(\large \frac {144}{8}\) = PS
∴ PS = 18 units
PS = PR + RS …[P – R – S]
∴ 18 = 8 + RS
∴ RS = 18 – 8
∴ RS = 10 units
2. In figure 3.78, chord MN and chord RS intersect at point D.
(1) If RD = 15, DS = 4, MD = 8 find DN
(2) If RS = 18, MD = 9, DN = 8 find DS
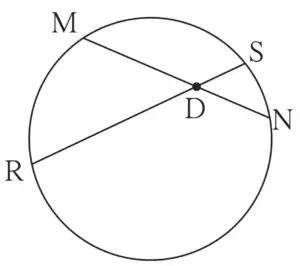
Given:
Chord MN and chord RS intersect at point D
RD = 15
DS = 4
MD = 8
RS = 18
MD = 9
DN = 8
Solution:
(1) Chord MN and Chord RS intersect each other in the interior of the circle at point D.
∴ DM × DN = DR × DS …[Theorem of internal division of chords]
∴ 8 × DN = 15 × 4
∴ 8 × DN = 60
∴ DN = \(\large \frac {60}{8}\)
∴ DN = 7.5 units
(2) Let DS = x …(i) [Supposition]
RS = DR + DS …[R – D – S]
∴ 18 = DR + x
∴ DR = (18 – x) …(ii)
Chord MN and Chord RS intersect each other in the interior of the circle at point D.
∴ DM × DN = DR × DS …[Theorem of internal division of chords]
∴ 9 × 8 = x (18 – x)
∴ 72 = 18x – x2
∴ x² – 18x + 72 = 0
∴ x² – 12x – 6x + 72 = 0
∴ x(x – 12) – 6(x – 12) = 0
∴ (x – 12) (x – 6) = 0
∴ x – 12 = 0 or x – 6 = 0
∴ x = 12 or x = 6
∴ DS = 12 units or DS = 6 units
3. In figure 3.79, O is the centre of the circle and B is a point of contact. seg OE ⊥ seg AD, AB = 12, AC = 8, find
(1) AD
(2) DC
(3) DE
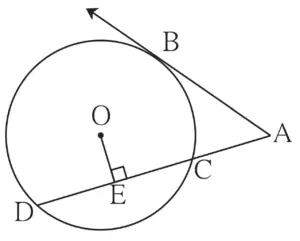
Given:
seg OE ⊥ seg AD
AB = 12
AC = 8
To find:
(1) AD
(2) DC
(3) DE
Solution:
Tangent AB and Secant ACD intersect at point A.
∴ AB² = AC × AD …[Tangent secant segments theorem]
∴ 12² = 8 × AD
∴ 144 = 8 × AD
∴ \(\large \frac {144}{8}\) = AD
∴ AD = 18 units
AD = AC + DC ..[A – C – D]
∴ 18 = 8 + DC
∴ DC = 18 – 8
∴ DC = 10 units
Seg DE ⊥ chord CD …[Given]
∴ OE = \(\large \frac {1}{2}\) + CD …[Perpendicular drawn from the centre of the circle to the chord bisects the chord]
∴ DE = \(\large \frac {1}{2}\) × 10 …[From (i)]
∴ DE = 5 units
4. In figure 3.80, if PQ = 6, QR = 10, PS = 8 find TS.
Given:
PQ = 6
QR = 10
PS = 8
To Prove:
TS
Solution:
PR = PQ + QR …[P – Q – R]
∴ PR = 6 + 10
∴ PR = 16 units …(i)
Secants PST and PQR intersect each other in the exterior of the circle at point P.
∴ PT × PS = PR × PQ …[Theorem of external division of chords]
∴ PT × 8 = 16 × 6 …[From (i) and given]
∴ PT × 8 = 96
∴ PT = \(\large \frac {96}{8}\)
∴ PT = 12 units …(ii)
∴ PT = PS + TS …[P – S – T]
∴ 12 = 8 + TS
∴ TS = 12 – 8
∴ TS = 4 units
5. In figure 3.81, seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE × GE = 4r²
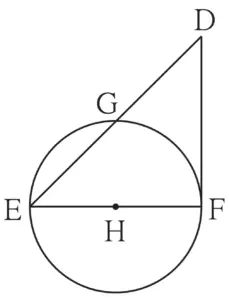
Given:
Seg EF is a diameter
Seg DF is a tangent segment
Radius of the circle is r
To prove:
DE × GE – 4r²
Construction:
Draw seg GF
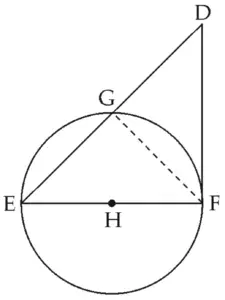
Proof:
∠EGF = 90° …(i) [Diameter subtends a right angle at any point on the circle]
In ∆EFD,
∠EFD = 90° …[Tangent and radius are perpendicular at the point of contact]
seg FG ⊥ hypotenuse ED …[From (i)]
∴ ∆EFD ~ ∆EGF ~ ∆FGD …(ii) [Similarity in right angled triangles]
∴ ∆EFD ~ ∆EGF …[From (ii)]
∴ \(\large \frac {EF}{GE}\) = \(\large \frac {DE}{EF}\) …[c.s.c.t.]
∴ DE × GE = EF²
∴ DE × GE = (2r)² …[Diameter is twice the radius]
∴ DE × GE = 4r²
Hence proved.
Problem set 3
1. Four alternative answers for each of the following questions are given. Choose the correct alternative.
(1) Two circles of radii 5.5 cm and 3.3 cm respectively touch each other. What is the distance between their centers?
(A) 4.4 cm
(B) 8.8 cm
(C) 2.2 cm
(D) 8.8 or 2.2 cm
Ans: Option (D) : 8.8 or 2.2 cm
Solution:
The radii of the two circles are 5.5 cm and 3.3 cm.
Case 1: If two circles touch each other externally, distance between their centres is equal to the sum of their radii.
Distance between their centres
= 5.5 cm + 3.3 cm
= 8.8 cm
Case 2: If two circles touch each other internally, distance between their centres is equal to the difference of their radii.
Distance between their centres
= 5.5 cm – 3.3 cm
= 2.2 cm
Thus, the distance between their centres is 8.8 cm or 2.2 cm
(2) Two circles intersect each other such that each circle passes through the centre of the other. If the distance between their centres is 12, what is the radius of each circle?
(A) 6 cm
(B) 12 cm
(C) 24 cm
(D) can’t say
Ans: Option (B) : 12 cm
Solution:
Two circles intersect each other such that each circle passes through the center of the other. This can happen only when the two circles are of the same radius.
Hence, the distance between their centers is equal to the radius of each circle.
Therefore, the radius of both circle is 12.
(3) A circle touches all sides of a parallelogram. So the parallelogram must be a ______.
(A) rectangle
(B) rhombus
(C) square
(D) trapezium
Ans: Option (B) : rhombus
Solution:
Let ABCD be a parallelogram whose sides AB, BC, CD and DA touch a circle at the points P, Q, R and S respectively.
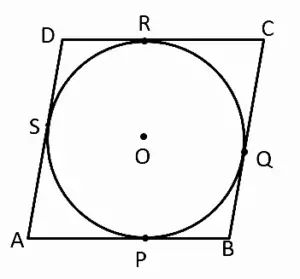
Since, the lengths of tangents drawn from an external point to a circle are equal, we have;
AP = AS, BP = BQ, CR = CQ and DR = DS.
AB + CD
= AP + BP + CR + DR
= AS + BQ + CQ + DS
= (AS + DS) + (BQ+CQ)
= AD + BC
Now,
AB + CD = AD + BC
∴ 2AB = 2BC
∴ AB = BC
∴ AB = BC = CD = AD
Hence, ABCD is a rhombus.
(4) Length of a tangent segment drawn from a point which is at a distance 12.5 cm from the centre of a circle is 12 cm, find the diameter of the circle.
(A) 25 cm
(B) 24 cm
(C) 7 cm
(D) 14 cm
Ans: Option (C) : 7 cm
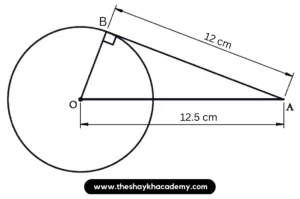
(5) If two circles are touching externally, how many common tangents of them can be drawn?
(A) One
(B) Two
(C) Three
(D) Four
Ans: Option (C) – Three
(6) ∠ACB is inscribed in arc ACB of a circle with centre O. If ∠ACB = 65°, find m(arc ACB).
(A) 65°
(B) 130°
(C) 295°
(D) 230°
Ans: Option (D) : 230°
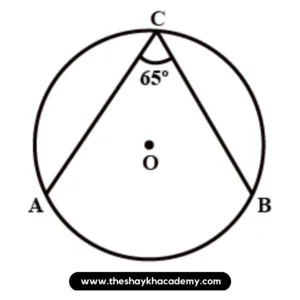
Solution:
The measure of an inscribed angle is half of the measure of the arc intercepted by it.
m∠ACB = \(\large \frac {1}{2}\) m(arc AB) …[Inscribed angle theorem]
∴ m(arc AB) = 2 m∠ACB
∴ m(arc AB) = 2 × 65°
∴ m(arc AB) = 130⁰
m(arc ACB) = 360° – m(arc AB) …[Measure of a circle is 360°]
∴ m(arc ACB) = 360⁰ – 130⁰
∴ m(arc ACB) = 230⁰
(7) Chords AB and CD of a circle intersect inside the circle at point E. If AE = 5.6, EB = 10, CE = 8, find ED.
(A) 7
(B) 8
(C) 11.2
(D) 9
Ans: Option (A) : 7
Solution:
AE × EB = CE × ED
∴ 5.6 × 10 = 8 × ED
∴ 56 = 8 × ED
∴ ED = \(\large \frac {56}{8}\)
∴ ED = 7
(8) In a cyclic □ABCD, twice the measure of ∠A is thrice the measure of ∠C. Find the measure of ∠C?
(A) 36
(B) 72
(C) 90
(D) 108
Ans: Option (B) : 72⁰
Solution:
ABCD is a cyclic quadrilateral.
2∠A = 3∠C …[Given]
∴ ∠A = \(\large \frac {3}{2}\)∠C …(i)
Now,
∠A + ∠C = 180° …[Opposite angles of a cyclic quadrilateral are supplementary]
∴ \(\large \frac {3}{2}\) ∠C + ∠C = 180° …[From (i)]
∴ \(\large \frac {5}{2}\) ∠C = 180°
∴ ∠C = \(\large \frac {2}{5}\) × 180°
∴ ∠C = 72°
(9) Points A, B, C are on a circle, such that m(arc AB) = m(arc BC) = 120°. No point, except point B, is common to the arcs. Which is the type of ∆ABC?
(A) Equilateral triangle
(B) Scalene triangle
(C) Right angled triangle
(D) Isosceles triangle
Ans: Option (A) : Equilateral triangle
Solution:
m(arc AB) = m(arc BC) = 120°
Now,
m(arc AB) + m(arc BC) + m(arc CA) = 360°
∴ 120° + 120° + m(arc CA) = 360°
∴ 240° + m(arc CA) = 360°
∴ m(arc CA) = 360° – 240°
∴ m(arc CA) = 120°
∴ m(arc AB) = m(arc BC) = m(arc CA)
∴ arc AB = arc BC arc CA …[Two arcs are congruent if their measures are equal]
∴ chord AB = chord BC = chord CA …[Chords corresponding to congruent arcs of a circle are congruent]
∴ ∆ABC is an equilateral triangle. ..[All sides of equilateral triangle are equal]
(9) Points A, B, C are on a circle, such that m(arc AB) = m(arc BC) = 120°. No point, except point B, is common to the arcs. Which is the type of ∆ABC?
(A) Equilateral triangle
(B) Scalene triangle
(C) Right angled triangle
(D) Isosceles triangle
Ans: Option (A) : Equilateral triangle
Solution:
Let P be any point on the arc XZ.
m(arc AB) = m(arc BC) = 120°
Now,
m(arc AB) + m(arc BC) + m(arc CA) = 360°
∴ 120° + 120° + m(arc CA) = 360°
∴ 240° + m(arc CA) = 360°
∴ m(arc CA) = 360° – 240°
∴ m(arc CA) = 120°
∴ m(arc AB) = m(arc BC) = m(arc CA)
∴ arc AB = arc BC arc CA …[Two arcs are congruent if their measures are equal]
∴ chord AB = chord BC = chord CA …[Chords corresponding to congruent arcs of a circle are congruent]
∴ ∆ABC is an equilateral triangle …[All sides of equilateral triangle are equal]
(10) Seg XZ is a diameter of a circle. Point Y lies in its interior. How many of the following statements are true?
(i) It is not possible that ∠XYZ is an acute angle.
(ii) ∠XYZ can’t be a right angle.
(iii) ∠XYZ is an obtuse angle.
(iv) Can’t make a definite statement for measure of ∠XYZ.
(A) Only one
(B) Only two
(C) Only three
(D) All
Ans: Option (C) : Only three
Solution:
XZ is the diameter of the circle.
∴ XPZ = 90° …[Angle in a semicircle is 90°]
∴ XYZ cannot be a right angle.
In ∆YPZ,
∠XYZ > ∠YPZ …[An exterior angle of a triangle is greater than its remote interior angle]
∴ ∠XYZ > 90° …[∠YPZ ≅ ∠XPZ]
So, XYZ is an obtuse angle.
Therefore, it is not possible that XYZ is an acute angle. Thus, three of the following statements are true.
2. Line l touches a circle with centre O at point P. If radius of the circle is 9 cm, answer the following.
(1) What is d(O, P) = ? Why ?
(2) If d(O, Q) = 8 cm, where does the point Q lie ?
(3) If d(O, R)* = 15 cm, How many locations of point R are line on line l ? At what distance will each of them be from point P? (*correction in textbook)
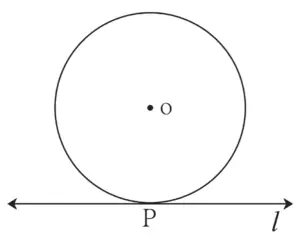
Given:
Radius of the circle = 9 cm
d(O, Q) = 8 cm
d(O, R) = 15 cm
Solution:
(i) Radius of the circle is 9 cm.
∴ d(O, P) = 9 cm
(ii) d(O, Q) = 8 cm
d(Q, O) < Radius
∴ Point Q lies in the interior of the circle.
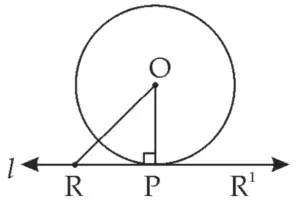
(iii) Point can have two different positions on line l as shown in the adjoining figure.
In ∆OPR,
∠OPR = 90 ° …[Tangent Theorem]
∴ OR² = OP² + PR² …[Pythagoras theorem]
∴ 15² = 9² + PR²
∴ PR² = 225 – 81
∴ PR² = 144
∴ PR² = 144
∴ PR = 12 units …[Taking square roots]
Ans: Two such ‘R’ are contained in line l.
3. In figure 3.83, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL = 6 3 then find –
(1) Radius of the circle.
(2) Measures of ∠K and ∠M.
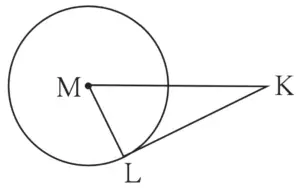
Given:
M is the centre of the circle
Seg KL is a tangent segment
MK = 12
KL = 6\(\sqrt{3}\)
Solution:
(i) In ∆MLK,
∠MLK = 90⁰ …(i) [Tangent and radius are perpendicular at the point of contact]
∴ MK² = ML² + LK² …[Pythagoras theorem]
∴ 12² = ML² + (6\(\sqrt{3}\))²
∴ 144 = ML² + 108
∴ ML² = 144 –108
∴ ML² = 36
∴ ML = 6 units …(ii) [Taking square roots]
∴ Radius of the circle is 6 units.
(ii) In ∆MLK,
∠MLK = 90⁰ …[From (i)]
ML = \(\large \frac {1}{2}\) × MK …[From (ii) and given]
∴ ∠K = 30⁰ …[Converse of 30⁰ – 60⁰ – 90⁰ theorem]
∴ ∠M = 60⁰ …[∵ Sum of all angles of a triangle is 180⁰]
4. In figure 3.84, O is the centre of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB) = r, Prove that, □ ABOC is a square.
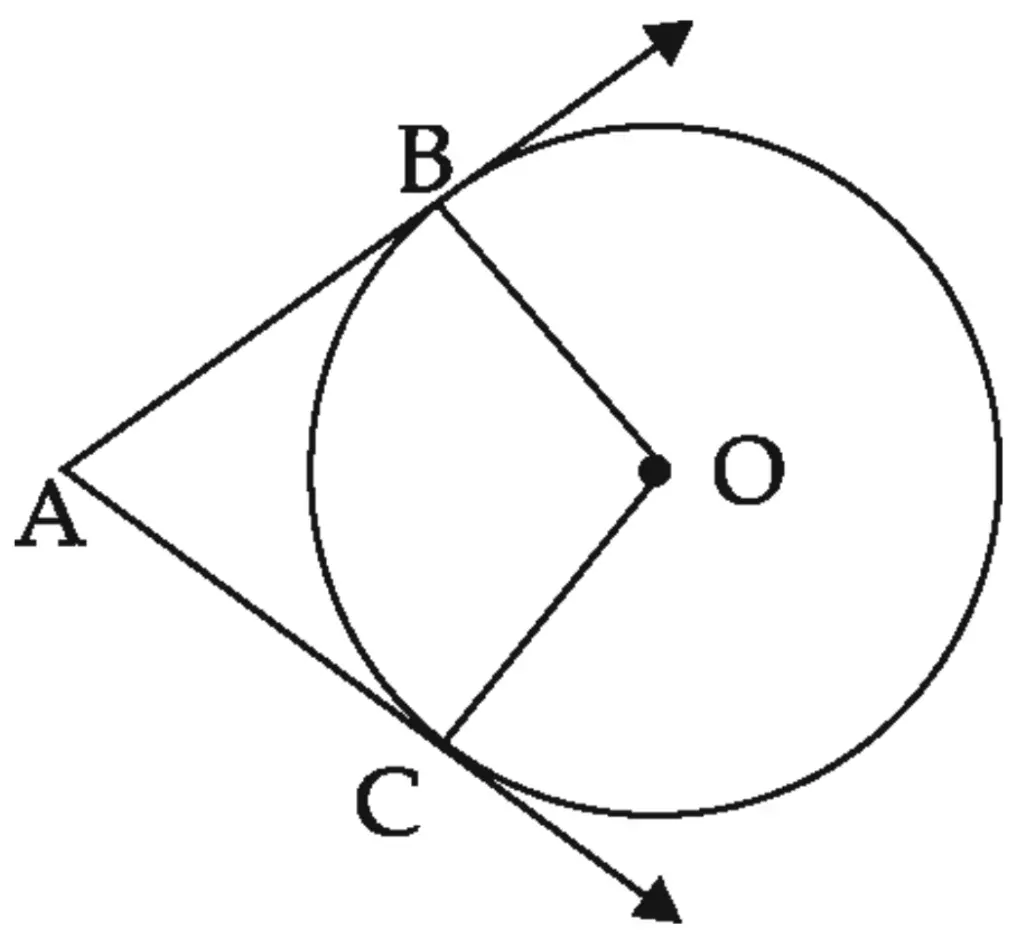
Given:
O is the centre of the circle
Seg AB, seg AC are tangent segments
Radius of the circle is r
l(AB) = r
To prove:
□ ABOC is a square
Proof:
seg AB ≅ seg AC …(i) [Tangent segment Theorem]
l(AB) = r …(ii) …[Given]
l(AB) = l(AC) = r …(iii) [From (i) and (ii)]
l(OB) = l(OC) = r …(iv) [Radii of the same circle]
In ∆BOC,
seg AB ≅ seg AC ≅ seg OB ≅ seg OC …[From (iii) and (iv)]
∴ ∆BOC is a rhombus …(v) [Definition]
But, ∠OBA = 90⁰ …(vi) [Tangent Theorem]
In rhombus ABOC,
∠OBA = 90⁰ …[From (v) and (vi)]
∴ □ ABOC is a square …[Definition]
Hence proved.
5. In figure 3.85, □ ABCD is a parallelogram. It circumscribes the circle with center T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.
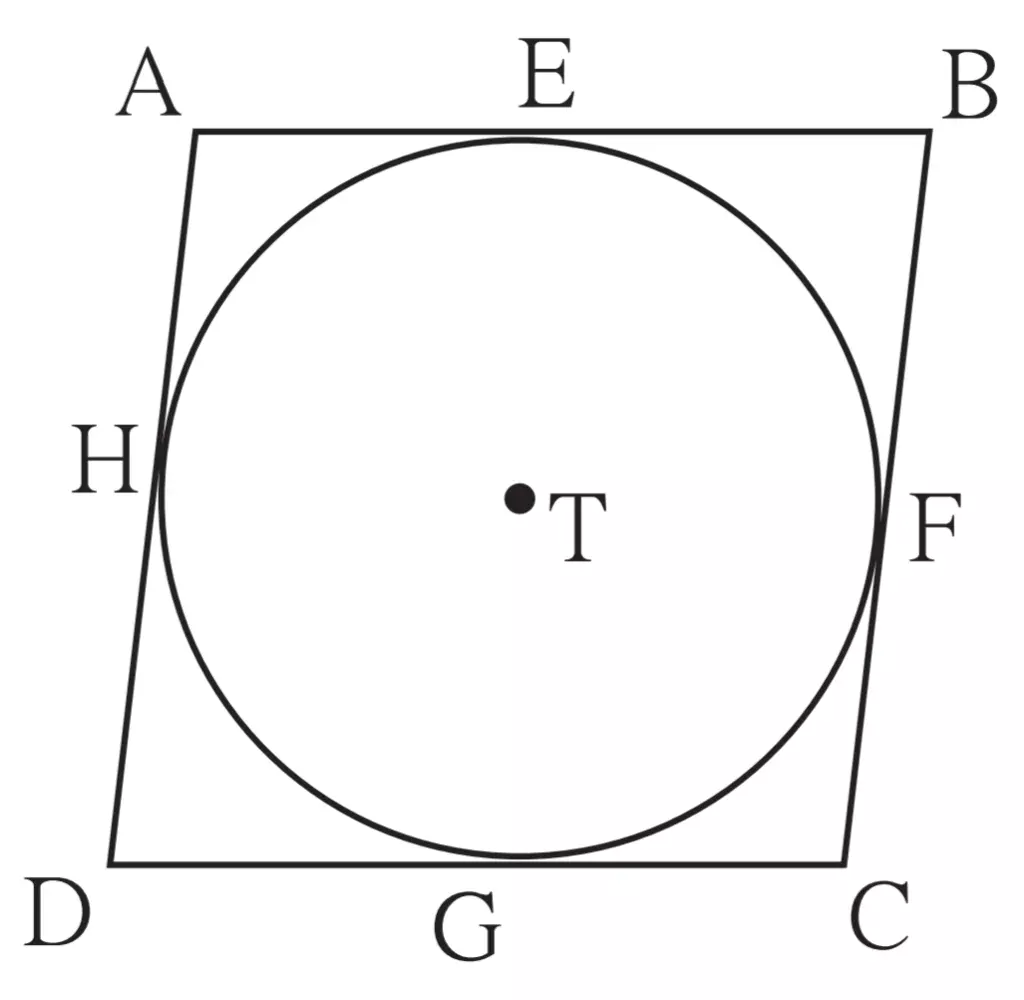
Given:
□ ABCD is a parallelogram
Points E, F, G, H are touching points
AE = 4.5
EB = 5.5
To find:
AD
Solution:
AE = AH = 4.5 …(i)
BE = BF = 5.5 …(ii) [Tangent segment of Theorem and supposition]
Let,
DH = DG = x …(iii)
CG = CF = y …(iv)
ABCD is a parallelogram …[Given]
∴ AB = CD …[Opposite sides of parallelogram are equal]
∴ AE + BE = DG + CG …[A – E – B and D – G – C]
∴ 4.5 + 5.5 = x + y …[From (i), (ii), (iii) and (iv)]
∴ x + y = 10 …(v)
∴ AD = BC …[Opposite sides of parallelogram are equal]
∴ AH + DH = BF + CF …[A – H – D and B – F – C]
∴ 4.5 + x = 5.5 + y …[From (i), (ii), (iii) and (iv)]
∴ x – y = 5.5 – 4.5
∴ x – y = 1 …(vi)
Adding (v) and (vi),
x + y + x – y = 10 + 1
∴ 2x = 11
∴ x = \(\large \frac {11}{2}\)
∴ x = 5.5
AD = AH + DH …[A – H – D]
∴ AD = 4.5 + x …[From (iii)]
∴ AD = 4.5 + 5.5 …[From (iii)]
∴ AD = 10 units
6. In figure 3.86, circle with centre M touches the circle with centre N at point T. Radius RM touches the smaller circle at S. Radii of circles are 9 cm and 2.5 cm. Find the answers to the following questions hence find the ratio MS : SR.
(1) Find the length of segment MT
(2) Find the length of seg MN
(3) Find the measure of ∠NSM.
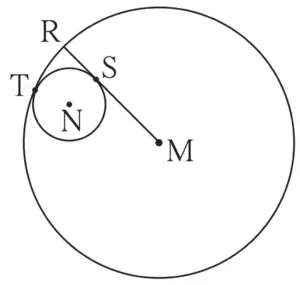
Solution:
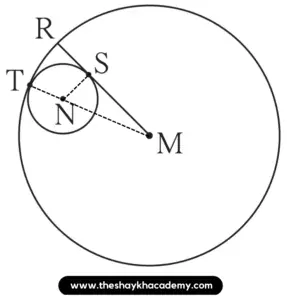
(1) MT = 9 cm …[Radius of the bigger circle]
(2) MT = MN + NT …[M – N – T]
∴ 9 = MN + 2.5
∴ MN = 9 – 2.5
∴ MN = 6.5 cm
(3) Seg MR is a tangent to the smaller circle and NS is its radius.
∴ ∠NSM = 90° …[Tangent theorem]
(4) In ∆NSM,
∠NSM = 90°
∴ MN² = NS² + MS² …[Pythagoras theorem]
∴ 6.5² = 2.5² + MS²
∴ MS² = 6.5² – 2.5²
∴ MS² = 42.25 – 6.25
∴ MS² = 36
\(\sqrt{36}\) …[Taking square root of both sides]
∴ MS = 6 cm
But,
MR = MS + SR …[M – S – R]
∴ 9 = 6 + SR
∴ SR = 9 – 6
∴ SR = 3 cm
Now,
\(\large \frac {MS}{SR}\) = \(\large \frac {6}{3}\)
\(\large \frac {MS}{SR}\) = \(\large \frac {2}{1}\)
∴ MS : SR = 2 : 1
7. In the adjoining figure circles with centres X and Y touch each other at point Z. A secant passing through Z intersects the circles at points A and B respectively. Prove that, radius XA || radius YB. Fill in the blanks and complete the proof.
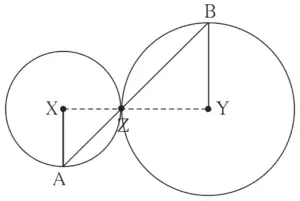
Construction:
Draw segments XZ and ………. .
Proof:
By theorem of touching circles, points X, Z, Y are ………. .
∴ ∠XZA ≅ ………. opposite angles
Let ∠XZA = ∠BZY = a …(I)
Now, seg XA ≅ seg XZ …(……….)
∴ ∠XAZ = ………. = a …(isosceles triangle theorem) (II)
Similarly, seg YB ≅ ………. …(……….)
∴ ∠BZY = ………. = a …(……….) (III)
∴ from (I), (II), (III),
∠XAZ = ……….
∴ radius XA || radius YB …(……….)
Solution:
Construction:
Draw segments XZ and seg YZ
Proof:
By theorem of touching circles, points X, Z, Y are collinear points.
∴ ∠XZA ≅ ∠BZY opposite angles
Let ∠XZA = ∠BZY = a …(I)
Now, seg XA ≅ seg XZ …(Radii of the same circle)
∴ ∠XAZ = ∠XZA = a …(isosceles triangle theorem) (II)
Similarly, seg YB ≅ seg YZ …(Radii of the same circle)
∴ ∠BZY = ∠YBZ = a …(Isosceles triangle theorem) (III)
∴ from (I), (II), (III),
∠XAZ = ∠YBZ
∴ radius XA || radius YB …(Converse of alternate angles test)
8. In figure 3.88, circles with centres X and Y touch internally at point Z . Seg BZ is a chord of bigger circle and it intersects smaller circle at point A. Prove that, seg AX || seg BY.
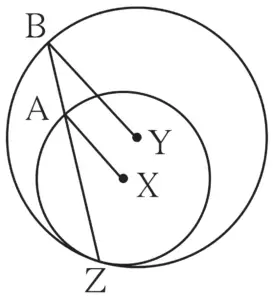
Solution:
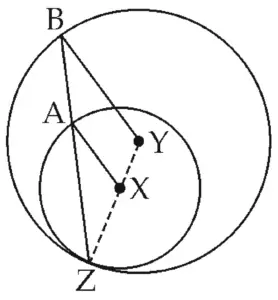
Given:
X and Y are the centres of the circle.
To prove:
seg AX || seg BY
Proof:
In ∆XAZ,
seg XA ≅ seg XZ …[Radii of the same circle]
∴ ∠XZA ≅ ∠XAZ …(i) [Isosceles triangle theorem]
Also,
In ∆YBZ,
seg YB ≅ seg YZ …[Radii of the sanie circle]
∴ ∠YZB ≅∠YBZ …[Isosceles triangle theorem]
∴ ∠XZA ≅ ∠YBZ …(ii) [Y – X – Z,B – A – Z]
∴ ∠XAZ ≅ ∠YBZ …[From (i) and (ii)]
∴ seg AX || seg BY …[Corresponding angles test]
Hence proved.
9. In figure 3.89, line l touches the circle with centre O at point P. Q is the midpoint of radius OP. RS is a chord through Q such that chords RS || line l. If RS = 12, find the radius of the circle.
Solution:
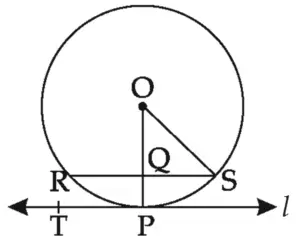
Take a point T on line l as shown in the figure.
∠OPT = 90⁰ …(i) [Tangent Theorem]
chord RS || line l …[Given]
∴ ∠OPT ≅ ∠OQR …(ii) [Corresponding angles theorem]
∴ ∠OQR = 90⁰ …(iii) [From (i) and (ii)]
∴ seg OQ ⊥ chord RS …[From (iii)]
∴ QR = \(\large \frac {1}{2}\) × RS …[Perpendicular drawn from the centre of the circle to the chord bisects the chord.]
∴ QR = \(\large \frac {1}{2}\) × 12
∴ QR = 6 units
Let the radius of the circle be x units.
∴ OR = OP = x units …[Radii of the same circle]
∴ OQ = \(\large \frac {1}{2}\) OP [∵ Q is midpoint of seg OP]
∴ OQ = \(\large \frac {1}{2}\) × x
∴ OQ = \(\large \frac {x}{2}\)
In ∆OQR,
∠OQR = 90⁰ … [From (iii)]
∴ OR² = OQ² + QR2² …[By Pythagoras theorem]
∴ x² = \(\large (\frac {x}{2})^2\) + (6)²
∴ x² = \(\large \frac {x}{4}\) + (6)²
∴ 4x = x² + 144 …[Multiplying throughout by 4]
∴ 4x² – x² = 144
∴ 3x² = 144
∴ x² = \(\large \frac {144}{3}\)
∴ x² = 48
∴ x = \(\sqrt{48}\) …[Taking square roots]
∴ x = \(\sqrt{16\,×\,3}\)
∴ x = 4\(\sqrt{3}\)
∴ OR = OP = 4\(\sqrt{3}\)units
Ans: Radius of the circle is 4\(\sqrt{3}\) units.
10. In figure 3.90, seg AB is a diameter of a circle with centre C. Line PQ is a tangent, which touches the circle at point T. seg AP ⊥ line PQ and seg BQ ⊥ line PQ. Prove that, seg CP ≅ seg CQ.
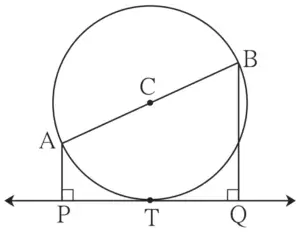
Given:
Seg AB is a diameter
Line PQ is a tangent, which touches the circle at point T
Seg AP ⊥ line PQ
Seg BQ ⊥ line PQ
Construction:
Draw seg CT, seg CP and seg CQ.
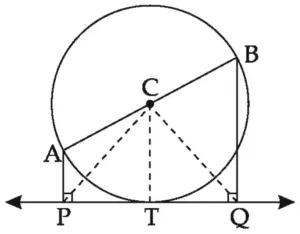
Proof:
seg AP ⊥ line PQ …(i) [Given]
seg CT ⊥ line PQ …(ii) [Tangent Theorem]
seg BQ ⊥ line PQ …(iii) [Given]
∴ seg AP seg CT seg BQ …[Perpendicular drawn to the same line are parallel to each other from (i), (ii) and (iii)]
On transversals AB and PQ,
\(\large \frac {PT}{QT}\) = \(\large \frac {AC}{BC}\) …(iv) [Property of intercepts made by three parallel lines]
But, AC = BC …[Radii of the same circle]
∴ \(\large \frac {AC}{BC}\) = 1 …(v)
∴ \(\large \frac {PT}{QT}\) = 1 …(vi) [From (iv) and (v)]
∴ PT = QT …(vi)
In ∆PTC and ∆QTC,
seg CT ≅ seg CT …[Common side]
∠CTP ≅ ∠CTQ …[Each is 90⁰, from (ii)]
seg PT ≅ seg QT ...[From (vi)]
∴ ∆PTC ≅ ∆QTC …[By SAS test of congruency]
∴ seg CP ≅ seg CQ …[c.s.c.t.]
Hence proved.
11. Draw circles with centres A, B and C each of radius 3 cm, such that each circle touches the other two circles.
Solution:
Draw an equilateral triangle ABC with each side measuring 6 cm. Taking A as centre draw a circle with a radius of 3 cm. Repeat the same thing, taking B and C as centres.
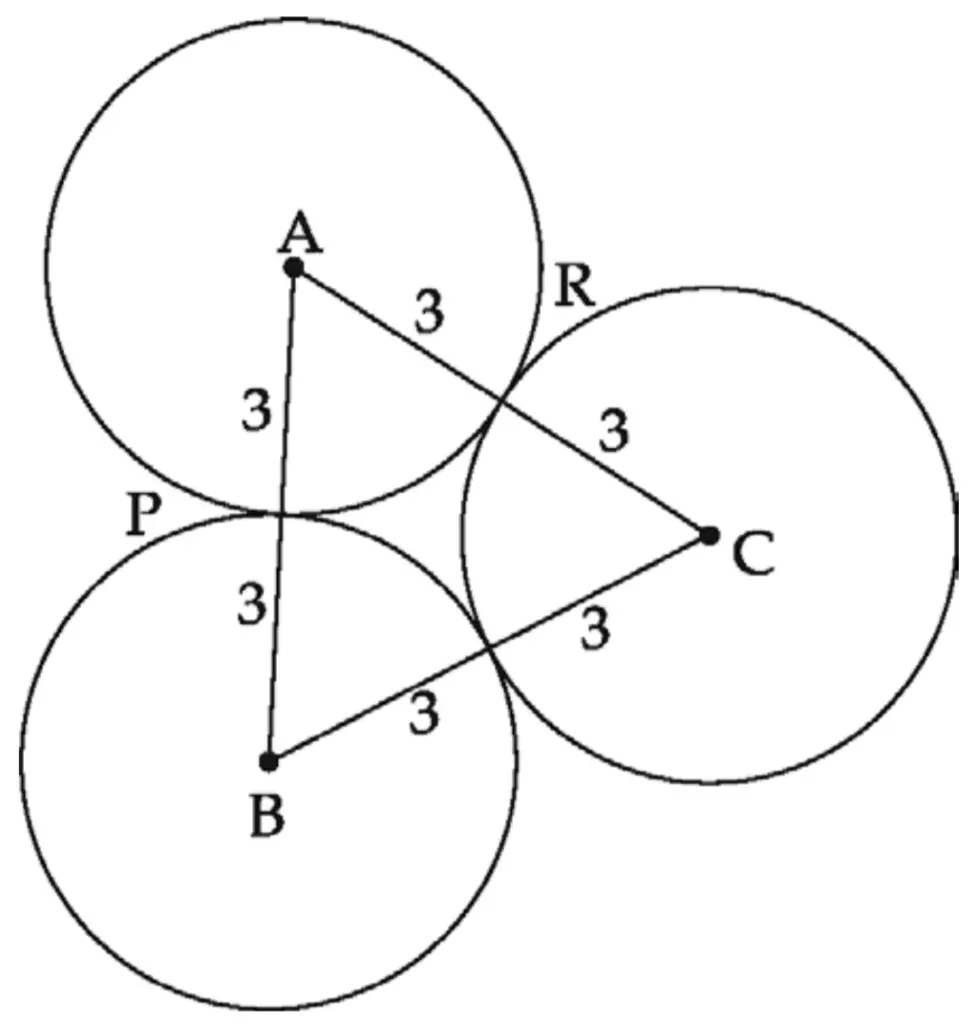
A – P – B
B – Q – C
C – R – A …[For two touching circles point of contact lies on the line joining the centres]
12. Prove that any three points on a circle cannot be collinear.
Given:
Circle with centre O.
Points A, B and C lie on the circle.
To prove:
Points A, B and C are not collinear.
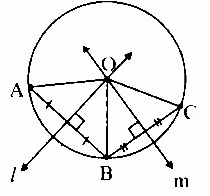
Proof:
OA = OB …[Radii of the same circle]
∴ Point O is equidistant from the endpoints A and B of seg AB.
∴ Point O lies on the perpendicular bisector of AB …[Perpendicular bisector theorem]
Similarly, we can prove that,
Point O lies on the perpendicular bisector of BC.
∴ Point O is the point of intersection of perpendicular bisectors of AB and BC …(i)
Now,
Suppose that the points A, B, C are collinear.
Then, the perpendicular bisector of AB and BC will be parallel …[Perpendiculars to the same line are parallel]
∴ The perpendicular bisector do not intersect at O.
This contradicts statement (i) that the perpendicular bisectors intersect each other at O.
Our supposition that A, B, C are collinear is false.
∴ Points A, B and C are non collinear points.
13. In figure 3.91, line PR touches the circle at point Q. Answer the following questions with the help of the figure.
(1) What is the sum of ∠TAQ and ∠TSQ?
(2) Find the angles which are congruent to ∠AQP.
(3) Which angles are congruent to ∠QTS?
(4) ∠TAS = 65°, find the measure of ∠TQS and arc TS.
(5) If ∠AQP = 42°and ∠SQR = 58° find measure of ∠ATS.
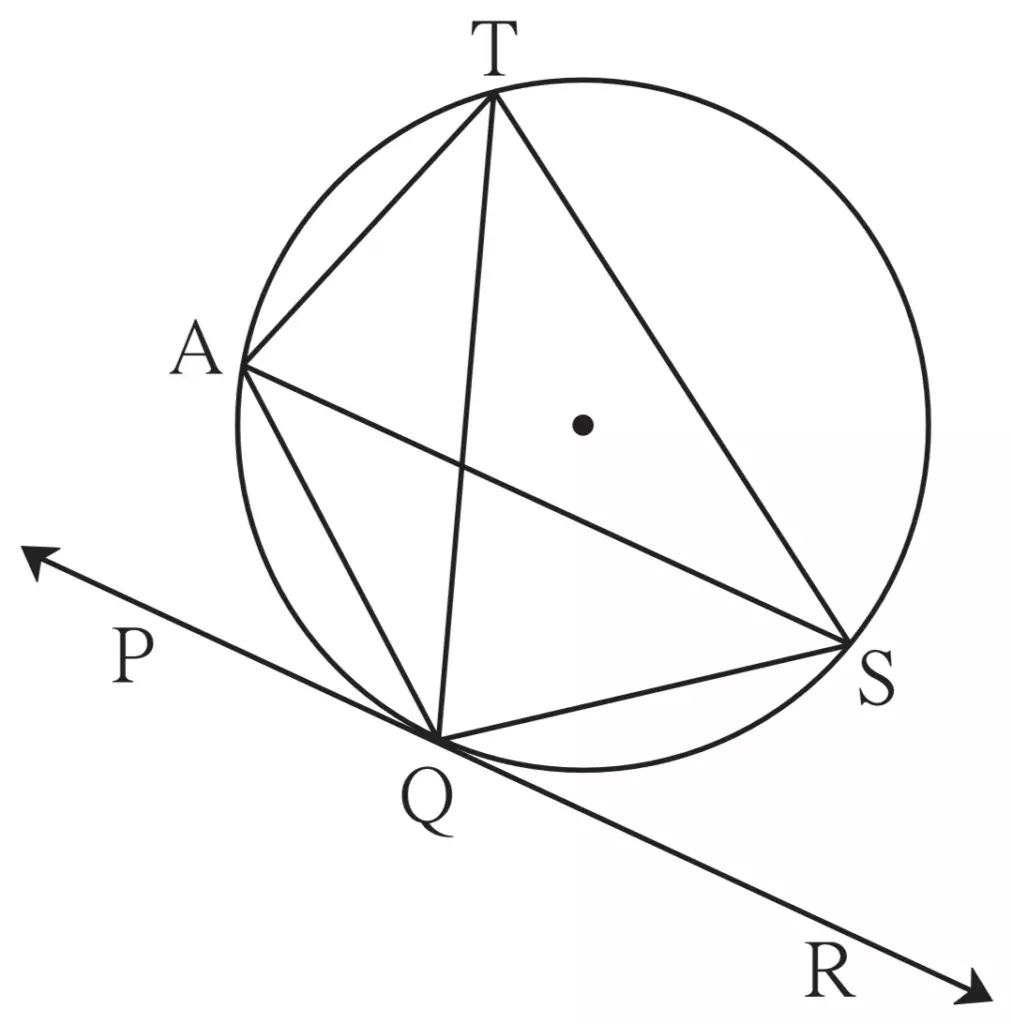
Solution:
(i) □ TAQS is a cyclic quadrilateral …[Definition]
∴ ∠TAQ + ∠TSQ = 180° …[Cyclic quadrilateral theorem]
(ii) ∠ATQ ≅ ∠AQP …[Angles in alternate segments]
∠ASQ ≅ ∠AQP
(iii) ∠QAS ≅ ∠QTS …[Angles inscribed in the same arc]
∠RQS ≅ ∠QTS …[Angles in alternate segment]
(iv) ∠TQS ≅ ∠TAS …[Angles inscribed in the same arc]
∠TAS = 65° …[Given]
∴ ∠TQS = 65°
∠TQS = \(\large \frac {1}{2}\) m(arc TS) …[Inscribed angle theorem]
∴ 65° = \(\large \frac {1}{2}\) m(arc TS)
∴ m(arc TS) = 65° × 2
∴ m(arc TS) = 130°
(v) ∠ATQ ≅ ∠AQP …[Angles in alternate segments]
∴ ∠ATQ = 42° …(i)
∠STQ ≅ ∠SQR …[Angles in alternate segments]
∴ ∠STQ = 58° …(ii)
∠ATS = ∠ATQ + ∠STQ …[Angle addition property]
∠ATS = 42° + 58° …[From (i) and (ii)]
∴ ∠ATS = 100°
14. In figure 3.92, O is the centre of a circle, chord PQ ≅ chord RS. If ∠POR = 70°and (arc RS) = 80°, find
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)
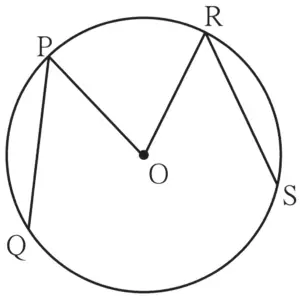
Given:
O is the centre of the circle
chord PQ ≅ chord RS
∠POR = 70°
arc RS = 80°
To find:
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)
Solution:
m (arc PR) = m∠POR …[Definition of measure of minor arc]
∴ m (arc PR) = 70⁰ …(i)
chord PQ ≅ chord RS …[Given]
∴ arc PQ ≅ arc RS …[In a circle, congruent chords have corresponding minor arcs congruent]
∴ m (arc PQ) = 80⁰ …(ii)
m (arc PR) + m (arc RS) + m (arc PQ) + m (arc QS) = 360⁰ …[Measure of circle]
∴ 70⁰ + 80⁰ + 80⁰ + m (arc QS) = 360⁰
∴ m (arc QS) = 360⁰ – 230⁰
∴ m (arc QS) = 130⁰ …(iii)
m (arc QSR) = m (arc QS) + m (arc SR) …[Arc addition property]
∴ m (arc QSR) = 130⁰ + 80⁰
∴ m (arc QSR) = 210⁰
15. In figure 3.93, m(arc WY) = 44°, m(arc ZX) = 68°, then
(1) Find the measure of ∠ZTX.
(2) If WT = 4.8, TX = 8.0, YT = 6.4, find TZ.
(3) If WX = 25, YT = 8, YZ = 26, find WT.
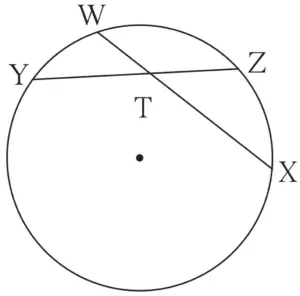
Given:
m(arc WY) = 44°
m(arc ZX) = 68°
To find:
(1) Find the measure of ∠ZTX.
(2) If WT = 4.8, TX = 8.0, YT = 6.4, find TZ.
(3) If WX = 25, YT = 8, YZ = 26, find WT.
Solution:
(1) m∠ZTX = \(\large \frac {1}{2}\) × [m (arc WY) + m(arc ZX)]
∴ m∠ZTX = \(\large \frac {1}{2}\) × [44 + 68]
∴ m∠ZTX = \(\large \frac {1}{2}\) × 112
∴ m∠ZTX = 56°
(2) WT × TX = TZ × YT …[Theorem on internal division of chords]
∴ 4.8 × 8 = TZ × 6.4
∴ 38.4 = TZ × 6.4
∴ TZ = \(\large \frac {38.4}{6.4}\)
∴ TZ = 6 units
(3) WX = WT + TX …[W – T – X]
∴ 12.8 = WT + 6.4
∴ WT = 12.8 – 6.4
∴ WT = 6.4 units
16. In figure 3.94,
(1) m(arc CE) = 54°, m(arc BD) = 23°, find measure of ∠CAE.
(2) If AB = 4.2, BC = 5.4, AE = 12.0, find AD
(3) If AB = 3.6, AC = 9.0, AD = 5.4, find AE
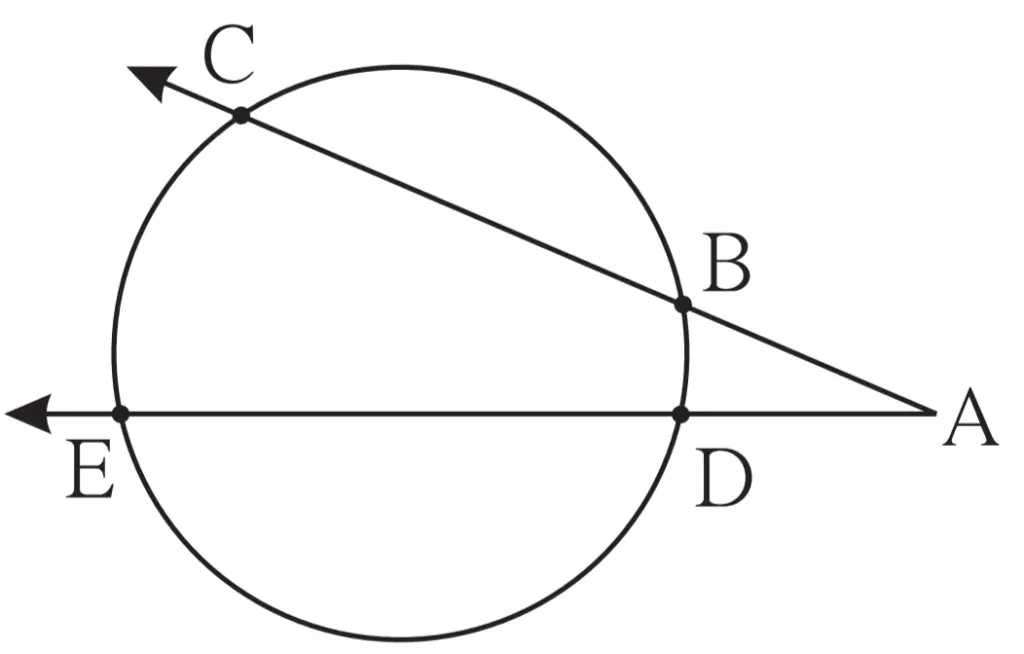
Solution:
(i) ∠CAE = \(\large \frac {1}{2}\) [m (arc CE) – m(arc BD)]
∴ ∠CAE = \(\large \frac {1}{2}\) (54 – 23)
∴ ∠CAE = \(\large \frac {1}{2}\) × 31
∴ ∠CAE = 15.5°
(ii) AC = AB + BC
∴ AC = 4.2 + 5.4
∴ AC = 9.6
AD × AE = AB × AC …[Theorem of external division of chords]
∴ AD × 12 = 4.2 × 9.6
∴ 12AD = 40.32
∴ AD = \(\large \frac {40.32}{12}\)
∴ AD = 3.36 units
(iii) AE × AD = AC × AB …[Theorem of external division of chords]
∴ AE × 5.4 = 9 × 3.6
∴ AE × 5.4 = 32.4
∴ AE = \(\large \frac {32.4}{5.4}\)
∴ AE = 6 units
17. In figure 3.95, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.
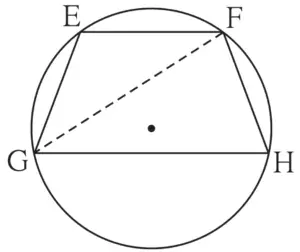
Proof :
Draw seg GF.
∠EFG = ∠FGH ………. (I)
∠EFG = ……. inscribed angle theorem (II)
∠FGH = ……. inscribed angle theorem (III)
∴ m(arc EG) = from (I), (II), (III)
chord EG ≅ chord FH ……….
Solution:
Proof :
Draw seg GF.
∠EFG = ∠FGH (Alternate angles theorem) (I)
∠EFG = \(\large \frac {1}{2}\) m(arc EG) inscribed angle theorem (II)
∠FGH = \(\large \frac {1}{2}\) m(arc FH) inscribed angle theorem (III)
∴ m(arc EG) = m(arc FH) from (I), (II), (III)
chord EG ≅ chord FH (In a circle, congruent arcs have their corresponding chords congruent)
18. In figure 3.96 P is the point of contact.
(1) If m(arc PR) = 140°, ∠POR = 36°, find m(arc PQ)
(2) If OP = 7.2, OQ = 3.2, find OR and QR
(3) If OP = 7.2, OR = 16.2, find QR.
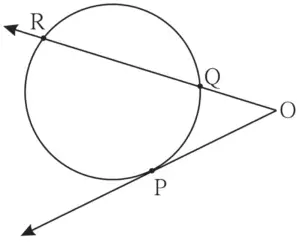
Solution:
(1) ∠POR = \(\large \frac {1}{2}\) [m(arc PR) – m(arc PQ)]
∴ 36° = \(\large \frac {1}{2}\) [140° – m(arc PQ)]
∴ 36 × 2 = 140° – m(arc PQ)
∴ m(arc PQ) = 140° – 72°
∴ m(arc PQ) = 68°
(2) OP² = OQ × OR …[Tangent secant segment theorem]
∴ 7.2 × 7.2 = 3.2 × OR
∴ 51.84 = 3.2 × OR
∴ OR = \(\large \frac {51.84}{3.2}\)
∴ OR = 16.2 units
OR = OQ + QR …[O – Q – R]
∴ 16.2 = 3.2 + QR
∴ QR = 16.2 – 3.2
∴ QR = 13 units
(3) OP² = OQ × OR …[Tangent secant segment theorem]
∴ 7.2 × 7.2 = OQ × 16.2
∴ 51.74 = OQ × 16.2
∴ OQ = \(\large \frac {51.84}{16 2}\)
∴ OQ = 3.2
OQ + QR = OR …[O – Q – R]
∴ 3.2 + QR = 16.2
∴ QR = 16.2 – 3.2
∴ QR = 13 units
19. In figure 3.97, circles with centres C and D touch internally at point E. D lies on the inner circle. Chord EB of the outer circle intersects inner circle at point A. Prove that, seg EA ≅ seg AB.
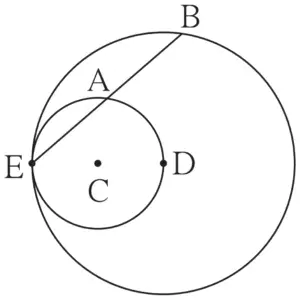
Construction:
Draw seg DE and seg DA
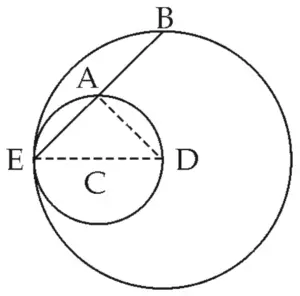
Proof:
E – C – D …[Theorem on touching circles]
Seg DE is the diameter …[Definition]
∠DAE = 90° …(i) [Diameter subtends a right angle at any point of circle other than its end points]
Consider circle with centre D.
∴ seg DA ⊥ chord BE …[From (i)]
∴ seg EA ≅ seg AB …[Perpendicular drawn from the centre to the chord bisects the chord]
20. In figure 3.98, seg AB is a diameter of a circle with centre O . The bisector of ∠ACB intersects the circle at point D. Prove that, seg AD ≅ seg BD. Complete the following proof by filling in the blanks
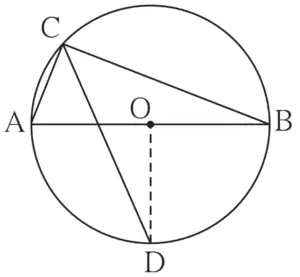
Proof:
Draw seg OD.
∠ACB = ………. angle inscribed in semicircle
∠DCB = ………. CD is the bisector of ∠ C
m(arc DB) = ………. inscribed angle theorem
∠DOB = ………. definition of measure of an arc (I)
seg OA ≅ seg OB ………. (II)
∴ line OD is of seg AB ………. From (I) and (II)
∴ seg AD ≅ seg BD
Solution:
Proof:
Draw seg OD.
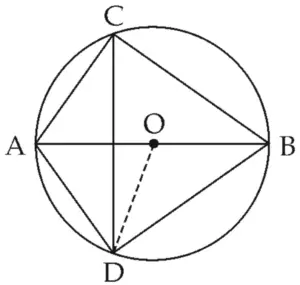
∠ACB = 90⁰ ………. angle inscribed in semicircle
∠DCB = 45⁰ ………. CD is the bisector of ∠C
m(arc DB) = 90⁰ ………. inscribed angle theorem
∠DOB = 90⁰ ………. definition of measure of an arc (I)
seg OA ≅ seg OB ………. (Radii of same circle) (II)
∴ line OD is perpendicular bisector of seg AB ………. From (I) and (II)
∴ seg AD ≅ seg BD
21. In figure 3.99, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
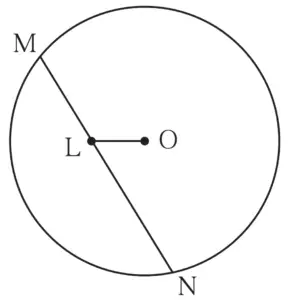
Construction:
Draw seg OM and seg OA ⊥ chord MN …[M – A – N]
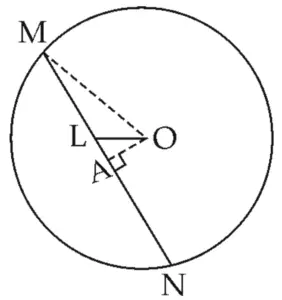
Solution:
Seg OA ⊥ chord MN …[Construction]
∴ MA = \(\large \frac {1}{2}\) × MN …[Perpendicular drawn from the centre to the chord bisects the chord]
∴ MA = \(\large \frac {1}{2}\) × 25
∴ MA = 12.5 units …(i)
MA = ML + LA …[M – L – A]
∴ 12.5 = 9 + LA …[From (i) and given]
∴ 12.5 – 9 = LA
∴ LA = 3.5 units …(ii)
In ∆OAL,
∠OAL = 90° …[Construction]
\ OL² = OA² + LA² …[Pythagoras theorem]
∴ 5² = OA² + (3.5)² …[From (ii) and given]
∴ OA² = 25 – 12.25
∴ OA² = 12.75 …(iii)
In ∆OAM,
∠OAM = 90° …[Construction]
∴ OM² = OA² + MA²…[Pythagoras theorem]
∴ OM² = 12.75 + (12.5)² …[From (iii) and given]
∴ OM² = 12.75 + 156.25
∴ OM² = 169
∴ OM = 13 units …[Taking square roots]
Ans: Radius of the circle is 13 units
22. In figure 3.100, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P, Q. Prove that, ∠PRQ + ∠PSQ = 180°
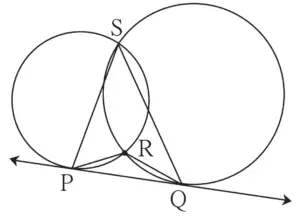
Given:
Circles intersect at points S and R.
Common tangent PQ touches the circle at points P, Q
Prove that:
∠PRQ + ∠PSQ = 180°
Construction:
Draw seg RS
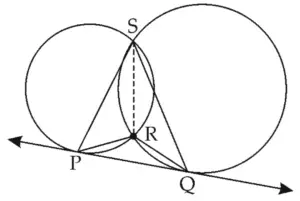
Proof:
∠PSR ≅ ∠RPQ …(i)
∠QSR ≅ ∠RQP …(ii) [Angles in alternate segments]
In ∆PRQ,
∠PRQ + ∠RPQ + ∠RQP = 180° …[Sum of angles of a triangle is 180°]
∴ ∠PRQ + ∠PSR + ∠QSR = 180° …[From (i) and (ii)]
∴ ∠PRQ + ∠PSQ = 180° …[Angle addition property]
23. In figure 3.101, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R, S and P, Q respectively. Prove that : seg SQ || seg RP.
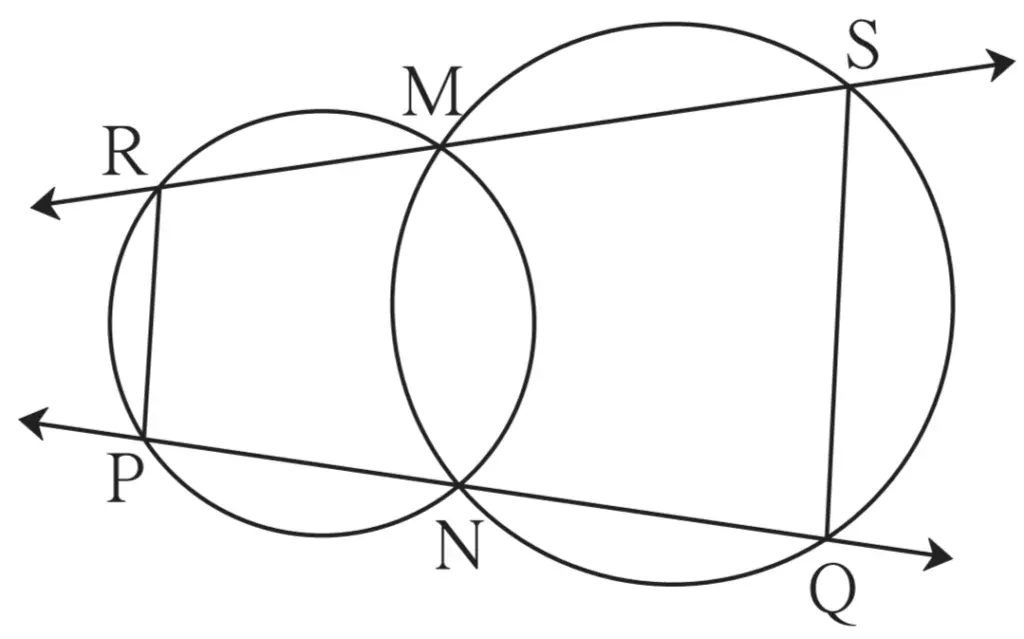
Given:
Two circles intersect at points M and N
Secants drawn through M and N intersect the circles at points R, S and P, Q respectively.
To Prove:
seg PR || seg QS
Construction:
Draw seg MN
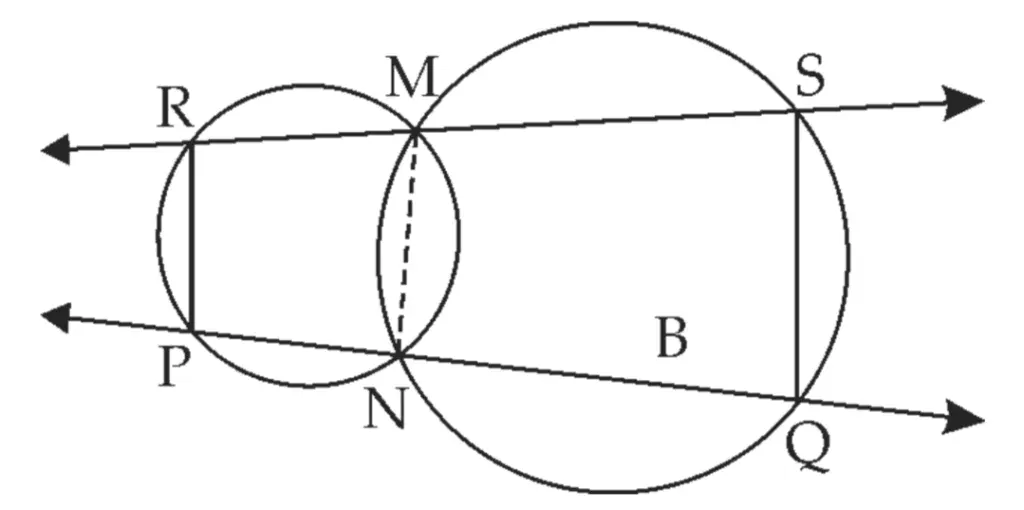
Proof:
□ PNMR is a cyclic quadrilateral …[Definition]
∠MNQ is an exterior angle of □ PNMR …[Definition]
∴ ∠MNQ ≅ ∠PRM …(i)
□ MNQS is cyclic quadrilateral …[Definition]
∴ ∠MNQ + ∠MSQ = 180° …(ii) [Opposite angles of a cyclic quadrilateral are supplementary]
∴ ∠PRM + ∠MSQ = 180° …[From (i) and (ii)]
∴ ∠PRS + ∠RSQ = 180° …[R – M – S]
∴ seg PR || seg QS …[Interior angles test]
Hence proved.
24. In figure 3.102, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that □ ABCD is cyclic.
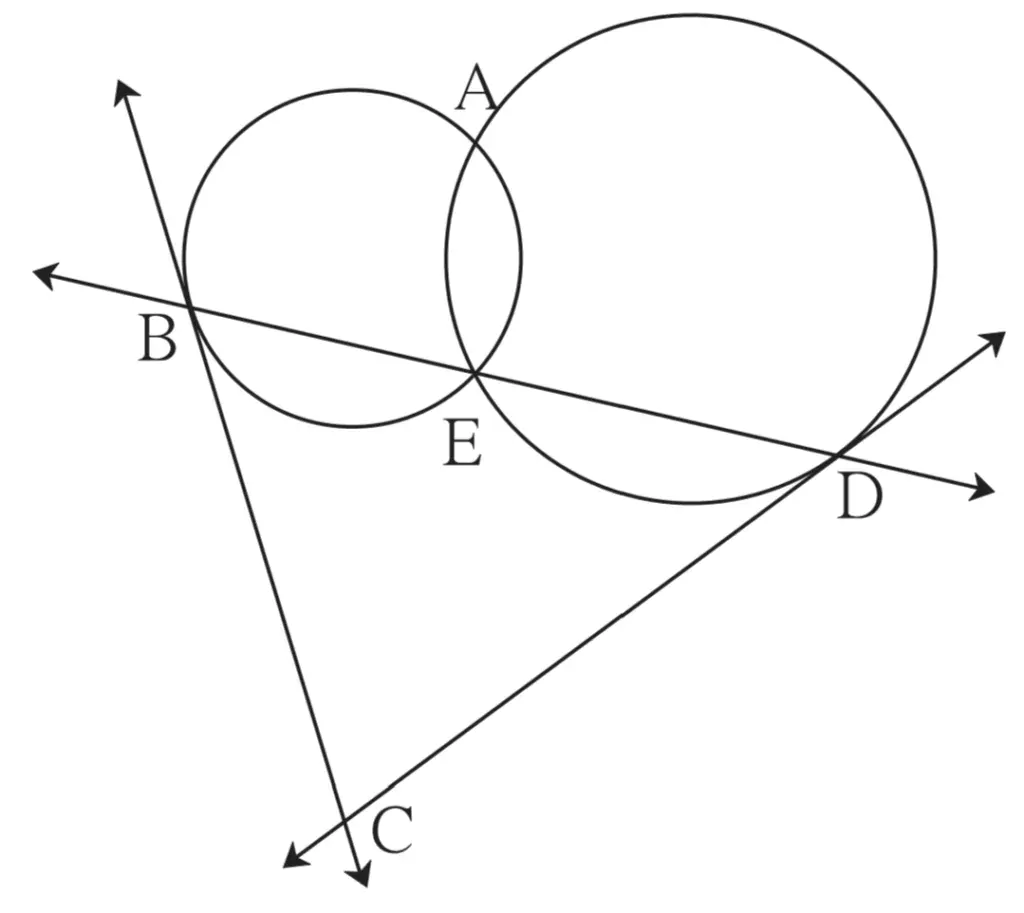
To Prove:
□ ABCD is a cyclic quadrilateral
Proof:
∠BAE ≅ ∠EBC …(i)
∠DAE ≅ ∠EDC …(ii) [Angles in alternate segments]
In ∆BCD,
∠BCD + ∠DBC + ∠BDC = 180° …[Sum of angle of a triangle is 180°]
∴ ∠BCD + ∠EBC + ∠EDC = 180° …[B – E – D]
∠BCD + ∠BAE + ∠DAE = 180° …[From (i) & (ii)]
∠BCD + ∠BAD = 180° …[Angle addition property]
∴ □ ABCD is a cyclic quadrilateral …[Converse of cyclic quadrilateral Theorem]
Hence proved.
25. In figure 3.103, seg AD ⊥ side BC, seg BE ⊥ side AC, seg CF ⊥ side AB. Point O is the orthocentre. Prove that , point O is the incentre of ∆DEF.
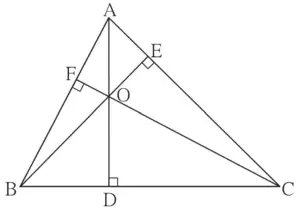
Given:
seg AD ⊥ side BC
seg BE ⊥ side AC
seg CF ⊥ side AB.
To prove:
Point O is the incentre of ∆DEF.
Construction:
Draw DE, EF and DF.
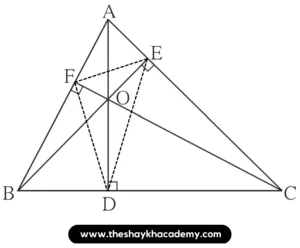
Proof:
∠OFA ≅ ∠OEA = 90° …[Given]
∴ ∠OFA + ∠OEA = 90° + 90°
∴ ∠OFA + ∠OEA = 180°
∴ □ OFAE is a cyclic quadrilateral …[Converse of cyclic quadrilateral theorem]
∴ Points O, F, A, E are concyclic points.
seg OE subtends equal angles ∠OFE and ∠OAE on the same side of OE.
∴ ∠OFE ≅ ∠OAE …(i)
∠OFB ≅ ∠ODB = 90° …[Given]
∴ ∠OFB + ∠ODB = 90° + 90°
∴ ∠OFB + ∠ODB = 180°
∴ OFBD is a cyclic quadrilateral …[Converse of cyclic quadrilateral theorem]
∴ Points O, F, B, D are concyclic points
seg OD subtends equal angles ∠OFD and ∠OBD on the same side of OD.
∴ ∠OFD ≅ ∠OBD …(ii)
In ∆AEO and ∆BDO,
∠AEO ≅ ∠BDO …[Each angle is 90°]
∠AOE = ∠BOD …[Vertically opposite angles]
∴ ∆AEO ~ ∆BDO …[AA test of similarity]
∴ ∠OAE = ∠OBD …(iii) [Corresponding angles of similar triangles]
∴ ∠OFE ≅ ∠OFD …[From (i), (ii) and (iii)]
∴ ray FO bisects ∠EFD.
Similarly,
We can prove ray EO and ray DO bisects ∠FED and ∠FDE respectively.
∴ Point O is the intersection of angle bisectors of ∠D, ∠E and ∠F of ∆DEF.
∴ Point O is the incentre of ∆DEF.
Hence proved.
