Chapter 2 – Quadratic Equations
Practice set 2.1
1. Write any two quadratic equations.
Ans: x² + 2x – 3 = 0 and 3x² – 4x + 6 = 0 are quadratic equations in variable x.
2. Decide which of the following are quadratic equations.
(1) x² + 5x – 2 = 0
Solution:
x² + 5x – 2 = 0
Here, x is the only variable and maximum index of variable x is 2.
∴ It is a quadratic equation in variable x.
(2) y² = 5y – 10
Solution:
y² = 5y – 10
∴ y² – 5y + 10 = 0
Here, y is the only variable and maximum index of variable y is 2.
∴ It is a quadratic equation in variable y.
(3) y² + \(\large \frac {1}{y}\) = 2
Solution:
y² + \(\large \frac {1}{y}\) = 2
Multiplying both sides by y we get,
y³ + y × \(\large \frac {1}{y}\) = 2y
∴ y³ + 1 = 2y
∴ y³ – 2y + 1 = 0
Here, the maximum index of the variable y is 3 and not 2.
∴ It is not a quadratic equation.
(4) x + \(\large \frac {1}{x}\) = – 2
Solution:
x + \(\large \frac {1}{x}\) = – 2
Multiplying both sides by x we get,
x² + x × \(\large \frac {1}{x}\) = – 2x
∴ x² + 1 = – 2x
∴ x² + 2x + 1 = 0
Here, x is the only variable and maximum index of variable x is 2.
∴ It is a quadratic equation in variable x.
(5) (m + 2) (m – 5) = 0
Solution:
(m + 2) (m – 5) = 0
∴ m(m – 5) + 2(m – 5) = 0
∴ m² – 5m + 2m – 10 = 0
∴ m² – 3m – 10 = 0
Here, m is the only variable and maximum index of variable m is 2.
∴ It is a quadratic equation in variable m.
(6) m³ + 3m² – 2 = 3m³
Solution:
m³ + 3m² – 2 = 3m³
∴ 3m³ – m³ – 3m² + 2 = 0
∴ 2m³ – 3m² + 2 = 0
Here, maximum index of the variable m is 3 and not 2
∴ It is not a quadratic equation in variable m.
3. Write the following equations in the form ax² + bx + c = 0, then write the values of a, b, c for each equation.
(1) 2y = 10 – y²
Solution:
2y = 10 – y²
∴ y² + 2y – 10 = 0
Comparing with ay² + by + c = 0 we get,
a = 1, b = 2, c = – 10
(2) (x – 1)² = 2x + 3
Solution:
(x – 1)² = 2x + 3
∴ x² – 2x + 1 = 2x + 3 …[Using (a – b)² = a² – 2ab + b²]
∴ x² – 2x – 2x + 1 – 3 = 0
∴ x² – 4x – 2 = 0
Comparing with ax² + bx + c = 0 we get,
a = 1, b = – 4, c = –2
(3) x² + 5x = – (3 – x)
Solution:
x² + 5x = – (3 – x)
∴ x² + 5x = – 3 + x
∴ x² + 5x – x + 3 = 0
∴ x² + 4x + 3 = 0
Comparing with ax² + bx + c = 0 we get,
a = 1, b = 4, c = 3
(4) 3m² = 2m² – 9
Solution:
3m² = 2m² – 9
3m² – 2m² + 9 = 0
m² + 9 = 0
m² + 0m + 9 = 0
Comparing with am² + bm + c = 0 we get,
a = 1, b = 0, c = 9
(5) p(3 + 6p) = – 5
Solution:
p(3 + 6p) = – 5
∴ 3p + 6p² = – 5
∴ 6p² + 3p + 5 = 0
Comparing with ap² + bp + c = 0 we get,
a = 6, b = 3, c = 5
(6) x² – 9 = 13
Solution:
x² – 9 = 13
∴ x² – 9 – 13 = 0
∴ x² – 22 = 0
∴ x² + 0x – 22 = 0
Comparing with ax² + bx + c = 0 we get,
a = 1, b = 0, c = – 22
4. Determine whether the values given against each of the quadratic equations are the roots of the equation.
(1) x² + 4x – 5 = 0 , x = 1, –1
Solution:
(i) For x = 1,
Substituting x = 1 in L.H.S., we get,
L.H.S. = (1)² + 4(1) – 5
L.H.S. = 1 + 4 – 5
L.H.S. = 5 – 5
L.H.S. = 0
And,
R.H.S. = 0
∴ L.H.S. = R.H.S.
∴ x = 1 is the root of the given quadratic equation
(ii) For x = – 1,
Substituting x = – 1 in L.H.S., we get,
L.H.S. = (– 1)² + 4(– 1) – 5
L.H.S. = 1 – 4 – 5
L.H.S. = – 8
But,
R.H.S. = 0
∴ LHS ≠ RHS
∴ x = – 1 is not the root of the given quadratic equation.
Ans: x = 1 is the root of the given quadratic equation and x = – 1 is not the root of the given quadratic equation.
(2) 2m² – 5m = 0 , m = 2, m = \(\large \frac {5}{2}\)
Solution:
(i) For m = 2,
Substituting m = 2 in L.H.S., we get,
L.H.S. = 2(2)² – 5(2)
L.H.S. = (2 × 4) – 10
L.H.S. = 8 – 10
L.H.S. = – 2
But,
R.H.S. = 2
∴ L.H.S. ≠ R.H.S.
∴ m = 2 is not the root of the given quadratic equation.
(ii) For m = \(\large \frac {5}{2}\)
Substituting m = \(\large \frac {5}{2}\) in L.H.S. we get,
L.H.S. = 2 \(\large (\frac {5}{2})²\) – 5 \(\large (\frac {5}{2})\)
L.H.S. = 2 × \(\large \frac {25}{4}\) – 5 × \(\large \frac {5}{2}\)
L.H.S. = \(\large \frac {25}{2}\) – \(\large \frac {25}{2}\)
L.H.S. = 0
And,
R.H.S. = 0
∴ m = \(\large \frac {5}{2}\) is the root of the given quadratic equation.
Ans: m = 2 is not the root of the given quadratic equation and m = \(\large \frac {5}{2}\) is the root of the given quadratic equation.
5. Find k if x = 3 is a root of equation kx² – 10x + 3 = 0.
Solution:
x = 3 is one of the roots of the given quadratic equation.
∴ It satisfies the given equation.
Substituting x = 3 in the given quadratic equation, we get,
∴ k(3)² – 10(3) + 3 = 0
∴ 9k – 30 + 3 = 0
∴ 9k – 27 = 0
∴ 9k = 27
∴ k = \(\large \frac {27}{9}\)
∴ k = 3
Ans: The value of k is 3.
6. One of the roots of equation 5m² + 2m + k = 0 is \(\large \frac {–\,7}{5}\). Complete the following activity to find the value of ‘k’.
Solution:
□ is a root of quadratic equation 5m² + 2m + k = 0
∴ Put m = □ in the equation.
5 × □² + 2 × □ + k = 0
□ + □ + k = 0
□ + k = 0
k = □
Solution:
\(\large \frac {–\,7}{5}\) is a root of quadratic equation 5m² + 2m + k = 0
∴ Put m = \(\large \frac {–\,7}{5}\) in the equation.
5 × \((\large \frac {–\,7}{5})²\) + 2 × \(\large \frac {–\,7}{5}\) + k = 0
\(\large \frac {49}{5}\) + \((\large \frac {–\,14}{5})\) + k = 0
7 + k = 0
k = – 7
Practice set 2.2
1. Solve the following quadratic equations by factorisation.
(1) x² – 15 x + 54 = 0
Solution:
x² – 15x + 54 = 0
x² – 9x – 6x + 54 = 0
x(x – 9) – 6(x – 9) = 0
(x – 9) (x – 6) = 0
x – 9 = 0 or x – 6 = 0
x = 9 or x = 6
Ans: The roots of the given quadratic equation are 9 and 6.
(2) x² + x – 20 = 0
Solution:
x² + x – 20 = 0
x² + 5x – 4x – 20 = 0
x(x + 5) – 4(x + 5) = 0
(x + 5) (x – 4) = 0
x + 5 = 0 or x – 4 = 0
x = –5 or x = 4
Ans: The roots of the given quadratic equation are – 5 and 4.
(3) 2y² + 27 y + 13 = 0
Solution:
2y² + 27y + 13 = 0
2y² + 26y + y + 13 = 0
2y(y + 13) + 1(y + 13) = 0
(y + 13) (2y + 1) = 0
y + 13 = 0 or 2y + 1 = 0
y = – 13 or 2y = – 1
y = – 13 or y = – \(\large \frac {1}{2}\)
Ans: The roots of given quadratic equation are –13 or – \(\large \frac {1}{2}\).
(4) 5m² = 22 m + 15
Solution:
5m² = 22m + 15
5m² – 22m – 15 = 0
5m² – 25m + 3m – 15 = 0
5m(m – 5) + 3(m – 5) = 0
(m – 5) (5m + 3) = 0
m – 5 = 0 or 5m + 3 = 0
m = 5 or 5m = –3
m = 5 or m = – \(\large \frac {3}{5}\)
Ans: The roots of given quadratic equation are 5 or – \(\large \frac {3}{5}\).
(5) 2x² – 2 x + \(\large \frac {1}{2}\) = 0
Solution:
2x² – 2x + \(\large \frac {1}{2}\) = 0
Multiplying throughout by 2, we get
4x² – 4x + 1= 0
4x² – 2x – 2x + 1= 0
2x(2x – 1) – 1(2x – 1) = 0
(2x – 1) (2x – 1) = 0
2x – 1 = 0 or 2x – 1 = 0
2x = 1 or 2x = 1
x = \(\large \frac {1}{2}\) or x = \(\large \frac {1}{2}\)
Ans: The root of given quadratic equation are – \(\large \frac {1}{2}\) or \(\large \frac {1}{2}\).
(6) 6x – \(\large \frac {2}{x}\) = 1
Solution:
6x – \(\large \frac {2}{x}\) = 1
Multiplying both the sides by x, we get
6x² – 2 = x
6x² – x – 2 = 0
6x² – 4x + 3x – 2 = 0
2x (3x – 2) + 1(3x – 2) = 0
(3x – 2) (2x + 1) = 0
3x – 2 = 0 or 2x + 1 = 0
3x = 2 or 2x = –1
x = \(\large \frac {2}{3}\) or x = − \(\large \frac {1}{2}\)
Ans: The roots of the given quadratic equation are x = \(\large \frac {2}{3}\) or x = − \(\large \frac {1}{2}\).
(7) \(\sqrt{2}\) x² + 7x + 5 \(\sqrt{2}\) = 0 to solve this quadratic equation by factorisation, complete the following activity.
Solution:
\(\sqrt{2}\) x² + 7x + 5 \(\sqrt{2}\) = 0
\(\sqrt{2}\) x² + □ + □ + 5 \(\sqrt{2}\) = 0
x( ____ ) + \(\sqrt{2}\) ( ____ ) = 0
( ____ )(x + \(\sqrt{2}\)) = 0
( ____ ) = 0 or (x + \(\sqrt{2}\)) = 0
∴ x = ____ or x = – \(\sqrt{2}\)
∴ ____ and – 2 are the roots of the equation.
Solution:
\(\sqrt{2}\) x² + 7x + 5 \(\sqrt{2}\) = 0
\(\sqrt{2}\) x² + 5x + 2x + 5 \(\sqrt{2}\) = 0
x(\(\sqrt{2}\) + 5 ) + \(\sqrt{2}\) (\(\sqrt{2}\) + 5) = 0
(\(\sqrt{2}\) + 5)(x + \(\sqrt{2}\)) = 0
\(\sqrt{2}\) + 5 = 0 or (x + \(\sqrt{2}\)) = 0
∴ x = – \(\large \frac {5}{\sqrt{2}}\) or x = – \(\sqrt{2}\)
∴ – \(\large \frac {5}{\sqrt{2}}\) and – 2 are the roots of the equation.
(8) 3x² – 2 \(\sqrt{6}\) x + 2 = 0
Solution:
3x² – 2 \(\sqrt{6}\) x + 2 = 0
3x² – \(\sqrt{6}\) x – \(\sqrt{6}\) x + 2 = 0
\(\sqrt{3}\) × (\(\sqrt{3}\) x – \(\sqrt{2}\)) – 2 (\(\sqrt{3}\) x – \(\sqrt{2}\)) = 0
(\(\sqrt{3}\) x – \(\sqrt{2}\)) (\(\sqrt{3}\) x – \(\sqrt{2}\)) = 0
\(\sqrt{3}\) x – \(\sqrt{2}\) = 0 or \(\sqrt{3}\) x – \(\sqrt{2}\) = 0
x = \(\large \frac {\sqrt{2}}{\sqrt{3}}\) or x = \(\large \frac {\sqrt{2}}{\sqrt{3}}\)
Ans: The root of given quadratic equation are \(\large \frac {\sqrt{2}}{\sqrt{3}}\) and \(\large \frac {\sqrt{2}}{\sqrt{3}}\).
(9) 2m(m – 24) = 50
Solution:
2m(m – 24) = 50
2m² – 48m = 50
2m² – 48m – 50 = 0
m² – 24m – 25 = 0 …[Dividing both sides by 2]
m² – 25m + m – 25 = 0
m(m – 25) +1(m – 25) = 0
(m – 25) (m + 1) = 0
m – 25 = 0 or m + 1 = 0
m = 25 or m = – 1
Ans: The roots of given quadratic equation are 25 and –1.
(10) 25m² = 9
Solution:
25m² = 9
25m² – 9 = 0
(5m)² – (3)² = 0
(5m + 3)(5m – 3) = 0 …[(a + b)(a – b) = a² – b²]
5m = – 3 or 5m = 3
m = – \(\large \frac {3}{5}\) or m = \(\large \frac {3}{5}\)
Ans: The roots of the given quadratic equation are \(\large \frac {3}{5}\) and − \(\large \frac {3}{5}\).
(11) 7m² = 21m
Solution:
7m² = 21m
7m² – 21m = 0
7m(m – 3) = 0
7m = 0 or m – 3 = 0
m = \(\large \frac {0}{7}\) or m = 3
m = 0 or m = 3
Ans: The roots of the given quadratic equation are 0 and 3.
(12) m² – 11 = 0
Solution:
m² – 11 = 0
m² – (\(\sqrt{11}\))² = 0
(m + 11)(m – 11) = 0 …[(a + b)(a – b) = a² – b²]
m + \(\sqrt{11}\) = 0 or m – \(\sqrt{11}\) = 0
m = – \(\sqrt{11}\) or m = \(\sqrt{11}\)
Ans: The roots of the given quadratic equation are – \(\sqrt{11}\) and \(\sqrt{11}\).
Practice set 2.3
Solve the following quadratic equations by completing the square method.
(1) x² + x – 20 = 0
Solution:
x² + x – 20 = 0
Term to be added:
= \(\large (\frac {1}{2}\) × coefficient of x\(\large)\)²
= \(\large (\frac {1}{2}\) × 1 \(\large)\)²
= \(\large (\frac {1}{2})\)²
= \(\large \frac {1}{4}\)
∴ x² + x + \(\large \frac {1}{4}\) – \(\large \frac {1}{4}\) – 20 = 0
∴ x² + x + \(\large \frac {1}{4}\) – \(\large \frac {1}{4}\) – 20 = 0
∴ \(\large(\)x + \(\large \frac {1}{2})\)² = \(\large \frac {1}{4}\) + 20
∴ \(\large(\)x + \(\large \frac {1}{2})\)² = \(\large \frac {1\,+\,80}{4}\)
∴ \(\large(\)x + \(\large \frac {1}{2})\)² = \(\large \frac {81}{4}\)
By taking square root, we get,
∴ x + \(\large \frac {1}{2}\) = ± \(\large \frac {9}{2}\)
∴ x + \(\large \frac {1}{2}\) = \(\large \frac {9}{2}\)
∴ x = \(\large \frac {9}{2}\) – \(\large \frac {1}{2}\)
∴ x = \(\large \frac {9\,–\,1}{2}\)
∴ x = \(\large \frac {8}{2}\)
∴ x = 4
∴ x + \(\large \frac {1}{2}\) = – \(\large \frac {9}{2}\)
∴ x = – \(\large \frac {9}{2}\) – \(\large \frac {1}{2}\)
∴ x = \(\large \frac {–\,9\,–\,1}{2}\)
∴ x = \(\large \frac {–\,10}{2}\)
∴ x = – 5
Ans: The roots of given quadratic equation are 4 and – 5.
(2) x² + 2x – 5 = 0
Solution:
x² + 2x – 5 = 0
Term to be added:
= \(\large (\frac {1}{2}\) × coefficient of x\(\large)\)²
= \(\large (\frac {1}{2}\) × 2 \(\large)\)²
= 1²
= 1
∴ x² + 2x + 1 – 1 – 5 = 0
∴ (x + 1)² = 1 + 5
∴ (x + 1)² = 6
By taking square root, we get,
∴ x + 1 = ± \(\sqrt{6}\)
∴ x + 1 = \(\sqrt{6}\)
∴ x = – 1 + \(\sqrt{6}\)
∴ x + 1 = – \(\sqrt{6}\)
∴ x = – 1 – \(\sqrt{6}\)
Ans: The roots of the given quadratic equation are – 1 + \(\sqrt{6}\) and – 1 – \(\sqrt{6}\)
(3) m² – 5m = – 3
Solution:
m² – 5m = – 3
m² – 5m + 3 = 0
Term to be added:
= \(\large (\frac {1}{2}\) × coefficient of m\(\large)\)²
= \(\large (\frac {1}{2}\) × (– 5) \(\large)\)²
= \(\large (\frac {-\,5}{2})\)²
= \(\large \frac {25}{4}\)
∴ m² – 5m + \(\large \frac {25}{4}\) – \(\large \frac {25}{4}\) + 3 = 0
∴ \((\large\)m – \(\large \frac {5}{2})\)² = \(\large \frac {25}{4}\) – 3
∴ \((\large\)m – \(\large \frac {5}{2})\)² = \(\large \frac {25\,-\,12}{4}\)
∴ \((\large\)m – \(\large \frac {5}{2})\)² = \(\large \frac {13}{4}\)
By taking square root, we get,
∴ m – \(\large \frac {5}{2}\) = ± \(\sqrt{\frac {13}{4}}\)
∴ m – \(\large \frac {5}{2}\) = \(\sqrt{\frac {13}{4}}\)
∴ m = \(\sqrt{\frac {13}{4}}\) + \(\large \frac {5}{2}\)
∴ m = \(\sqrt{\frac {13}{4}}\) + \(\large \frac {10}{4}\)
∴ m = \(\large \frac {\sqrt{13}\,+\,\large 10}{4}\)
∴ m – \(\large \frac {5}{2}\) = – \(\sqrt{\frac {13}{4}}\)
∴ m = – \(\sqrt{\frac {13}{4}}\) + \(\large \frac {5}{2}\)
∴ m = – \(\sqrt{\frac {13}{4}}\) + \(\large \frac {10}{4}\)
∴ m = \(\large \frac {-\sqrt{13}\,+\,\large 10}{4}\)
Ans: The roots of the given quadratic equation are \(\large \frac { \sqrt{13}\,+\,\large 10}{4}\) and \(\large \frac { -\sqrt{13}\,+\,\large 10}{4}\).
(4) 9y² – 12y + 2 = 0
Solution:
9y² – 12y + 2 = 0
Dividing both sides by 9, we get
y² – \(\large \frac {12}{9}\)y + \(\large \frac {2}{9}\) = 0
y² – \(\large \frac {4}{3}\)y + \(\large \frac {2}{9}\) = 0
Term to be added:
= \(\large (\frac {1}{2}\) × coefficient of y\(\large)\)²
= \(\large (\frac {1}{2}\) × \(\large \frac {4}{3}\) \(\large)\)²
= \(\large (\frac {-\,2}{3})\)²
= \(\large \frac {4}{9}\)
∴ y² – \(\large \frac {4}{3}\)y + \(\large \frac {4}{9}\) – \(\large \frac {4}{9}\) + \(\large \frac {2}{9}\) = 0
∴ \((\large\)y – \(\large \frac {2}{3})\)² = \(\large \frac {4}{9}\) – \(\large \frac {2}{9}\)
∴ \((\large\)y – \(\large \frac {2}{3})\)² = \(\large \frac {4\,-\,2}{9}\)
∴ \((\large\)y – \(\large \frac {2}{3})\)² = \(\large \frac {2}{9}\)
By taking square root, we get,
∴ y – \(\large \frac {2}{3}\) = ± \(\large \frac {\sqrt{2}}{3}\)
∴ y – \(\large \frac {2}{3}\) = \(\large \frac {\sqrt{2}}{3}\)
∴ y = \(\large \frac {\sqrt{2}}{3}\) + \(\large \frac {2}{3}\)
∴ y = \(\large \frac {\sqrt{2}\,+\,2}{3}\)
∴ y = \(\large \frac {2\,+\,\sqrt{2}}{3}\)
∴ y – \(\large \frac {2}{3}\) = – \(\large \frac {\sqrt{2}}{3}\)
∴ y = – \(\large \frac {\sqrt{2}}{3}\) + \(\large \frac {2}{3}\)
∴ y = \(\large \frac {-\,\sqrt{2}\,+\,2}{3}\)
∴ y = \(\large \frac {2\,-\,\sqrt{2}}{3}\)
Ans: The roots of given quadratic equation are \(\large \frac {2\,+\,\sqrt{2}}{3}\) and \(\large \frac {2\,-\,\sqrt{2}}{3}\).
(5) 2y² + 9y + 10 = 0
Solution:
2y² + 9y + 10 = 0
Dividing both sides by 2, we get
y² + \(\large \frac {9}{2}\)y + 5 = 0
Term to be added:
= \(\large (\frac {1}{2}\) × coefficient of y\(\large)\)²
= \(\large (\frac {1}{2}\) × \(\large \frac {-\,9}{2}\) \(\large)\)²
= \(\large (\frac {-\,9}{4})\)²
= \(\large \frac {81}{16}\)
∴ y² + \(\large \frac {9}{2}\)y + \(\large \frac {81}{16}\) – \(\large \frac {81}{16}\) + 5 = 0
∴ \((\large\)y + \(\large \frac {9}{4})\)² = \(\large \frac {81}{16}\) – 5
∴ \((\large\)y + \(\large \frac {9}{4})\)² = \(\large \frac {81\,-\,80}{16}\)
∴ \((\large\)y + \(\large \frac {9}{4})\)² = \(\large \frac {1}{16}\)
By taking square root, we get,
∴ y + \(\large \frac {9}{4}\) = ± \(\large \frac {1}{4}\)
∴ y + \(\large \frac {9}{4}\) = \(\large \frac {1}{4}\)
∴ y = \(\large \frac {1}{4}\) – \(\large \frac {9}{4}\)
∴ y = \(\large \frac {1\,-\,9}{4}\)
∴ y = \(\large \frac {-\,8}{4}\)
∴ y = – 2
∴ y + \(\large \frac {9}{4}\) = – \(\large \frac {1}{4}\)
∴ y = – \(\large \frac {1}{4}\) – \(\large \frac {9}{4}\)
∴ y = \(\large \frac {-\,1\,-\,9}{4}\)
∴ y = \(\large \frac {-\,10}{4}\)
∴ y = \(\large \frac {-\,5}{2}\)
Ans: The roots of the given quadratic equation are – 2 and \(\large \frac {-\,5}{2}\).
(6) 5x² = 4x + 7
Solution:
5x² = 4x + 7
5x² – 4x – 7 = 0
Dividing both sides by 5, we get
x² – \(\large \frac {4}{5}\) x – \(\large \frac {7}{5}\) = 0
Term to be added:
= \(\large (\frac {1}{2}\) × coefficient of x\(\large)\)²
= \(\large (\frac {1}{2}\) × \(\large \frac {-\,4}{5}\) \(\large)\)²
= \(\large (\frac {-\,2}{5})\)²
= \(\large \frac {4}{25}\)
∴ x² – 4x + \(\large \frac {4}{25}\) – \(\large \frac {4}{25}\) – \(\large \frac {7}{5}\) = 0
∴ \((\large\)x + \(\large \frac {1}{2})\)² = \(\large \frac {4}{25}\) + \(\large \frac {7}{5}\)
∴ \((\large\)x – \(\large \frac {2}{5})\)² = \(\large \frac {4\,+\,35}{25}\)
∴ \((\large\)x – \(\large \frac {2}{5})\)² = \(\large \frac {39}{25}\)
By taking square root, we get,
∴ x – \(\large \frac {2}{5}\) = ± \(\large \frac {\sqrt{39}}{5}\)
∴ x – \(\large \frac {2}{5}\) = \(\large \frac {\sqrt{39}}{5}\)
∴ x = \(\large \frac {\sqrt{39}}{5}\) + \(\large \frac {2}{5}\)
∴ x = \(\large \frac {\sqrt{39}\,+\,2}{5}\)
∴ x = \(\large \frac {2\,+\,\sqrt{39}}{5}\)
∴ x – \(\large \frac {2}{5}\) = – \(\large \frac {\sqrt{39}}{5}\)
∴ x = – \(\large \frac {\sqrt{39}}{5}\) + \(\large \frac {2}{5}\)
∴ x = \(\large \frac {-\,\sqrt{39}\,+\,2}{5}\)
∴ x = \(\large \frac {2\,-\,\sqrt{39}}{5}\)
Ans: The roots of the given quadratic equation are \(\large \frac {2\,+\,\sqrt{39}}{5}\) and \(\large \frac {2\,-\,\sqrt{39}}{5}\).
Practice set 2.4
1. Compare the given quadratic equations to the general form and write values of a, b, c.
(1) x² – 7x + 5 = 0
Solution:
x² – 7x + 5 = 0
Comparing with ax² + bx + c = 0, we get,
a = 1, b = –7, c = 5
(2) 2m² = 5m – 5
Solution:
2m² = 5m – 5
∴ 2m² – 5m + 5 = 0
Comparing with am² + bm + c = 0, we get,
a = 2, b = – 5, c = 5
(3) y² = 7y
Solution:
y² = 7y
y² – 7y = 0
y² – 7y + 0 = 0
Comparing with ay² + by + c = 0, we get,
a = 1, b = –7, c = 0
2. Solve using formula.
(1) x² + 6x + 5 = 0
Solution:
x² + 6x + 5 = 0
Comparing with ax² + bx + c = 0, we get,
a = 1, b = 6, c = 5
∴ b² – 4ac = (6)² – 4 × 1 × 5
∴ b² – 4ac = 36 – 20
∴ b² – 4ac = 16
∴ x = \(\large \frac {-\,b\,±\,\sqrt{b²\,-\,4ac}}{2a}\)
∴ x = \(\large \frac {-\,6\,±\,\sqrt{16}}{2(1)}\)
∴ x = \(\large \frac {-\,6\,±\,4}{2}\)
∴ x = \(\large \frac {-\,6\,+\,4}{2}\)
∴ x = \(\large \frac {-\,2}{2}\)
∴ x = – 1
∴ x = \(\large \frac {-\,6\,–\,4}{2}\)
∴ x = \(\large \frac {-\,10}{2}\)
∴ x = – 5
Ans: The roots of the given quadratic equation are –1 and –5.
(2) x² – 3x – 2 = 0
Solution:
x² – 3x – 2 = 0
Comparing with ax² + bx + c = 0, we get,
a = 1, b = – 3, c = – 2
∴ b² – 4ac = (– 3)² – 4 × 1 × (– 2)
∴ b² – 4ac = 9 + 8
∴ b² – 4ac = 17
∴ x = \(\large \frac {-\,b\,±\,\sqrt{b²\,-\,4ac}}{2a}\)
∴ x = \(\large \frac {-\,(-\,3)\,±\,\sqrt{17}}{2(1)}\)
∴ x = \(\large \frac {3\,±\,\sqrt{17}}{2}\)
∴ x = \(\large \frac {3\,+\,\sqrt{17}}{2}\)
∴ x = \(\large \frac {3\,-\,\sqrt{17}}{2}\)
Ans: The roots of the given quadratic equation are \(\large \frac {3\,+\,\sqrt{17}}{2}\) and \(\large \frac {3\,-\,\sqrt{17}}{2}\).
(3) 3m² + 2m – 7 = 0
Solution:
3m² + 2m – 7 = 0
Comparing with am² + bm + c = 0, we get,
a = 3, b = 2, c = – 7
∴ b² – 4ac = (2)² – 4 × 3 × (– 7)
∴ b² – 4ac = 4 + 84
∴ b² – 4ac = 88
∴ m = \(\large \frac {-\,b\,±\,\sqrt{b²\,-\,4ac}}{2a}\)
∴ m = \(\large \frac {-\,2\,±\,\sqrt{88}}{2(3)}\)
∴ m = \(\large \frac {-\,2\,±\,2\sqrt{22}}{6}\)
∴ m = \(\large \frac {2(-\,1\,±\,\sqrt{22}}{6}\)
∴ m = \(\large \frac {-\,1\,±\,\sqrt{22}}{3}\)
∴ m = \(\large \frac {-\,1\,+\,\sqrt{22}}{3}\)
∴ m = \(\large \frac {-\,1\,-\,\sqrt{22}}{3}\)
Ans: The roots of given quadratic equation are \(\large \frac {-\,1\,+\,\sqrt{22}}{3}\) and \(\large \frac {-\,1\,-\,\sqrt{22}}{3}\).
(4) 5m² – 4m – 2 = 0
Solution:
5m² – 4m – 2 = 0
Comparing with am² + bm + c = 0, we get,
a = 5, b = – 4, c = – 2.
∴ b² – 4ac = (– 4)² – 4 × 5 × (– 2)
∴ b² – 4ac = 16 + 40
∴ b² – 4ac = 56
∴ m = \(\large \frac {-\,b\,±\,\sqrt{b²\,-\,4ac}}{2a}\)
∴ m = \(\large \frac {-\,(-\,4)\,±\,\sqrt{56}}{2(5)}\)
∴ m = \(\large \frac {4\,±\,2\sqrt{14}}{10}\)
∴ m = \(\large \frac {2(2\,±\,\sqrt{14})}{10})\)
∴ m = \(\large \frac {2\,±\,\sqrt{14}}{10}\)
∴ m = \(\large \frac {2\,+\,\sqrt{14}}{10}\)
∴ m = \(\large \frac {2\,-\,\sqrt{14}}{10}\)
Ans: The roots of given quadratic equation are \(\large \frac {2\,+\,\sqrt{14}}{10}\) and \(\large \frac {2\,-\,\sqrt{14}}{10}\).
(5) y² + \(\large \frac {1}{3}\)y = 2
Solution:
y² + \(\large \frac {1}{3}\)y = 2
∴ y² + \(\large \frac {1}{3}\)y – 2 = 0
Multiplying both sides by 3, we get,
∴ 3y² + y – 6 = 0
Comparing with ay² + by + c = 0 we get,
a = 3, b = 1, c = – 6.
∴ b² – 4ac = (1)² – 4 × 3 × (– 6)
∴ b² – 4ac = 1 + 72
∴ b² – 4ac = 73
∴ y = \(\large \frac {-\,b\,±\,\sqrt{b²\,-\,4ac}}{2a}\)
∴ y = \(\large \frac {-\,1\,±\,\sqrt{73}}{2(3)}\)
∴ y = \(\large \frac {-\,1\,±\,\sqrt{17}}{6}\)
∴ y = \(\large \frac {-\,1\,+\,\sqrt{17}}{6}\)
∴ y = \(\large \frac {-\,1\,-\,\sqrt{17}}{6}\)
Ans: The roots of given quadratic equation are \(\large \frac {-\,1\,+\,\sqrt{17}}{6}\) and \(\large \frac {-\,1\,-\,\sqrt{17}}{6}\).
(6) 5x² + 13x + 8 = 0
Solution:
5x² + 13x + 8 = 0
Comparing with ax² + bx + c = 0 we get,
a = 5, b = 13, c = 8.
∴ b² – 4ac = (13)² – 4 × 5 × 13
∴ b² – 4ac = 169 + 160
∴ b² – 4ac = 9
∴ x = \(\large \frac {-\,b\,±\,\sqrt{b²\,-\,4ac}}{2a}\)
∴ x = \(\large \frac {-\,13\,±\,\sqrt{9}}{2(5)}\)
∴ x = \(\large \frac {-\,13\,±\,3}{10}\)
∴ x = \(\large \frac {-\,13\,+\,3}{10}\)
∴ x = \(\large \frac {-\,10}{10}\)
∴ x = – 1
∴ x = \(\large \frac {-\,13\,-\,3}{10}\)
∴ x = \(\large \frac {-\,16}{10}\)
∴ x = \(\large \frac {-\,8}{5}\)
Ans: The roots of the given quadratic equation are – 1 and \(\large \frac {-\,8}{5}\).
(3) With the help of the flow chart given below, solve the equation x² + 2 \(\sqrt{3}\)x + 3 = 0 using the formula.
Solution :

x² + 2 \(\sqrt{3}\)x + 3 = 0
Comparing with ax² + bx + c = 0, we get,
a = 1, b = 2 \(\sqrt{3}\), c = 3
∴ b² – 4ac = (2 \(\sqrt{3}\))² – 4 × 1 × 3
∴ b² – 4ac = 12 – 12
∴ b² – 4ac = 0
∴ x = \(\large \frac {-\,b\,±\,\sqrt{b²\,-\,4ac}}{2a}\)
∴ x = \(\large \frac {-\,2 \sqrt{3}\,±\,\sqrt{0}}{2(1)}\)
∴ x = \(\large \frac {-\,2 \sqrt{3}}{2}\)
∴ x = – \(\sqrt{3}\)
Ans: The root of given quadratic equation is – \(\sqrt{3}\)
Practice set 2.5
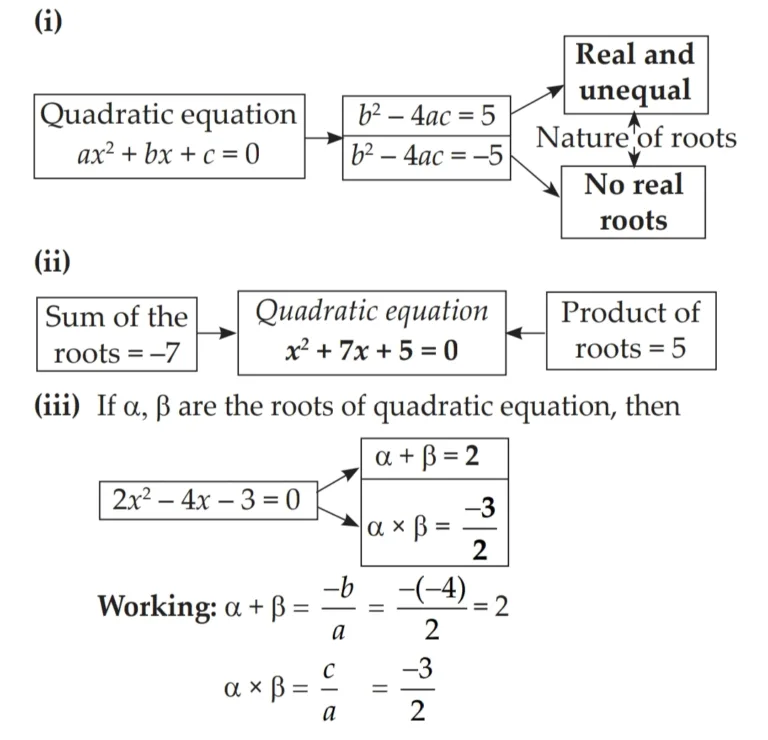
1. Activity : Fill in the gaps and complete.
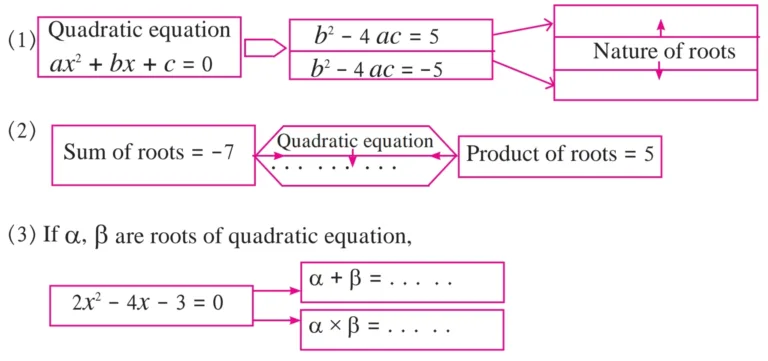
Solution:
2. Find the value of discriminant.
(1) x² + 7x – 1 = 0
Solution:
x² + 7x – 1 = 0
Comparing with ax² + bx + c = 0, we get
a = 1, b = 7, c = – 1
∆ = b² – 4ac
∴ ∆ = (7)² – 4 × 1 × (– 1)
∴ ∆ = 49 + 4
∴ ∆ = 53
Ans: The value of the discriminant is 53.
(2) 2y² – 5y + 10 = 0
Solution:
2x² – 5y + 10 = 0
Comparing with ay² + by + c = 0, we get
a = 2, b = – 5, c = 10
∆ = b² – 4ac
∴ ∆ = (– 5)² – 4 × 2 × 10
∴ ∆ = 25 – 80
∴ ∆ = – 55
Ans: The value of the discriminant is – 55.
(3) \(\sqrt{2}\) x² + 4x + 2 \(\sqrt{2}\) = 0
Solution:
\(\sqrt{2}\) x² + 4x + 2 \(\sqrt{2}\) = 0
Comparing with ax² + bx + c = 0, we get
a = \(\sqrt{2}\), b = 4, c = 2 \(\sqrt{2}\)
∆ = b² – 4ac
∴ ∆ = (4)² – 4 × \(\sqrt{2}\) × 2 \(\sqrt{2}\)
∴ ∆ = 16 – 16
∴ ∆ = 0
Ans: The value of the discriminant is 0.
3. Determine the nature of roots of the following quadratic equations.
(1) x² – 4x + 4 = 0
Solution:
x² – 4x + 4 = 0
Comparing with ax² + bx + c = 0 we get,
a = 1, b = – 4, c = 4
∆ = b² – 4ac
∴ ∆ = (– 4)² – 4 × 1 × 4
∴ ∆ = 16 – 16
∴ ∆ = 0
∵ ∆ = 0
∴ The roots of the quadratic equation are real and equal.
(2) 2y² – 7y + 2 = 0
Solution:
2y² – 7y + 2 = 0
Comparing with ay² + by + c = 0 we get,
a = 2, b = –7, c = 2
∆ = b² – 4ac
∴ ∆ = (– 7)² – 4 × 2 × 2
∴ ∆ = 49 – 16
∴ ∆ = 33
∵ ∆ > 0
∴ The roots of the quadratic equation are real and unequal.
(3) m² + 2m + 9 = 0
Solution:
m² + 2m + 9 = 0
Comparing with am² + bm + c = 0 we get,
a = 1, b = 2, c = 9
∆ = b² – 4ac
∴ ∆ = (2)2 – 4 × 1 × 9
∴ ∆ = 4 – 36
∴ ∆ = – 32
∵ ∆ < 0
∴ The roots of the quadratic equation are not real.
4. Form the quadratic equation from the roots given below.
(1) 0 and 4
Solution:
Let α and β are the roots of the quadratic equation
∴ α = 0 and β = 4
Now,
α + β = 0 + 4
∴ α + β = 4
α × β = 0 × 4
∴ α × β = 0
Then,
The quadratic equation is,
x² – (α + β)x + αβ = 0
x² – 4x + 0 = 0
x² – 4x = 0
Ans: The quadratic equation is x² – 4x = 0
(2) 3 and – 10
Solution:
Let α and β are the roots of the quadratic equation
∴ α = 3 and β = – 10
Now,
α + β = 3 + (– 10)
∴ α + β = 3 – 10
∴ α + β = – 7
α × β = 3 × (– 10)
∴ α × β = – 30
Then,
The quadratic equation is,
x² – (α + β)x + αβ = 0
x² – (– 7)x + (– 30) = 0
x² + 7x – 30 = 0
Ans: The quadratic equation is x² + 4x – 30 = 0
(3) \(\large \frac {1}{2}\), \(\large \frac {-\,1}{2}\)
Solution:
Let α and β are the roots of the quadratic equation
∴ α = \(\large \frac {1}{2}\) and β = – \(\large \frac {1}{2}\)
Now,
α + β = \(\large \frac {1}{2}\) + (– \(\large \frac {1}{2}\))
∴ α + β = \(\large \frac {1}{2}\) – \(\large \frac {1}{2}\)
∴ α + β = 0
α × β = \(\large \frac {1}{2}\) × (– \(\large \frac {1}{2}\))
∴ α × β = – \(\large \frac {1}{4}\)
Then,
The quadratic equation is,
x² – (α + β)x + αβ = 0
x² – (0)x + \(\large (– \,\frac {1}{4})\) = 0
x² – \(\large (\frac {1}{4})\) = 0
Multiplying by 4 on both sides, we get,
4x² – 1 = 0
Ans: The quadratic equation is 4x² – 1 = 0
(4) 2 – \(\sqrt{5}\) , 2 + \(\sqrt{5}\)
Solution:
Let α and β are the roots of the quadratic equation
∴ α = 2 – \(\sqrt{5}\) and β = 2 + \(\sqrt{5}\)
Now,
α + β = 2 – \(\sqrt{5}\) + 2 + \(\sqrt{5}\)
∴ α + β = 2 + 2
∴ α + β = 4
α × β = (2 – \(\sqrt{5}\)) × (2 + \(\sqrt{5}\))
∴ α × β = 2² – \((\sqrt{5})\)²
∴ α × β = 4 – 5
∴ α × β = – 1
Then,
The quadratic equation is,
x² – (α + β)x + αβ = 0
x² – (4)x + (– 1) = 0
x² – 4x – 1 = 0
Ans: The quadratic equation is x² – 4x – 1 = 0.
5. Sum of the roots of a quadratic equation is double their product. Find k if equation is x² – 4kx + k + 3 = 0
Solution:
Let α and β are the roots of the given quadratic equation
x² – 4kx + k + 3 = 0
Comparing with ax² + bx + c = 0 we get,
a = 1, b = – 4k, c = k + 3
α + β = \(\large \frac {-\,b}{a}\)
∴ α + β = \(\large \frac {-\,(-\,4k)}{1}\)
∴ α + β = 4k
α × β = \(\large \frac {c}{a}\)
∴ α × β = \(\large \frac {k\,+\,3}{1}\)
∴ α × β = k + 3
Now,
α + β = 2 (α × β) …[Given]
∴ 4k = 2 (k + 3)
∴ 4k = 2k + 6
∴ 4k – 2k = 6
∴ 2k = 6
∴ k = \(\large \frac {6}{2}\)
∴ k = 3
Ans: The value of k is 3.
6. α, β are roots of y² – 2y – 7 = 0 find,
(1) α² + β²
(2) a³ + b³
Solution:
y² – 2y – 7 = 0
Comparing with ay² + by + c = 0 we get,
a = 1, b = – 2, c = – 7
α + β = \(\large \frac {-\,b}{a}\)
∴ α + β = \(\large \frac {-\,2}{1}\)
∴ α + β = 2
α × β = \(\large \frac {c}{a}\)
∴ α × β = \(\large \frac {-\,7}{1}\)
∴ α × β = − 7
(i) α² + β² = (α + β)² – 2αβ
∴ α² + β² = (2)² – 2 × (– 7)
∴ α² + β² = 4 + 14
∴ α² + β² = 18
(ii) α³ + β³ = (α + β)³ – 3αβ (α + β)
∴ α³ + β³= (2)³ – 3 × (– 7) × (2)
∴ α³ + β³ = 8 + 42
∴ α³ + β³ = 50
Ans: The value of α² + β² is 18 and α³ + β³ is 50
7. The roots of each of the following quadratic equations are real and equal, find k.
(1) 3y² + ky + 12 = 0
Solution:
3y² + ky + 12 = 0
Comparing the above equation with ay² + by + c = 0, we get,
a = 3, b = k, c = 12
∆ = b² – 4ac
∴ ∆ = (k)² – 4 × 3 × 12
∴ ∆ = k² – 144
The roots are real and equal, so ∆ must be zero.
∴ k² – 144 = 0
∴ k² = 144
∴ k = ± 12
k = 12 or k = – 12
Ans: The value of k is 12 or – 12.
(2) kx (x – 2) + 6 = 0
Solution:
kx(x – 2) + 6 = 0
kx² – 2kx + 6 = 0
Comparing with ax² + bx + c = 0, we get,
a = k, b = – 2k, c = 6
∆ = b² – 4ac
∴ ∆ = (– 2k)²– 4 × k × 6
∴ ∆ = 4k² – 24k
The roots are real and equal, so ∆ must be zero.
∴ 4k² – 24k = 0
∴ 4k(k – 6) = 0
∴ 4k = 0 or k – 6 = 0
∴ k = \(\large \frac {0}{4}\) or k = 6
∴ k = 0 or k = 6.
As a = k and in quadratic equation a ≠ 0
∴ k ≠ 0
∴ k = 6
Ans: The value of k is 6.
Practice set 2.6
1. Product of Pragati’s age 2 years ago and 3 years hence is 84. Find her present age.
Solution:
Let the present age of Pragati be x years.
Pragati’s age 2 years ago = (x – 2) years and 3 years hence = (x + 3) years.
According to given condition,
(x – 2) (x + 3) = 84
x(x + 3) – 2(x + 3) = 84
x² + 3x – 2x – 6 = 84
x² + x – 6 – 84 = 0
x² + x – 90 = 0
x² + 10x – 9x – 90 = 0
x(x + 10) – 9(x + 10) = 0
(x + 10) (x – 9) = 0
x + 10 = 0 or x – 9 = 0
x = – 10 or x = 9
Now, x ≠ 10 as age cannot be negative.
∴ x = 9
Ans: The present age of Pragati is 9 years.
2. Sum of squares of 2 consecutive natural even numbers is 244; find the numbers.
Solution:
Let the two consecutive even natural numbers be x and x + 2 years.
According to given condition,
x² + (x + 2)² = 244
x² + x² + 4x + 4 = 244 …[∵ (a + b)² = a² + 2ab + b²]
2x² + 4x + 4 – 244 = 0
2x² + 4x – 240 = 0
x² + 2x – 120 = 0 …[Dividing both sides by 2]
x² + 12x – 10x – 120 = 0
x(x + 12) – 10(x + 12) = 0
(x + 12) (x – 10) = 0
x + 12 = 0 or x – 10 = 0
x = –12 or x = 10
Now, x ≠ –12 as natural numbers cannot be negative.
x = 10
and x + 2 = 10 + 2 = 12
Ans: The two numbers are 10 and 12.
3. In the orange garden of Mr. Madhusudan there are 150 orange trees. The number of trees in each row is 5 more than that in each column. Find the number of trees in each row and each column with the help of the following flow chart.
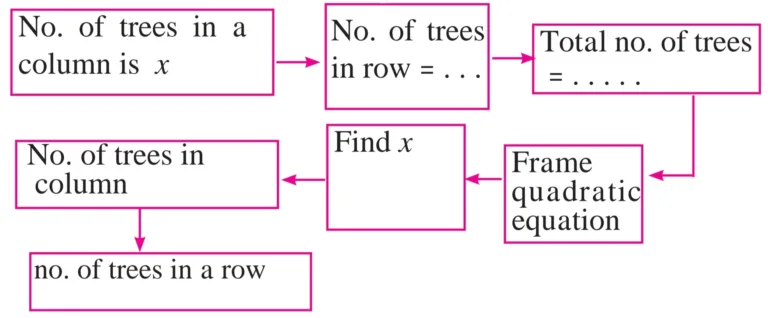
Solution:
Let the number of trees planted in vertical rows be x.
The number of trees planted in horizontal rows is (x + 5).
∴ The total number of trees planted = x × (x + 5)
But, the total number of trees planted is 150.
∴ x × (x + 5) = 150
∴ x² + 5x = 150
∴ x² + 5x – 150 = 0
∴ x² + 15x – 10x – 150 = 0
∴ x(x + 15) – 10(x + 15) = 0
∴ (x + 15) (x – 10) = 0
∴ x + 15 = 0 or x – 10 = 0
∴ x = –15 or x = 10
Now, x ≠ –15 as the number of trees cannot be negative.
∴ x = 10 and x + 5 = 10 + 5 = 15
Ans: The number of trees planted in horizontal rows is 15 and 10 trees planted in vertical rows.
4. Vivek is older than Kishor by 5 years. The sum of the reciprocals of their ages is \(\large \frac {1}{6}\). Find their present ages.
Solution:
Let the present age of Kishor be x years.
∴ The present age of Vivek is (x + 5) years.
According to given condition,
\(\large \frac {1}{x}\) + \(\large \frac {1}{x\,+\,5}\) = \(\large \frac {1}{6}\)
\(\large \frac {x\,+\,5\,+\,x}{x(x\,+\,5)}\) = \(\large \frac {1}{6}\)
\(\large \frac {2x\,+\,5}{x²\,+\,5x}\) = \(\large \frac {1}{6}\)
x² + 5x = 12x + 30
x² + 5x – 12x – 30 = 0
x² – 7x – 30 = 0
x² – 10x + 3x – 30 = 0
x(x – 10) + 3(x – 10) = 0
(x – 10) (x + 3) = 0
x – 10 = 0 or x + 3 = 0
x = 10 or x = –3
Now, x ≠ – 3 as age cannot be negative.
∴ x = 10 and x + 5 = 10 + 5 = 15
Ans: The present age of Kishor is 10 years and present age of Vivek is 15 years.
5. Suyash scored 10 marks more in the second test than that in the first. 5 times the score of the second test is the same as the square of the score in the first test. Find his score in the first test.
Solution:
Let the marks scored by Suyash in first unit test be x.
The marks scored by him in second unit test is (x + 10)
According to given condition,
5 × (x + 10) = x2
5x + 50 = x²
x² – 5x – 50 = 0
x² – 10x + 5x – 50 = 0
x(x – 10) + 5(x – 10) = 0
(x – 10) (x + 5) = 0
x – 10 = 0 or x + 5 = 0
x = 10 or x = –5
Now, x ≠ – 5 as marks scored in the unit test cannot be negative.
∴ x = 10
Ans: The marks scored by Suyash in the first test is 10.
6. Mr. Kasam runs a small business of making earthen pots. He makes a certain number of pots on a daily basis. Production cost of each pot is ₹ 40 more than 10 times total number of pots, he makes in one day. If production cost of all pots per day is ₹ 600, find production cost of one pot and number of pots he makes per day.
Solution:
Let the number of pots made by Mr Kasam in each day be x.
The cost price of each pot = ₹ (10x + 40)
Total cost price of all pots made by him in one day = ₹ 600
According to given condition,
x × (10x + 40) = 600
10x² + 40x = 600
10x² + 40x – 600 = 0
x² + 4x – 60 = 0 …[Dividing both sides by 10]
x² + 10x – 6x – 60 = 0
x(x + 10) – 6(x + 10) = 0
(x + 10) (x – 6) = 0
x + 10 = 0 or x – 6 = 0
x = –10 or x = 6
Now, x ≠ –10 as the number of pots cannot be negative.
∴ x = 6
and 10x + 40 = 10 × 6 + 40
∴ 10x + 40 = 60 + 40
∴ 10x + 40 = 100
Ans: Mr. Kasam makes 6 pots everyday and the cost of each pot is ₹ 100.
7. Pratik takes 8 hours to travel 36 km downstream and return to the same spot. The speed of the boat in still water is 12 km. per hour. Find the speed of water current.
Solution:
Let the speed of the river current be x km/h.
The speed of the boat in still water is 12 km/hr.
∴ The speed of the boat in downstream is (12 + x) km/hr and the speed of boat in upstream is (12 – x) km/hr [x < 12]
Time = \(\large \frac {Distance}{Speed}\)
Time taken by boat to travel 36 km downstream = \(\large \frac {36}{12 \,+\,x}\) hours
Time taken by boat to travel 36 km upstream = \(\large \frac {36}{12 \,-\,x}\) hours
Total time taken to travel is 8 hours.
According to given condition,
\(\large \frac {36}{12 \,+\,x}\) + \(\large \frac {36}{12 \,-\,x}\) = 8
36 \(\large (\frac {1}{12 \,+\,x}\) + \(\large \frac {1}{12 \,-\,x})\) = 8
\(\large (\frac {12\,-\,x\,-\,12\,-\,x}{(12 \,+\,x)(12\,-\,x)})\) = \(\large \frac {8}{36}\)
\(\large \frac {24}{12²\,-\,x²}\) = \(\large \frac {2}{9}\) ….[Using (a + b)(a – b) = a² – b²]
\(\large \frac {12}{144\,-\,x²}\) = \(\large \frac {1}{9}\) …[Dividing by 2 on both sides]
12 × 9 = 144 – x²
108 = 144 – x²
x² = 144 – 108
x² = 36
x² – 36 = 0
(x + 6)(x – 6) = 0
x + 6 = 0 or x – 6 = 0
x = – 6 or x = 6
Now, x ≠ – 6 as speed of river current cannot be negative.
∴ x = 6
Ans: The speed of the river current is 6 km/hr.
8. Pintu takes 6 days more than those of Nishu to complete certain work. If they work together they finish it in 4 days. How many days would it take to complete the work if they work alone.
Solution:
Let Nishu take x days to complete the work.
∴ Pintu takes (x + 6) days to complete the work.
Work done by Nishu in 1 day = \(\large \frac {1}{x}\)
∴ Work done by Pintu in 1 day = \(\large \frac {1}{x \,+\, 6}\)
∴ Work done by both of them in 1 day = \(\large \frac {1}{x}\) + \(\large \frac {1}{x \,+\, 6}\)
But, together they complete the work in 4 days.
∴ Work done by both of them in 1 day = \(\large \frac {1}{4}\)
According to given condition,
\(\large \frac {1}{x}\) + \(\large \frac {1}{x \,+\, 6}\) = \(\large \frac {1}{4}\)
∴ \(\large \frac {x\,+\,6\,+\,x}{x(x \,+\, 6)}\) = \(\large \frac {1}{4}\)
∴ \(\large \frac {2x\,+\,6}{x² \,+\, 6x}\) = \(\large \frac {1}{4}\)
∴ x² + 6x = 8(2x + 6)
∴ x² + 6x = 8x + 24
∴ x² + 6x – 8x – 24 = 0
∴ x² – 2x – 24 = 0
∴ x² – 6x + 4x – 24 = 0
∴ x(x – 6) + 4(x – 6) = 0
∴ (x – 6) (x + 4) = 0
∴ x – 6 = 0 or x + 4 = 0
∴ x = 6 or x = – 4
Now, x ≠ – 4 as the number of days cannot be negative.
∴ x = 6
and x + 6 = 6 + 6 = 12
Ans: Nishu takes 6 days and Pintu takes 12 days to complete the work.
9. If 460 is divided by a natural number, the quotient is 6 more than five times the divisor and remainder is 1. Find quotient and divisor.
Solution:
Let the divisor be x
Dividend = 460
Remainder = 1
According to the given condition,
Quotient = 5x + 6
We know that,
Dividend = Divisor × Quotient + Remainder
∴ 460 = x × (5x + 6) + 1
∴ 460 = 5x² + 6x + 1
∴ 5x² + 6x +1 – 460 = 0
∴ 5x² + 6x – 459 = 0
∴ 5x² – 45x + 51x – 459 = 0
∴ 5x(x – 9) + 51(x – 9) = 0
∴ (x – 9) (5x + 51) = 0
∴ x – 9 = 0 or 5x + 51 = 0
∴ x = 9 or x = \(\large \frac {-\,51}{5}\)
x ≠ \(\large \frac {-\,51}{5}\) as natural numbers cannot be negative.
∴ x = 9
and 5x + 6 = 5 × 9 + 6 = 51.
Ans: The divisor is 9 and the quotient is 51.
10. In the above fig. □ ABCD is a trapezium AB II CD and its area is 33 cm². From the information given in the figure, find the lengths of all sides of the □ ABCD. Fill in the empty boxes to get the solution.
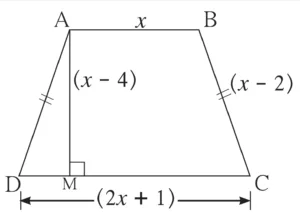
Solution:
□ ABCD is a trapezium
AB || CD
A (□ ABCD) = \(\large \frac {1}{2}\) (AB + CD) × □
33 = \(\large \frac {1}{2}\) (x + 2x + 1) × □
∴ □ = (3x + 1) × □
∴ 3x² + □ – □ = 0
∴ 3x (__) +10(__) = 0
∴ (3x +10)(__) = 0
∴ (3x +10) = 0 or □ = 0
∴ x = \(\large \frac {-\,10}{3}\) or x = □
But length is never negative.
∴ x ≠ \(\large \frac {-\,10}{3}\)
∴ x = □
AB = ___, CD = ___, AD = BC = ___
Solution:
□ ABCD is a trapezium
AB || CD
A (□ ABCD) = \(\large \frac {1}{2}\) (AB + CD) × AM
33 = \(\large \frac {1}{2}\) (x + 2x + 1) × (x – 4)
∴ 66 = (3x + 1) × (x – 4)
∴ 3x² + (– 11x) – 70 = 0
∴ 3x (x – 7) +10 (x – 7) = 0
∴ (3x +10) (x – 7) = 0
∴ (3x + 10) = 0 or (x – 7) = 0
∴ x = \(\large \frac {-\,10}{3}\) or x = 7
But length is never negative.
∴ x ≠ \(\large \frac {-\,10}{3}\)
∴ x = 7
∴ AB = 7 cm, CD = 15 cm, AD = BC = 5 cm
Problem Set 2
1. Choose the correct answers for the following questions.
(1) Which one is the quadratic equation ?
(A) \(\large \frac {5}{x}\) – 3 = x²
(B) x (x + 5) = 2
(C) n – 1 = 2n
(D) \(\large \frac {1}{x²}\)(x + 2) = x
Ans: Option (B) : x (x + 5) = 2
Solution:
x (x + 5) = 2
∴ x² + 5x = 2
∴ x² + 5x – 2 = 0
Here, x is the only variable and maximum index of variable x is 2.
∴ It is a quadratic equation in variable x.
(2) Out of the following equations which one is not a quadratic equation ?
(A) x² + 4x = 11 + x²
(B) x² = 4x
(C) 5x² = 90
(D) 2x – x² = x² + 5
Ans: Option (A) : x² + 4x = 11 + x²
Solution:
x² + 4x = 11 + x²
∴ x² – x² + 4x – 11 = 0
∴ 4x – 11 = 0
Here, x is the only variable but the maximum index of variable x is 1 and not 2.
∴ It is not a quadratic equation.
(3) The roots of x² + kx + k = 0 are real and equal, find k.
(A) 0
(B) 4
(C) 0 or 4
(D) 2
Ans: Option (C) : 0 or 4
Solution:
x² + kx + k = 0
Comparing with ax² + bx + c = 0, we get a = 1, b = k, c = k
Since the equation has equal roots
∴ ∆ = 0
∴ b² – 4ac = 0
∴ k² – 4(1)(k) = 0
∴ k² – 4k = 0
∴ (k – 4) = 0
∴ k = 0 or k – 4 = 0
∴ k = 0 or k = 4
(4) For \(\sqrt{2}\)x² – 5x + \(\sqrt{2}\) = 0 find the value of the discriminant.
(A) – 5
(B) 17
(C) \(\sqrt{2}\)
(D) 2\(\sqrt{2}\) – 5
Ans: Option (B) : 17
Solution:
\(\sqrt{2}\)x² – 5x + \(\sqrt{2}\) = 0
Comparing with ax² + bx + c = 0 we get,
a = 2 , b = – 5, c = 2
∆ = b² – 4ac
∴ ∆ = (– 5)² – 4(\(\sqrt{2}\))(\(\sqrt{2}\))
∴ ∆ = 25 – 8
∴ ∆ = 17
(5) Which of the following quadratic equations has roots 3, 5 ?
(A) x² – 15x + 8 = 0
(B) x² – 8x + 15 = 0
(C) x² + 3x + 5 = 0
(D) x² + 8x – 15 = 0
Ans: Option (B) : x² – 8x + 15 = 0
Solution:
Here, α = 3, β = 5
α + β = 3 + 5 = 8
αβ = 3 × 5 = 15
The required equation is,
x² – (α + β)x + αβ = 0
x² – 8x + 15 = 0
(6) Out of the following equations, find the equation having the sum of its roots – 5.
(A) 3x² – 15x + 3 = 0
(B) x² – 5x + 3 = 0
(C) x² + 3x – 5 = 0
(D) 3x² + 15x + 3 = 0
Ans: Option (D) : 3x² + 15x + 3 = 0
Solution:
Sum of the roots is – 5
For equation 3x² + 15x + 3 = 0
Comparing with ax² + bx + c = 0
a = 3, b = 15, c = 3
Product of roots = \(\large \frac {c}{a}\)
∴ Product of roots = \(\large \frac {-\,15}{3}\)
∴ Product of roots = – 5
(7) \(\sqrt{5}\)m² – \(\sqrt{5}\)m + \(\sqrt{5}\) = 0, which of the following statements is true for this given equation?
(A) Real and unequal roots
(B) Real and equal roots
(C) Roots are not real
(D) Three roots.
Ans: Option (C) : Roots are not real
Solution:
\(\sqrt{5}\)m² – \(\sqrt{5}\)m + \(\sqrt{5}\) = 0
Comparing with am² + bm + c = 0
a = \(\sqrt{5}\), b = – \(\sqrt{5}\), c = \(\sqrt{5}\)
b² – 4ac = (– \(\sqrt{5}\))² – 4(\(\sqrt{5}\)) (\(\sqrt{5}\))
∴ b² – 4ac = 5 – 20
∴ b² – 4ac = –15
Since, b² – 4ac < 0
∴ The equation has no real roots.
(8) One of the roots of equation x² + mx – 5 = 0 is 2; find m.
(A) – 2
(B) – \(\large \frac {1}{2}\)
(C) \(\large \frac {1}{2}\)
(D) 2
Ans: Option (C) : \(\large \frac {1}{2}\)
Solution:
Since 2 is the one of the root of x² + mx – 5 = 0,
It satisfies the equation
Substituting x = 2 in the equation, we get,
(2)² + m(2) – 5 = 0
∴ 4 + 2m – 5 = 0
∴ 2m – 1 = 0
∴ 2m = 1
∴ m = \(\large \frac {1}{2}\)
2. Which of the following equations is quadratic?
(1) x² + 2x + 11 = 0
Solution:
x² + 2x + 11 = 0
Here, x is the only variable and maximum index of variable x is 2.
∴ It is a quadratic equation in variable x.
(2) x² – 2x + 5 = x²
Solution:
x² – 2x + 5 = x²
∴ x² – x² – 2x + 5 = 0
∴ – 2x + 5 = 0
Here, the maximum index of variable x is 1 and not 2.
∴ It is not a quadratic equation.
(3) (x + 2)² = 2x²
Solution:
(x + 2)² = 2x² …[Using (a + b)² = a² + 2ab + b²]
∴ x² + 4x + 4 = 2x²
∴ 2x² – x2 – 4x – 4 = 0
∴ x² – 4x – 4 = 0
Here, x is the only variable and maximum index of variable x is 2.
∴ It is a quadratic equation in variable x.
3. Find the value of discriminant for each of the following equations.
(1) 2y² – y + 2 = 0
Solution:
2y² – y + 2 = 0
Comparing with ay² + by + c = 0 we get,
a = 2, b = – 1, c = 2
∆ = b² – 4ac
∴ ∆ = (–1)² – 4 × 2 × 2
∴ ∆ = 1 – 16
∴ ∆ = – 15
(2) 5m² – m = 0
Solution:
5m² – m + 0 = 0
Comparing with am² + bm + c = 0 we get,
a = 5, b = – 1, c = 0
∆ = b² – 4ac
∴ ∆ = (– 1)² – 4 × 5 × 0
∴ ∆ = 1 – 0
∴ ∆ = 1
(3) \(\sqrt{5}\) x² – x – 5 = 0
Solution:
\(\sqrt{5}\) x² – x – 5 = 0
Comparing with ax² + bx + c = 0, we get,
a = \(\sqrt{5}\), b = – 1, c = – \(\sqrt{5}\)
∆ = b² – 4ac
∴ ∆ = (– 1)² – 4 × \(\sqrt{5}\) × – \(\sqrt{5}\)
∴ ∆ = 1 + 20
∴ ∆ = 21
4. One of the roots of the quadratic equation 2x² + kx – 2 = 0 is – 2, find k.
Solution:
x = – 2 is the root of the given quadratic equation.
∴ It satisfies the given equation.
Substituting x = – 2 in given equation,
2 (–2)² + k(– 2) – 2 = 0
∴ 2 × 4 – 2k – 2 = 0
∴ 8 – 2k – 2 = 0
∴ 6 – 2k = 0
∴ 2k = 6
∴ k = \(\large \frac {6}{2}\)
∴ k = 3
Ans: The value of k is 3.
5. Two roots of quadratic equations are given; frame the equation.
(1) 10 and – 10
Solution:
Let α and b are the roots of the quadratic equation
Let α = 10 and β = –10
α + β = 10 + (– 10) = 0 and
αβ = 10 × – 10 = – 100
The required quadratic equation is,
x² – (α + β)x + αβ = 0
∴ x² – (0)x + (–100) = 0
∴ x² – 100 = 0
Ans: The required quadratic equation is x² – 100 = 0
(2) 1 – 3\(\sqrt{5}\) and 1 + 3\(\sqrt{5}\)
Solution:
Let α and β are the roots of the quadratic equation, where, α = 1 – 3\(\sqrt{5}\) and β = 1 + 3\(\sqrt{5}\)
α + β = 1 – 3\(\sqrt{5}\) + 1 + 3\(\sqrt{5}\) = 2 and
αβ = (1 – 3\(\sqrt{5}\)) × (1 + 3\(\sqrt{5}\))
∴ αβ = (1)² – (3\(\sqrt{5}\))²
∴ αβ = 1 – 9(5)
∴ αβ = 1 – 45
∴ αβ = – 44
The required quadratic equation is,
x² – (α + β)x + αβ = 0
∴ x² – 2x – 44 = 0
Ans: The required quadratic equation is x² – 2x – 44 = 0
(3) 0 and 7
Solution:
Let a and b are the roots of the quadratic equation.
Let α = 0 and β = 7
α + β = 0 + 7 = 7 and
αβ = 0 × 7 = 0
The required quadratic equation is,
x² – (α + β)x + αβ = 0
∴ x² – 7x + 0 = 0
∴ x² – 7x = 0
Ans: The required quadratic equation is x² – 7x = 0
6. Determine the nature of roots for each of the quadratic equations.
(1) 3x² – 5x + 7 = 0
Solution:
3x² – 5x + 7 = 0
Comparing with ax² + bx + c = 0, we get,
a = 3, b = – 5, c = 7
∆ = b² – 4ac
∴ ∆ = (– 5)² – 4 × 3 × 7
∴ ∆ = 25 – 84
∴ ∆ = – 59
∵ ∆ < 0
∴ The roots of the quadratic equation are not real.
(2) \(\sqrt{3}\)x² + \(\sqrt{2}\)x – 2 \(\sqrt{3}\) = 0
Solution:
\(\sqrt{3}\)x² + \(\sqrt{2}\)x – 2 \(\sqrt{3}\) = 0
Comparing with ax² + bx + c = 0, we get,
a = \(\sqrt{3}\), b = \(\sqrt{2}\), c = – 2\(\sqrt{3}\)
∆ = b² – 4ac
∴ ∆ = (\(\sqrt{2}\))² – 4 × \(\sqrt{3}\) × (– 2\(\sqrt{3}\))
∴ ∆ = 2 + 8(3)
∴ ∆ = 2 + 24
∴ ∆ = 26
∵ ∆ > 0
∴ The roots of the quadratic equation are real and unequal.
(3) m² – 2m +1 = 0
Solution:
m² – 2m +1 = 0
Comparing with am² + bm + c = 0 we get,
a = 1, b = – 2, c = 1
∆ = b² – 4ac
∴ ∆ = (– 2)² – 4 × 1 × 1
∴ ∆ = 4 – 4
∴ ∆ = 0
∵ ∆ = 0
∴ The roots of the quadratic equation are real and equal.
7. Solve the following quadratic equations.
(1) \(\large \frac {1}{x\,+\,5}\) = \(\large \frac {1}{x²}\)
Solution:
\(\large \frac {1}{x\,+\,5}\) = \(\large \frac {1}{x²}\)
∴ x + 5 = x²
∴ x² – x – 5 = 0
Comparing with ax² + bx + c = 0 we get,
a = 1, b = – 1, c = – 5.
∴ b² – 4ac = (– 1)² – 4 × 1 × (– 5)
∴ b² – 4ac = 1 + 20
∴ b² – 4ac = 21
∴ x = \(\large \frac {-\,b\,±\,\sqrt{b²\,-\,4ac}}{2a}\)
∴ x = \(\large \frac {-\,(-\,1)\,±\,\sqrt{21}}{2(1)}\)
∴ x = \(\large \frac {1\,±\,\sqrt{21}}{2}\)
∴ x = \(\large \frac {1\,+\,\sqrt{21}}{2}\)
∴ x = \(\large \frac {1\,-\,\sqrt{21}}{2}\)
Ans: The roots of given quadratic equation are \(\large \frac {1\,+\,\sqrt{21}}{2}\) and \(\large \frac {1\,-\,\sqrt{21}}{2}\).
(2) x² – \(\large \frac {3x}{10}\) – \(\large \frac {1}{10}\) = 0
Solution:
x² – \(\large \frac {3x}{10}\) – \(\large \frac {1}{10}\) = 0
Multiplying both sides by 10 we get,
10x² – 3x – 1 = 0
∴ 10x² – 5x + 2x – 1 = 0
∴ 5x(2x – 1) + 1(2x – 1) = 0
∴ (2x – 1) (5x + 1) = 0
∴ 2x – 1 = 0 or 5x + 1 = 0
∴ 2x = 1 or 5x = –1
∴ x = \(\large \frac {1}{2}\) or x = \(\large \frac {-\,1}{5}\)
Ans: The roots of given quadratic equation are \(\large \frac {1}{2}\) or \(\large \frac {-\,1}{5}\)
(3) (2x + 3)² = 25
Solution:
(2x + 3)² = 25
∴ (2x + 3)² – 25 = 0
∴ (2x + 3)² – (5)² = 0
∴ (2x + 3 + 5) (2x + 3 – 5) = 0 …[a² – b² = (a + b)(a – b)]
∴ (2x + 8) (2x – 2) = 0
∴ 2x + 8 = 0 or 2x – 2 = 0
∴ 2x = – 8 or 2x = 2
∴ x = \(\large \frac {-\,8}{2}\) or x = \(\large \frac {2}{2}\)
∴ x = – 4 or x = 1
Ans: The roots of given quadratic equation are – 4 and 1.
(4) m² + 5m + 5 = 0
Solution:
m² + 5m + 5 = 0
Comparing with am² + bm + c = 0 we get,
a = 1, b = 5, c = 5.
∴ b² – 4ac = (– 5)² – 4 × 1 × 5
∴ b² – 4ac = 25 + 20
∴ b² – 4ac = 5
∴ m = \(\large \frac {-\,b\,±\,\sqrt{b²\,-\,4ac}}{2a}\)
∴ m = \(\large \frac {-\,5\,±\,\sqrt{5}}{2(1)}\)
∴ m = \(\large \frac {-\,5\,±\,\sqrt{5}}{2}\)
∴ m = \(\large \frac {-\,5\,+\,\sqrt{5}}{2}\)
∴ m = \(\large \frac {-\,5\,-\,\sqrt{5}}{2}\)
Ans: The roots of given quadratic equation are \(\large \frac {-\,5\,+\,\sqrt{5}}{2}\) and \(\large \frac {-\,5\,-\,\sqrt{5}}{2}\).
(5) 5m² + 2m + 1 =
Solution:
5m² + 2m + 1 = 0
Comparing with am² + bm + c = 0, we get,
a = 5, b = 2, c = 1.
∴ b² – 4ac = (2)² – 4 × 5 × 1
∴ b² – 4ac = 4 – 20
∴ b² – 4ac = – 16
∵ b² – 4ac < 0
∴ The roots of given quadratic equation are not real.
(6) x² – 4x – 3 = 0
Solution:
x² – 4x – 3 = 0
Comparing with am² + bm + c = 0 we get,
a = 1, b = – 4, c = – 3.
∴ b² – 4ac = (– 4)² – 4 × 1 × (– 3)
∴ b² – 4ac = 16 + 12
∴ b² – 4ac = 28
∴ x = \(\large \frac {-\,b\,±\,\sqrt{b²\,-\,4ac}}{2a}\)
∴ x = \(\large \frac {-\,(-\,4)\,±\,\sqrt{28}}{2(1)}\)
∴ x = \(\large \frac {4\,±\,4\sqrt{7}}{2}\)
∴ x = \(\large \frac {2(2\,±\,2\sqrt{7})}{2}\)
∴ x = 2 ± \(\sqrt{7}\)
∴ x = 2 + \(\sqrt{7}\)
∴ x = 2 – \(\sqrt{7}\)
Ans: The roots of given quadratic equation are 2 + \(\sqrt{7}\) and 2 – \(\sqrt{7}\).
8. Find m if (m – 12)x² + 2(m – 12) x + 2 = 0 has real and equal roots.
Solution:
(m – 12)x² + 2(m – 12) x + 2 = 0
Comparing with ax² + bx + c = 0, we get,
a = m – 12, b = 2(m – 12), c = 2
∆ = b² – 4ac
∴ ∆ = [2(m – 12)]² – 4 × (m – 12) × 2
∴ ∆ = 4(m² – 24m + 144) – 8(m – 12)
∴ ∆ = 4m² – 96m + 576 – 8m + 96
∴ ∆ = 4m² – 104m + 672
The roots are real and equal so ∆ must be zero.
4m² – 104m + 672 = 0
∴ m² – 26m + 168 = 0 …[Dividing both sides by 4]
∴ m² – 14m – 12m + 168 = 0
∴ m(m – 14) – 12(m – 14) = 0
∴ (m – 14) (m – 12) = 0
∴ m – 14 = 0 or m – 12 = 0
∴ m = 14 or m = 12
Since m – 12 = a and for a quadratic equation, a ≠ 0
∴ m ≠ 12
∴ m = 14
Ans: The value of m is 14.
9. The sum of two roots of a quadratic equation is 5 and the sum of their cubes is 35, find the equation.
Solution:
Let α and β are the roots of the quadratic equation.
Let α + β = 5 and α³ + β³ = 35 …[Given]
α³ + β³ = (α + β)³ – 3αβ(α + β)
∴ 35 = (5)³ – 3αβ(5)
∴ 35 = 125 – 15αβ
∴ 15αβ = 125 – 35
∴ 15αβ = 90
∴ αβ = \(\large \frac {90}{15}\)
∴ αβ = 6
The required quadratic equation is,
x² – (α + β)x + αβ = 0
∴ x² – 5x + 6 = 0
Ans: The required quadratic equation is x² – 5x + 6 = 0
10. Find quadratic equation such that its roots are square of sum of the roots and square of difference of the roots of equation 2x² + 2(p + q) x + p² + q² = 0
Solution:
2x² + 2(p + q) x + p² + q² = 0
Comparing with ax² + bx + c = 0, we get,
a = 2, b = 2(p + q), c = p² + q²
Let α and β are the roots of the quadratic equation.
α + β = \(\large \frac {-b}{a}\)
∴ α + β = \(\large \frac {-2(p + q)}{2}\)
∴ α + β = – (p + q) …(i)
and αβ = \(\large \frac {c}{a}\)
∴ αβ = \(\large \frac {p²\,+\,q²}{2}\) …(ii)
Let α₁ and β₁ are the roots of the quadratic equation.
α₁ = (α + β)² …[Given]
β₁ = (α – β)²
α₁ = [–(p + q)]² …[From (i)]
∴ α₁ = (p + q)² …(iii)
β₁ = (α – β)²
∴ β₁ = (α + β)² – 4αβ …[(a – b)² = (a + b)² – 4 ab]
∴ β₁ = [– (p + q)]² – 4 \(\large (\frac {p²\,+\,q²}{2})\)
∴ β₁ = (p + q)² – 2 (p² + q²)
∴ β₁ = p² + 2pq + q² – 2p² – 2q²
∴ β₁ = – p² + 2pq – q²
∴ β₁ = – (p² – 2pq + q²)
∴ β₁ = – (p – q)² …(iv)
Sum of the roots of the new equation,
= α₁ + β₁
= (p + q)² + [– (p – q)²] …[From (iii) and (iv)]
= p² + 2pq + q² – (p² – 2pq + q²)
= p² + 2pq + q² – p² + 2pq – q²
= 4pq
Product of roots of new equation
= α₁β₁
= (p + q)² [– (p – q)²] …[From (iii) and (iv)]
= – (p + q)² (p – q)²
= – [(p + q) (p – q)]²
= – (p² – q²)²
The required new equation is,
x² – (α₁ + β₁)x + α₁β₁ = 0
∴ x² – 4pqx + [– (p² – q²)²] = 0
∴ x² – 4pqx – (p² – q²)² = 0
Ans: The required new equation is x² – 4pqx – (p² – q²)² = 0
11. Mukund possesses ₹ 50 more than what Sagar possesses. The product of the amount they have is ₹ 15,000. Find the amount each one has.
Solution:
Let the amount with Sagar be ₹ x.
The amount with Mukund is = ₹ (x + 50)
According to given condition,
x × (x + 50) = 15000
∴ x² + 50x – 15000 = 0
∴ x² + 150x – 100x – 15000 = 0
∴ x(x + 150) – 100(x + 150) = 0
∴ (x + 150) (x – 100) = 0
∴ x + 150 = 0 or x – 100 = 0
∴ x = – 150 or x = 100
Now, x ≠ – 150 as amount in rupees cannot be negative.
∴ Amount with Sagar is x = 100
Amount with Mukurd is x + 50 = 100 + 50
∴ Amount with Mukurd = 150
Ans: The amount with Sagar is ₹ 100 and amount with Mukund is ₹ 150.
12. The difference between squares of two numbers is 120. The square of smaller number is twice the greater number. Find the numbers.
Solution:
Let the bigger number be x.
The difference between squares of two numbers is 120.
∴ Square of bigger number – Square of smaller number = 120
∴ x² – square of smaller number = 120
Square of smaller number = x² – 120
According to given condition,
x² – 120 = 2x
∴ x² – 2x – 120 = 0
∴ x² – 12x + 10x – 120 = 0
∴ x(x – 12) + 10(x – 12) = 0
∴ (x – 12) (x + 10) = 0
∴ x – 12 = 0 or x + 10 = 0
∴ x = 12 or x = –10
If bigger number is x = – 10, then,
Square of smaller number is x² – 120 = (– 10)² – 120
∴ Square of smaller number = 100 – 120
∴ Square of smaller number = – 20
x = – 10 is not acceptable because square of a smaller number cannot be negative.
∴ x = 12
Now,
Square of smaller number is x² – 120 = (12)² – 120
∴ Square of smaller number = 144 – 120
∴ Square of smaller number = 24
∴ Smaller number = ± \(\sqrt{24}\)
∴ Smaller number = \(\sqrt{24}\) or – \(\sqrt{24}\) …[Taking square root]
Ans: The required numbers are 12 and \(\sqrt{24}\) or 12 and – \(\sqrt{24}\).
13. Ranjana wants to distribute 540 oranges among some students. If 30 students were more each would get 3 oranges less. Find the number of students.
Solution:
Let the number of students be x.
Number of oranges = 540
∴ Number of oranges each student get = \(\large \frac {540}{x}\)
If there are (x + 30) students, then number of oranges each student get = \(\large \frac {540}{x\,+\,30}\)
According to given condition,
\(\large \frac {540}{x}\) – \(\large \frac {540}{x\,+\,30}\) = 3
∴ 540 \(\large (\frac {1}{x}\) – \(\large \frac {1}{x\,+\,30})\) = 3
∴ \(\large \frac {x\,+\,30\,-\,x}{x(x\,+\,30)}\) = \(\large \frac {3}{540}\)
∴ \(\large \frac {30}{x²\,+\,30x}\) = \(\large \frac {1}{180}\)
∴ x² + 30x = 5400
∴ x² + 30x – 5400 = 0
∴ x² + 90x – 60x – 5400 = 0
∴ x(x + 90) – 60(x + 90) = 0
∴ (x + 90) (x – 60) = 0
∴ x + 90 = 0 or x – 60 = 0
∴ x = – 90 or x = 60
Now, x ≠ – 90 as the number of students can not be negative.
∴ x = 60
Ans: The required number of students is 60.
14. Mr. Dinesh owns an agricultural farm at village Talvel. The length of the farm is 10 meter more than twice the breadth. In order to harvest rainwater, he dug a square shaped pond inside the farm. The side of the pond is \(\large \frac {1}{3}\) of the breadth of the farm. The area of the farm is 20 times the area of the pond. Find the length and breadth of the farm and of the pond.
Solution:
Let the breadth of the rectangular field is x m.
∴ Its length = (2x + 10) m
Area of the farm = (2x + 10) × x sq.m
Now,
Side of a square pond = \(\large \frac {1}{3}\) x m
∴ Side of a square pond = \(\large \frac {x}{3}\) m
Area of square pond = (side)²
∴ Area of square pond = \(\large (\frac {x}{3})\)²
∴ Area of square pond = \(\large \frac {x²}{9}\) sq. m
According to given condition,
(2x + 10) × x = 20 × \(\large \frac {x²}{9}\)
∴ 2x² + 10x = \(\large \frac {20\,x²}{9}\)
∴ 18x² + 90x = 20x²
∴ 90x = 20x² – 18x²
∴ 2x² – 90x = 0
∴ 2x(x – 45) = 0
∴ 2x = 0 or x – 45 = 0
∴ x = 0 or x = 45
Now, x ≠ 0 as the breadth of the field can not be zero.
∴ Breadth of the rectangular field is x = 45
Length of the field is,
(2x + 10) = 2 × 45 + 10
∴ (2x + 10) = 90 + 10
∴ (2x + 10) = 100 m
Also,
Side of the pond is \(\large \frac {x}{3}\) = \(\large \frac {45}{3}\)
∴ \(\large \frac {x}{3}\) = 15 m
Ans: The length of the rectangular field is 100 m and breadth is 45 m. Also, the length of each side of the square pond is 15 m.
15. A tank fills completely in 2 hours if both the taps are open. If only one of the taps is open at the given time, the smaller tap takes 3 hours more than the larger one to fill the tank. How much time does each tap take to fill the tank completely?
Solution:
Let bigger tap requires x hours to fill the tank.
The smaller tap requires (x + 3) hours.
According to given condition,
\(\large \frac {1}{x}\) + \(\large \frac {1}{x\,+\,3}\) = \(\large \frac {1}{2}\)
\(\large \frac {x\,+\,3\,+\,x}{x(x\,+\,3}\) = \(\large \frac {1}{2}\)
\(\large \frac {2x\,+\,3}{x²\,+\,3x}\) = \(\large \frac {1}{2}\)
2(2x + 3) = x² + 3x
4x + 6 = x² + 3x
x² + 3x – 4x – 6 = 0
x² + – x – 6 = 0
x² – 3x + 2x – 6 = 0
x(x – 3) + 2(x – 3) = 0
(x – 3) (x + 2) = 0
x – 3 = 0 or x + 2 = 0
x = 3 or x = – 2
Now, x ≠ – 2 as time cannot be negative.
∴ Hours required by the bigger tap to fill is x = 3 hours
Smaller tap takes (x + 3) hours = 3 + 3 = 6 hours
Ans: The bigger tap required 3 hours to fill the tank and the smaller tap required 6 hours.
