Chapter 1 – Similarity
Time - 25 Minutes
Marks - 10
1. All the questions are compulsory.
2. Read the question paper carefully.
3. Marks are included against each question.
4. Draw figures for each theorem.
1. Prove that in a triangle, the angle bisector divides the side opposite to the angle in the ratio of the remaining sides.
2. Prove that the ratio of the intercepts made on the transversal by three parallel lines is equal to the ratio of the corresponding intercepts made on any other transversal by the same parallel lines.
3. Complete the following activity: (2 marks)
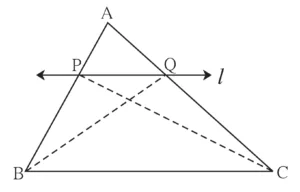
Theorem :
If a line parallel to a side of a triangle intersects the remaining sides in two distinct points, then the line divides the sides in the same proportion.
Given :
In ∆ABC line l || side BC and line l intersects AB and AC in point P and Q respectively
To prove :
\(\large \frac {AP}{PB}\) = \(\large \frac {AQ}{QC}\)
Construction :
Draw seg PC and seg BQ
Proof :
∆APQ and ∆PQB have equal heights.
∴ \(\large \frac {A (∆APQ)}{A (∆PQB)}\) = \(\large \frac {□}{PB}\) … (I) [areas proportionate to bases]
and
∴ \(\large \frac {A (∆APQ)}{A (∆PQC)}\) = \(\large \frac {AQ}{□}\) … (II) [areas proportionate to bases]
seg □ is the common base of ∆PQB and ∆PQC
Also, seg □ || seg BC,
Hence ∆PQB and ∆PQC have equal heights
A(∆PQB) = A(∆PQC) ………. (III)
∴ \(\large \frac {A (∆APQ)}{A (∆PQB)}\) = \(\large \frac {A (∆APQ)}{□}\) … [from (I), (II) and (III)]
\(\large \frac {AP}{PB}\) = \(\large \frac {AQ}{QB}\) … [from (I) and (II)]
Hence proved.
