Chapter 5 – Decimal Fractions
Practice set 14
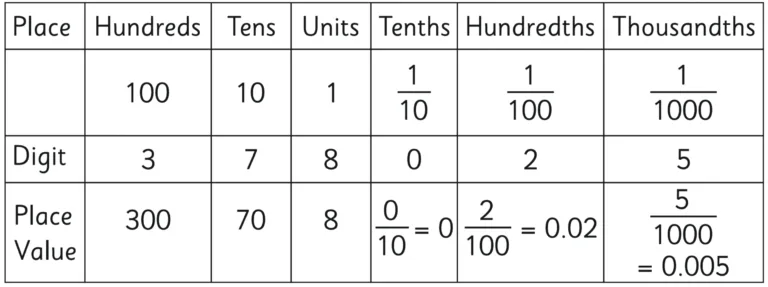
1. In the table below, write the place value of each of the digits in the number 378.025.
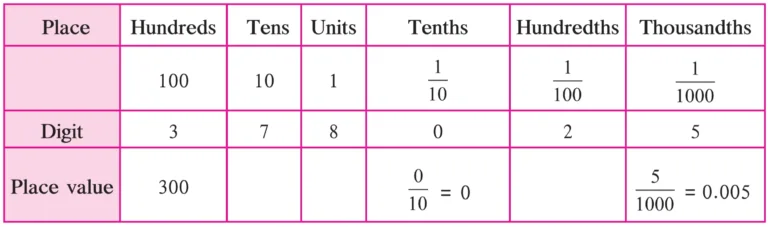
Solution:
2. Solve.
(1) 905.5 + 27.197
Solution:

Ans: 905.5 + 27.197 = 932.697
(2) 39 + 700.65
Solution:

Ans: 39 + 700.65 = 739.65
(3) 40 + 27.7 + 2.451
Solution:

Ans: 40 + 27.7 + 2.451 = 70.151
3. Subtract.
(1) 85.96 – 2.345
Solution:

Ans: 85.96 – 2.345 = 83.615
(2) 632.24 – 97.45
Solution:
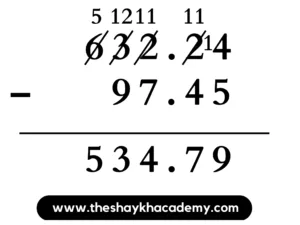
Ans: 632.24 – 97.45 = 534.79
(3) 200.005 – 17.186
Solution:

Ans: 200.005 – 17.186 = 182.819
4. Avinash travelled 42 km 365 m by bus, 12 km 460 m by car and walked 640 m. How many kilometres did he travel altogether? (Write your answer in decimal fractions.)
Solution:
Distance traveled in bus
= 42 km 365 m
= 42 km + \(\large \frac {365}{1000}\) km
= 42 km + 0.365 km
= 42.365 km
Distance travelled in car
= 12 km 460 m
= 12 km + \(\large \frac {460}{1000}\) km
= 12 km + 0.460 km
= 12.460 km
Distance walked
= 640 m
= \(\large \frac {640}{1000}\) km
= 0.640 km
∴ Total distance travelled
= Distance travelled in bus + Distance travelled in car + Distance walked
= 42.365 + 12.460 + 0.640
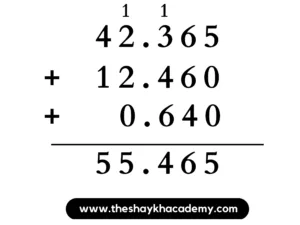
= 55.465 km
Ans: Distance travelled altogether by Avinash is 55.465 km.
5. Ayesha bought 1.80 m of cloth for her salwaar and 2.25 m for her kurta. If the cloth costs 120 rupees per metre, how much must she pay the shopkeeper?
Solution:
Total length of cloth bought by Ayesha
= 1.80 m + 2.25 m

= 4.05 m
Cost of 1 m of cloth = ₹120
∴ Cost of 4.05 m of cloth
= 4.05 × 120
= \(\large \frac {405}{100}\) × 120
= \(\large \frac {405\,×\,120}{100}\)
= \(\large \frac {48600}{100}\)
= \(\large \frac {486\,×\,100}{100}\)
= ₹ 486
Ans: Ayesha should pay ₹ 486 to the shopkeeper.
6. Sujata bought a watermelon weighing 4.25 kg and gave 1 kg 750g to the children in her neighbourhood. How much of it does she have left?
Solution:
Total weight of watermelon = 4.25 kg
Weight of watermelon given to children
= 1 kg 750 g
= 1 kg + \(\large \frac {750}{1000}\) kg
= 1 kg + 0.75 kg
= 1.75 kg
∴ Weight of watermelon left
= Total weight of watermelon – Weight of watermelon given to children
= 4.25 kg – 1.75 kg
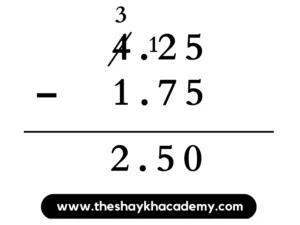
= 2.50 kg i.e. 2.5 kg
Ans: Weight of watermelon left with Sujata is 2.5 kg.
7. Anita was driving at a speed of 85.6 km per hour. The road had a speed limit of 55 km per hour. By how much should she reduce her speed to be within the speed limit?
Solution:
Speed at which Anita is driving = 85.6 km per hr.
Speed limit = 55 km per hr.
∴ Anita should reduce her speed by
= 85.6 km per hour – 55 km per hour

= 30.6 km per hour
Ans: Anita should reduce her speed by 30.6 km per hour to be within the speed limit.
Practice set 15
1. Write the proper number in the empty boxes.
(1) \(\large \frac {3}{5}\) = \(\large \frac {3\,×\,□}{5\,×\,□}\) = \(\large \frac {□}{10}\) = □
Solution:
\(\large \frac {3}{5}\) = \(\large \frac {3\,×\,2}{5\,×\,2}\) = \(\large \frac {6}{10}\) = 0.6
(2) \(\large \frac {25}{8}\) = \(\large \frac {25\,×\,□}{8\,×\,125}\) = \(\large \frac {□}{1000}\) = 3.125
Solution:
\(\large \frac {25}{8}\) = \(\large \frac {25\,×\,125}{8\,×\,125}\) = \(\large \frac {3125}{1000}\) = 3.125
(3) \(\large \frac {21}{2}\) = \(\large \frac {21\,×\,□}{2\,×\,□}\) = \(\large \frac {□}{10}\) = □
Solution:
\(\large \frac {21}{2}\) = \(\large \frac {21\,×\,5}{2\,×\,5}\) = \(\large \frac {105}{10}\) = 10.5
(4) \(\large \frac {22}{40}\) = \(\large \frac {11}{20}\) = \(\large \frac {11\,×\,□}{20\,×\,5}\) = \(\large \frac {□}{100}\) = □
Solution:
\(\large \frac {22}{40}\) = \(\large \frac {11}{20}\) = \(\large \frac {11\,×\,5}{20\,×\,5}\) = \(\large \frac {55}{100}\) = 0.55
2. Convert the common fractions into decimal fractions.
(1) \(\large \frac {3}{4}\)
Solution:
\(\large \frac {3}{4}\)
= \(\large \frac {3\,×\,25}{4\,×\,25}\)
= \(\large \frac {75}{100}\)
= 0.75
Ans: \(\large \frac {3}{4}\) = 0.75
(2) \(\large \frac {4}{5}\)
Solution:
\(\large \frac {4}{5}\)
= \(\large \frac {4\,×\,2}{5\,×\,2}\)
= \(\large \frac {8}{10}\)
= 0.8
Ans: \(\large \frac {4}{5}\) = 0.8
(3) \(\large \frac {9}{8}\)
Solution:
\(\large \frac {9}{8}\)
= \(\large \frac {9\,×\,125}{8\,×\,125}\)
= \(\large \frac {1125}{1000}\)
= 1.125
Ans: \(\large \frac {9}{8}\) = 1.125
(4) \(\large \frac {17}{20}\)
Solution:
\(\large \frac {17}{20}\)
= \(\large \frac {17\,×\,5}{20\,×\,5}\)
= \(\large \frac {85}{100}\)
= 0.85
Ans: \(\large \frac {17}{20}\) = 0.85
(5) \(\large \frac {36}{40}\)
Solution:
\(\large \frac {36}{40}\)
= \(\large \frac {18}{20}\)
= \(\large \frac {18\,×\,5}{20\,×\,5}\)
= \(\large \frac {90}{100}\)
= 0.9
Ans: \(\large \frac {36}{40}\) = 0.9
(6) \(\large \frac {7}{25}\)
Solution:
\(\large \frac {7}{25}\)
= \(\large \frac {7\,×\,4}{25\,×\,4}\)
= \(\large \frac {28}{100}\)
= 0.28
Ans: \(\large \frac {7}{25}\) = 0.28
(7) \(\large \frac {19}{200}\)
Solution:
\(\large \frac {19}{20}\)
= \(\large \frac {19\,×\,5}{200\,×\,5}\)
= \(\large \frac {95}{1000}\)
= 0.095
Ans: \(\large \frac {19}{20}\) = 0.095
3. Convert the decimal fractions into common fractions.
(1) 27.5
Solution:
27.5 = \(\large \frac {27.5}{10}\)
(2) 0.007
Solution:
0.007 = \(\large \frac {7}{1000}\)
(3) 90.8
Solution:
90.8 = \(\large \frac {90.8}{10}\)
(4) 39.15
Solution:
39.15 = \(\large \frac {3915}{100}\)
(5) 3.12
Solution:
3.12 = \(\large \frac {312}{100}\)
(6) 70.400
Solution:
70.400 = 70.4 = \(\large \frac {704}{10}\)
Practice set 16
1. If, 317 × 45 = 14265, then 3.17 × 4.5 = ?
Solution:
If, 317 × 45 = 14265,
then, 3.17 × 4.5 = 14.265
2. If, 503 × 217 = 109151, then 5.03 × 2.17 = ?
Solution:
If, 503 × 217 = 109151,
then 5.03 × 2.17 = 1.0951
3. Multiply.
(1) 2.7 × 1.4
Solution:

Ans: 2.7 × 1.4 = 3.78
(2) 6.17 × 3.9
Solution:

Ans: 5.04 × 0.7 = 24.063
(3) 0.57 × 2
Solution:
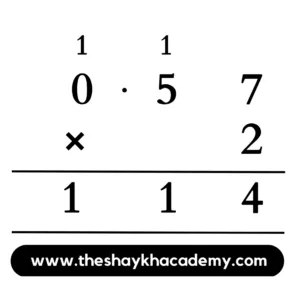
Ans: 0.57 × 2 = 1.14
(4) 5.04 × 0.7
Solution:
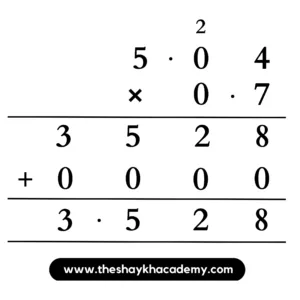
Ans: 5.04 × 0.7 = 3.528
4. Virendra bought 18 bags of rice, each bag weighing 5.250 kg. How much rice did he buy altogether? If the rice costs 42 rupees per kg, how much did he pay for it?
Solution:
Weight of one bag of rice = 5.250 kg = 5.25 kg
Number of bags of rice = 18
∴ Total Weight
= 18 × 5.25
= 18 × \(\large \frac {525}{100}\)
= \(\large \frac {18\,×\,525}{100}\)
= \(\large \frac {945}{100}\)
= 9.45 kg
Cost of 1 kg of rice = Rs 42
∴ Cost of 94.5 kg of rice
= 42 × 94.5
= 42 × \(\large \frac {945}{10}\)
= \(\large \frac {42\,×\,945}{10}\)
= \(\large \frac {39690}{10}\)
= ₹ 3969
Ans: Total rice bought by Virendra is 94.5 kg, and the amount paid for it is ₹ 3969.
5. Vedika has 23.50 metres of cloth. She used it to make 5 curtains of equal size. If each curtain required 4 metres 25 cm to make, how much cloth is left over?
Solution:
Cloth required to make 1 curtain
= 4 m 25 cm
= 4 m + \(\large \frac {25}{100}\)
= 4 m + 0.25 m
= 4.25 m
∴ Cloth required to make 5 curtains
= 5 × 4.25
= 5 × \(\large \frac {425}{100}\)
= \(\large \frac {5\,×\,425}{100}\)
= \(\large \frac {2125}{100}\)
= 21.25 m
Cloth remaining with Vedika
= Total cloth with Vedika – Cloth used
= 23.5 m – 21.25 m

= 2.25 m
Ans: The length of cloth remaining with Vedika is 2.25 m.
Practice set 17
1. Carry out the following divisions.
(1) 4.8 ÷ 2
Solution:
4.8 ÷ 2
= \(\large \frac {48}{10}\) ÷ \(\large \frac {2}{1}\)
= \(\large \frac {48}{10}\) × \(\large \frac {1}{2}\)
= \(\large \frac {48\,×\,1}{10\,×\,2}\)
= \(\large \frac {24}{10}\)
= 2.4
Ans: 4.8 ÷ 2 = 2.4
(2) 17.5 ÷ 5
Solution:
17.5 ÷ 5
= \(\large \frac {175}{10}\) ÷ \(\large \frac {5}{1}\)
= \(\large \frac {175}{10}\) × \(\large \frac {1}{5}\)
= \(\large \frac {175\,×\,1}{10\,×\,5}\)
= \(\large \frac {35}{10}\)
= 3.5
Ans: 17.5 ÷ 5 = 3.5
(3) 20.6 ÷ 2
Solution:
20.6 ÷ 2
= \(\large \frac {206}{10}\) ÷ \(\large \frac {2}{1}\)
= \(\large \frac {206}{10}\) × \(\large \frac {1}{2}\)
= \(\large \frac {206\,×\,1}{10\,×\,2}\)
= \(\large \frac {103}{10}\)
= 10.3
Ans: 20.6 ÷ 2 = 10.3
(4) 32.5 ÷ 25
Solution:
32.5 ÷ 25
= \(\large \frac {325}{10}\) ÷ \(\large \frac {25}{1}\)
= \(\large \frac {325}{10}\) × \(\large \frac {1}{25}\)
= \(\large \frac {325\,×\,1}{10\,×\,25}\)
= \(\large \frac {13}{10}\)
= 1.3
Ans: 32.5 ÷ 25 = 1.3
2. A road is 4 km 800 m long. If trees are planted on both its sides at intervals of 9.6 m, how many trees were planted?
Solution:
Length of road
= 4 km 800 m
= 4 km + \(\large \frac {800}{1000}\) km
= 4 km + 0.8 km
= 4.8 km
= 4.8 × 1000 m
= 4800 m
Number of trees on one side
= 4800 ÷ 9.6
= 4800 ÷ \(\large \frac {96}{10}\)
= 4800 × \(\large \frac {10}{96}\)
= 50 × 10
= 500
∴ Number of trees on both sides
= 2 × number of trees on one side
= 2 × 500
= 1000
If the trees are planted at the beginning of the road, then the total number of trees
= 1000 + 2
= 1002 trees
Ans: Total number of trees planted is 1000 or 1002.
3. Pradnya exercises regularly by walking along a circular path on a field. If she walks a distance of 3.825 km in 9 rounds of the path, how much does she walk in one round?
Solution:
Total distance walked in 9 rounds = 3.825 km
∴ Distance walked in 1 round
= \(\large \frac {3825}{1000}\) ÷ \(\large \frac {9}{1}\)
= \(\large \frac {3825}{1000}\) × \(\large \frac {1}{9}\)
= \(\large \frac {425}{1000}\)
= 0.425
Ans: Total distance walked in 1 round is 0.425 km.
4. A pharmaceutical manufacturer bought 0.25 quintal of hirada, a medicinal plant, for 9500 rupees. What is the cost per quintal of hirada? (1 quintal = 100 kg)
Solution:
Cost of 0.25 quintal of hirada = ₹ 9500
∴ Cost of 1 quintal of hirada
= 9500 ÷ 0.25
= 9500 ÷ \(\large \frac {25}{100}\)
= 9500 × \(\large \frac {100}{25}\)
= 380 × 100
= ₹ 38,000
Ans: Cost per quintal of hirada is Rs 38,000.
