Miscellaneous Problems : Set 2
1. Angela deposited 15000 rupees in a bank at a rate of 9 p.c.p.a. She got simple interest amounting to 5400 rupees. For how many years had she deposited the amount?
Given:
P = ₹ 15000
R = 9 p.c.p.a
Simple Interest = ₹ 17400
To find:
No of years
Solution:
Total interest = \(\large \frac{P\, ×\, R\, ×\, T}{100} \)
∴ 5400 = \( \large \frac{15000\, ×\, 9\, ×\, T}{100} \)
∴ 5400 = 150 × 9 × T
∴ 5400 = 1350 × T
∴ \( \large \frac{5400}{1350} \) = T
∴ T = 4 years
Ans: Angela had deposited the amount for 4 years.
2. Ten men take 4 days to complete the task of tarring a road. How many days would 8 men take?
Solution:
10 men take 4 days to tar the road
∴ 8 men would take ? hours to tar the road
Let 8 men take x days to tar the road
The number of men and the number of days required to tar the road are in inverse proportion
∴ 8 × x = 10 x 4
∴ 8x = 40
∴ x = \(\large \frac {40}{8}\)
∴ x = 5
Ans: 8 men will require 5 days to tar the road.
3. Nasruddin and Mahesh invested ₹ 40,000 and ₹ 60,000 respectively to start a business. They made a profit of 30%. How much profit did each of them make?
Given:
Nasruddin invested for business = ₹ 40,000
Mahesh invested for business = ₹ 60,000
Profit made by them = 30%
Solution:
Total amount invested by Nasruddin and Mahesh = ₹ 40,000 + ₹ 60,000
∴ Total amount invested by Nasruddin and Mahesh = Rs 1,00,000
Profit earned by them = 30%
∴ Total profit = 30% of 100000
∴ Total profit = \(\large \frac {30}{100}\) × 100000
∴ Total profit = ₹ 30000
Proportion of investment = 40000 : 60000
∴ Proportion of investment = 2 : 3 …[Dividing by 20000]
Let Nasruddin’s profit be Rs 2x and Mahesh’s profit be Rs 3x.
∴ 2x + 3x = 30000
∴ 5x = 30000
∴ x = \(\large \frac {30000}{5}\)
∴ x = 6000
So,
Nasruddin’s profit = 2x
∴ Nasruddin’s profit = 2 × 6000
∴ Nasruddin’s profit = ₹ 12000
And, Mahesh’s profit = 3x = 3 × 6000 = Rs 18000
∴ Mahesh’s profit = 3 × 6000
∴ Mahesh’s profit = ₹ 18000
Ans: The profit of Nasruddin is ₹ 12000 and that of Mahesh is ₹ 18000.
4. The diameter of a circle is 5.6 cm. Find its circumference.

Given:
Diameter of the circle = 5.6 cm
To find:
Circumference of the circle
Solution:
Circumference of the circle = πd
∴ Circumference of the circle = \(\large \frac {22}{7}\) × 5.6
∴ Circumference of the circle = 22 × 0.8
∴ Circumference of the circle = 17.6 cm
Ans: The circumference of the circle is 17.6 cm.
5. Expand.
(i) (2a – 3b)²
Solution:
Here,
a = 2a and b = 3b
We know that,
(a – b)² = a² – 2ab + b²
∴ (2a – 3b)² = (2a)² – 2 × 2a × 3b + (3b)²
∴ (2a – 3b)² = 4a² – 12ab + 9b²
Ans: (2a – 3b)² = 4a² – 12ab + 9b²
(ii) (10 + y)²
Solution:
Here,
a = 10 and b = y
We know that,
(a + b)² = a² + 2ab + b²
∴ (10 – y)² = (10)² + 2 × 10 × y + (y)²
∴ (10 – y)² = 100 + 20y + y²
Ans: (10 – y)² = 100 + 20y + y²
(iii) \((\large \frac {p}{3} + \large \frac {q}{4})\)²
Solution:
Here,
a = \(\large \frac {p}{3}\) and b = \(\large \frac {q}{4}\)
We know that,
(a + b)² = a² + 2ab + b²
∴ \((\large \frac {p}{3} + \large \frac {q}{4})\)² = (\(\large \frac {p}{3}\))² + 2 × \(\large \frac {p}{3}\) × \(\large \frac {q}{4}\) + (\(\large \frac {q}{4}\))²
∴ \((\large \frac {p}{3} + \large \frac {q}{4})\)² = \(\large \frac {p²}{9}\) + \(\large \frac {pq}{6}\)+ \(\large \frac {q²}{16}\)
Ans: \((\large \frac {p}{3} + \large \frac {q}{4})\)² = \(\large \frac {p²}{9}\) + \(\large \frac {pq}{6}\)+ \(\large \frac {q²}{16}\)
(iv) \((y \, – \large \frac {3}{y})\)²
Solution:
Here,
a = y and b = \(\large \frac {3}{y}\)
We know that,
(a – b)² = a² – 2ab + b²
∴ \((y \, – \large \frac {3}{y})\)² = (y)² – 2 × y × \(\large \frac {3}{y}\) + \((\large \frac {3}{y})\)²
∴ \((y \, – \large \frac {3}{y})\)² = y² – 6 + \(\large \frac {9}{y²}\)
Ans: \((y \, – \large \frac {3}{y})\)² = y² – 6 + \(\large \frac {9}{y²}\)
6. Use a formula to multiply.
(i) (x – 5) (x + 5)
Solution:
Here, a = x and b = 5
We know that,
(a + b)(a – b) = a² – b²
∴ (x – 5) (x + 5) = x² – 5²
∴ (x – 5) (x + 5) = x² – 25
Ans: (x – 5) (x + 5) = x² – 25
(ii) (2a – 13) (2a + 13)
Solution:
Here, a = 2a and b = 13
We know that,
(a + b)(a – b) = a² – b²
∴ (2a – 13) (2a + 13) = (2a)² – 13²
∴ (2a – 13) (2a + 13) = 4a² – 169
Ans: (2a – 13) (2a + 13) = 4a² – 169
(iii) (4z – 5y) (4z + 5y)
Solution:
Here, a = 4z and b = 5y
We know that,
(a + b)(a – b) = a² – b²
∴ (4z – 5y) (4z + 5y) = (4z)² – (5y)²
∴ (4z – 5y) (4z + 5y) = 16z² – 25y²
Ans: (4z – 5y) (4z + 5y) = 16z² – 25y²
(iv) (2t – 5) (2t + 5)
Solution:
Here, a = 2t and b = 5
We know that,
(a + b)(a – b) = a² – b²
∴ (2t – 5) (2t + 5) = (2t)² – 5²
∴ (2t – 5) (2t + 5) = 4t² – 25
Ans: (2t – 5) (2t + 5) = 4t² – 25
7. The diameter of the wheel of a cart is 1.05 m. How much distance will the cart cover in 1000 rotations of the wheel?
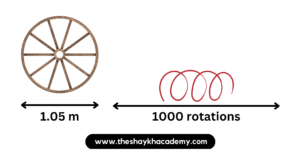
Given:
Diameter of the wheel = 1.05 m
No of rotations = 1000
To find:
Distance covered by cart in 1000 rotations
Solution:
Distance covered by cart in 1 rotation = Circumference of the wheel
∴ Distance covered by cart in 1 rotation = πd
∴ Distance covered by cart in 1 rotation = \(\large \frac {22}{7}\) × 1.05
∴ Distance covered by cart in 1 rotation = 3.3 m
Now,
Distance covered by cart in 1000 rotations = 1000 × 3.3 m
∴ Distance covered by cart in 1000 rotations = 3300 m
∴ Distance covered by cart in 1000 rotations = \(\large \frac {3300}{1000}\) km …[∵ 1 km = 1000 m]
∴ Distance covered by cart in 1000 rotations = 3.3 km
Ans: The distance covered by the cart in 1000 rotations of the wheel is 3.3 km.
8. The area of a rectangular garden of length 40 m, is 1000 sq m. Find the breadth of the garden and its perimeter. The garden is to be enclosed by 3 rounds of fencing, leaving an entrance of 4 m. Find the cost of fencing the garden at a rate of 250 rupees per metre.
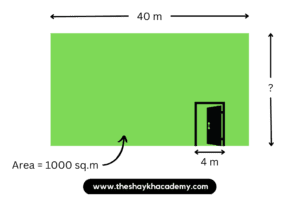
Given:
Length of the rectangular garden = 40 m
Area of the rectangular garden = 1000 sq. m.
Rate of fencing the garden = ₹ 250 per m.
To find:
Breadth of the garden
Perimeter of the garden
Cost of fencing the garden
Solution:
Area of the rectangular garden = length of the garden × breadth of the garden
∴ 1000 = 40 × breadth of the garden
∴ \(\large \frac {1000}{40}\) = breadth of the garden
∴ breadth of the garden = 25 m
Perimeter of the garden = 2 × length of the garden + 2 × breadth of the garden
∴ Perimeter of the garden = 2 × 40 + 2 × 25
∴ Perimeter of the garden = 80 + 50
∴ Perimeter of the garden = 130 m
Now,
Length of one round of fence = Perimeter of the garden – width of the entrance
∴ Length of one round of fence = 130 – 4
∴ Length of one round of fence = 126 m
Total length of fencing = Length of one round of fencing × number of rounds
∴ Total length of fencing = 126 × 3
∴ Total length of fencing = 378 m
And,
Total cost of fencing = Total length of fencing × rate of fencing the garden
Total cost of fencing = 378 × 250
Total cost of fencing = ₹ 94500
Ans: The cost of fencing the garden is ₹ 94500.
9. From the given figure, find the length of hypotenuse AC and the perimeter of ∆ABC.
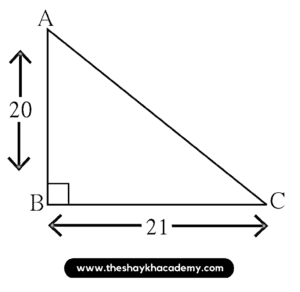
Given:
AB = 20 units
BC = 21 units
∠ABC = 90°
To find:
The value of x
Solution:
In ∆ABC, ∠ABC = 90°
∴ Side AC is the hypotenuse
According to Pythagoras’ theorem,
l(AC)² = l(AB)² + l(BC)²
∴ l(AC)² = 20² + 21²
∴ l(AC)² = 400 + 441
∴ l(AC)² = 841
∴ l(AC)² = 29²
∴ l(AC) = 29 units
Perimeter of ∆ABC = l(AB) + l(BC) + l(AC)
∴ Perimeter of ∆ABC = 20 + 21 + 29
∴ Perimeter of ∆ABC = 70 units
Ans: Perimeter of ∆ABC is 70 units.
10. If the edge of a cube is 8 cm long, find its total surface area.
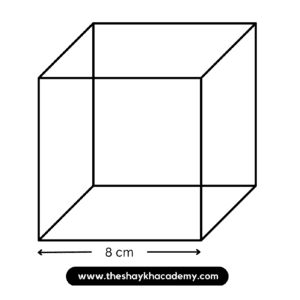
Given:
Side = 8 cm
To find:
Total surface area of cube
Solution:
Total surface area of the cube = 6l²
∴ Total surface area of the cube = 6 × (8)²
∴ Total surface area of the cube = 6 × 64
∴ Total surface area of the cube = 384 sq. m.
Ans: Total surface area of the cube is 385 sq. m.
11. Factorise :
365y⁴z³ – 146y²z⁴
Solution:
365y⁴z³ – 146y²z⁴ = 73 (5y⁴z³ – 2y²z⁴)
∴ 365y⁴z³ – 146y²z⁴ = 73y² (5y²z³ – 2z⁴)
∴ 365y⁴z³ – 146y²z⁴ = 73y²z³ (5y² – 2z)
Ans: 365y⁴z³ – 146y²z⁴ = 73y²z³ (5y² – 2z)
Multiple Choice Questions
Choose the right answers from the options given for each of the following questions.
1. If the average of the numbers 33, 34, 35, x, 37, 38, 39 is 36, what is the value of x ?
(i) 40
(ii) 32
(iii) 42
(iv) 36
Solution:
We know that,
Average = \( \large \frac{\text { Sum of all scores in the given data }}{\text { Total number of scores }}\)
∴ 36 = \(\large \frac{33\, +\, 34\, +\, 35\, +\, x\, +\, 37\, +\, 38\, +\, 39}{7}\)
∴ 36 × 7 = 216 + x
∴ 252 = 216 + x
∴ 252 – 216 = x
∴ x = 36
OPTION (iv) : 36
2. The difference of the squares, (61² – 51²) is equal to ……………… .
(i) 1120
(ii) 1230
(iii) 1240
(iv) 1250
Solution:
In (61² – 51²),
a = 61 and b = 51
We know that,
a² – b² = (a + b)(a – b)
∴ 61² – 51² = (61 + 51)(61 – 51)
∴ 61² – 51² = (112)(10)
∴ 61² – 51² = 1120
OPTION (i) : 1120
3. If 2600 rupees are divided between Sameer and Smita in the proportion 8 : 5, the share of each is …………… and …………… respectively.
(i) ₹ 1500, ₹ 1100
(ii) ₹ 1300, ₹ 900
(iii) ₹ 800, ₹ 500
(iv) ₹ 1600, ₹ 1000
Solution:
₹ 2600 is to be divided among Sameer and Smita in the ratio = 8 : 5
Total = 8 + 5 = 13
∴ Sameer’s share = \(\large \frac {8}{13}\) × 2600
∴ Sameer’s share = ₹ 1600
Ans,
Smita’s share = \(\large \frac {5}{13}\) × 2600
∴ Smita’s share = ₹ 1000
OPTION (iv) : ₹ 1600, ₹ 1000
