Chapter 6 – Indices
Practice Set 26
1. Complete the table below.
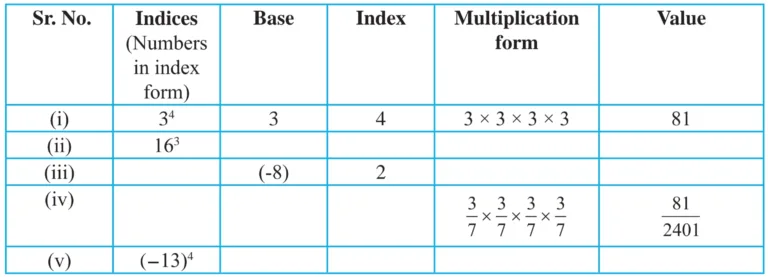
Solution:

2. Find the value.
(i) 2¹⁰
Solution:
2¹⁰
= 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 1024
Ans: 2¹⁰ = 1024
(ii) 5³
Solution:
5³
= 5 × 5 × 5
= 125
Ans: 5³ = 125
(iii) (– 7)⁴
Solution:
(– 7)⁴
= (– 7) × (– 7) × (– 7) × (– 7)
= 2401
Ans: (– 7)⁴ = 2401
(iv) (– 6)³
Solution:
(– 6)³
= (– 6) × (– 6) × (– 6)
= – 216
Ans: (– 6)³ = – 216
(v) 9³
Solution:
9³
= 9 × 9 × 9
= 729
Ans: 9³ = 729
(vi) 8¹
Solution:
8¹
= 8
Ans: 8¹ = 8
(vii) \(\large (\frac {4}{5})\)³
Solution:
\(\large (\frac {4}{5})\)³
= \(\large (\frac {4}{5})\) × \(\large (\frac {4}{5})\) × \(\large (\frac {4}{5})\)
= \(\large \frac {64}{25}\)
Ans: \(\large (\frac {4}{5})\)³ = \(\large \frac {64}{25}\)
(viii) \(\large (\frac {–\,1}{2})\)⁴
Solution:
\(\large (\frac {–\,1}{2})\)⁴
= \(\large (\frac {–\,1}{2})\) × \(\large (\frac {–\,1}{2})\) × \(\large (\frac {–\,1}{2})\) × \(\large (\frac {–\,1}{2})\)
= \(\large \frac {1}{16}\)
Ans: \(\large (\frac {–\,1}{2})\)⁴ = \(\large \frac {1}{16}\)
Practice Set 27
(1) Simplify.
(i) 7⁴ × 7²
Solution:
7⁴ × 7²
= 7⁴⁺² …[∵ aᵐ × aⁿ = aᵐ⁺ⁿ]
= 7⁶
(ii) (– 11)⁵ × (– 11)²
Solution:
(– 11)⁵ × (– 11)²
= (– 11)⁵⁺² …[∵ aᵐ × aⁿ = aᵐ⁺ⁿ]
= (– 11)⁷
(iii) \(\large (\frac {6}{7})\)³ × \(\large (\frac {6}{7})\)⁵
Solution:
\(\large (\frac {6}{7})\)³ × \(\large (\frac {6}{7})\)⁵
= \(\large (\frac {6}{7})\)³⁺⁵ …[∵ aᵐ × aⁿ = aᵐ⁺ⁿ]
= \(\large (\frac {6}{7})\)⁸
(iv) \(\large (–\,\frac {3}{2})\)⁵ × \(\large (–\,\frac {3}{2})\)³
Solution:
\(\large (–\,\frac {3}{2})\)⁵ × \(\large (–\,\frac {3}{2})\)³
= \(\large (–\,\frac {3}{2})\)⁵⁺³ …[∵ aᵐ × aⁿ = aᵐ⁺ⁿ]
= \(\large (–\,\frac {3}{2})\)⁸
(v) a¹⁶ × a⁷
Solution:
a¹⁶ × a⁷
= a¹⁶⁺⁷ …[∵ aᵐ × aⁿ = aᵐ⁺ⁿ]
= a²³
(vi) \(\large (\frac {P}{5})\)³ × \(\large (\frac {P}{5})\)⁷
Solution:
\(\large (\frac {P}{5})\)³ × \(\large (\frac {P}{5})\)⁷
= \(\large (\frac {P}{5})\)³⁺⁷ …[∵ aᵐ × aⁿ = aᵐ⁺ⁿ]
= \(\large (\frac {P}{5})\)¹⁰
Practice Set 28
1. Simplify.
(i) a⁶ ÷ a⁴
Solution:
a⁶ ÷ a⁴
= a⁶⁻⁴ …[∵ \(\large \frac {aᵐ}{aⁿ}\) = aᵐ⁻ⁿ]
= a²
Ans: a⁶ ÷ a⁴ = a²
(ii) m⁵ ÷ m⁸
Solution:
m⁵ ÷ m⁸
= m⁵⁻⁸ …[∵ \(\large \frac {aᵐ}{aⁿ}\) = aᵐ⁻ⁿ]
= m³
Ans: m⁵ ÷ m⁸ = m³
(iii) p³ ÷ p¹³
Solution:
p³ ÷ p¹³
= p³⁻¹³ …[∵ \(\large \frac {aᵐ}{aⁿ}\) = aᵐ⁻ⁿ]
= p⁻¹⁰
Ans: p³ ÷ p¹³ = p⁻¹⁰
(iv) x¹⁰ ÷ x¹⁰
Solution:
x¹⁰ ÷ x¹⁰
= x¹⁰⁻¹⁰ …[∵ \(\large \frac {aᵐ}{aⁿ}\) = aᵐ⁻ⁿ]
= x⁰
= 1 …[∵ a⁰ = 1]
Ans: x¹⁰ ÷ x¹⁰ = 1
2. Find the value.
(i) (– 7)¹² ÷ (– 7)¹²
Solution:
(– 7)¹² ÷ (– 7)¹²
= (– 7)¹²⁻¹² …[∵ aᵐ ÷ aⁿ = aᵐ⁻ⁿ]
= (– 7)⁰
= 1 …[∵ a⁰ = 1]
Ans: (– 7)¹² ÷ (– 7)¹² = 1
(ii) 7⁵ ÷ 7³
Solution:
7⁵ ÷ 7³
= 7⁵⁻³ …[∵ aᵐ ÷ aⁿ = aᵐ⁻ⁿ]
= 7²
= 7 × 7
= 49
Ans: 7⁵ ÷ 7³ = 49
(iii) \(\large (\frac {4}{5})\)³ ÷ \(\large (\frac {4}{5})\)²
Solution:
\(\large (\frac {4}{5})\)³ ÷ \(\large (\frac {4}{5})\)²
= \(\large (\frac {4}{5})\)³⁻² …[∵ aᵐ ÷ aⁿ = aᵐ⁻ⁿ]
= \(\large (\frac {4}{5})\)
Ans: \(\large (\frac {4}{5})\)³ ÷ \(\large (\frac {4}{5})\)² = \(\large (\frac {4}{5})\)
(iv) 4⁷ ÷ 4⁵
Solution:
4⁷ ÷ 4⁵
= 4⁷⁻⁵ …[∵ aᵐ ÷ aⁿ = aᵐ⁻ⁿ]
= 4²
= 4 × 4
= 16
Ans: 4⁷ ÷ 4⁵ = 16
Practice Set 29
1. Simplify.
(i) \(\large [(\frac {15}{12})³]⁴\)
Solution:
\(\large [(\frac {15}{12})³]⁴\)
= \(\large (\frac {15}{12})³ˣ⁴\) …[∵ (aᵐ)ⁿ = aᵐⁿ]
= \(\large (\frac {15}{12})¹²\)
Ans: \(\large [(\frac {15}{12})³]⁴\) = \(\large (\frac {15}{12})¹²\)
(ii) (3⁴)⁻²
Solution:
(3⁴)⁻²
= (3⁴ˣ⁻²) …[∵ (aᵐ)ⁿ = aᵐⁿ]
= 3⁻⁸
Ans: (3⁴)⁻² = 3⁻⁸
(iii) \(\large [(\frac {1}{7})⁻³]⁴\)
Solution:
\(\large [(\frac {1}{7})⁻³]⁴\)
= \(\large (\frac {1}{7})⁻³ˣ⁴\) …[∵ (aᵐ)ⁿ = aᵐⁿ]
= \(\large (\frac {1}{7})⁻¹²\)
Ans: \(\large [(\frac {1}{7})⁻³]⁴\) = \(\large (\frac {1}{7})⁻¹²\)
(iv) \(\large [(\frac {2}{5})⁻²]⁻³\)
Solution:
\(\large [(\frac {2}{5})⁻²]⁻³\)
= \(\large (\frac {2}{5})⁻²ˣ⁻³\) …[∵ (aᵐ)ⁿ = aᵐⁿ]
= \(\large (\frac {2}{5})⁶\)
Ans: \(\large [(\frac {2}{5})⁻²]⁻³\) = \(\large (\frac {2}{5})⁶\)
(v) (6⁵)⁴
Solution:
(6⁵)⁴
= (6⁵ˣ⁴) …[∵ (aᵐ)ⁿ = aᵐⁿ]
= 6²⁰
Ans: (6⁵)⁴ = 6²⁰
(vi) \(\large [(\frac {6}{7})⁵]²\)
Solution:
\(\large [(\frac {6}{7})⁵]²\)
= \(\large (\frac {6}{7})⁵ˣ²\) …[∵ (aᵐ)ⁿ = aᵐⁿ]
= \(\large (\frac {6}{7})¹⁰\)
Ans: \(\large [(\frac {6}{7})⁵]²\) = \(\large (\frac {6}{7})¹⁰\)
(vii) \(\large [(\frac {2}{3})⁻⁴]⁵\)
Solution:
\(\large [(\frac {2}{3})⁻⁴]⁵\)
= \(\large (\frac {2}{3})⁻⁴ˣ⁵\) …[∵ (aᵐ)ⁿ = aᵐⁿ]
= \(\large (\frac {2}{3})⁻²⁰\)
Ans: \(\large [(\frac {2}{3})⁻⁴]⁵\) = \(\large (\frac {2}{3})⁻²⁰\)
(viii) \(\large [(\frac {5}{8})³]⁻²\)
Solution:
\(\large [(\frac {5}{8})³]⁻²\)
= \(\large [(\frac {5}{8})³ˣ⁻²\) …[∵ (aᵐ)ⁿ = aᵐⁿ]
= \(\large [(\frac {5}{8})⁻⁶\)
Ans: \(\large (\frac {5}{8})³]⁻²\) = \(\large [(\frac {5}{8})⁻⁶\)
(ix) \(\large [(\frac {3}{4})⁶]¹\)
Solution:
\(\large [(\frac {3}{4})⁶]¹\)
= \(\large (\frac {3}{4})⁶ˣ¹\) …[∵ (aᵐ)ⁿ = aᵐⁿ]
= \(\large [(\frac {3}{4})⁶\)
Ans: \(\large [(\frac {3}{4})⁶]¹\) = \(\large [(\frac {3}{4})⁶\)
(x) \(\large [(\frac {2}{3})⁻³]²\)
Solution:
\(\large [(\frac {2}{3})⁻³]²\)
= \(\large [(\frac {2}{3})⁻³ˣ²\) …[∵ (aᵐ)ⁿ = aᵐⁿ]
= \(\large [(\frac {2}{3})⁻⁶\)
Ans: \(\large [(\frac {2}{3})⁻³]²\) = \(\large [(\frac {2}{3})⁻⁶\)
2. Write the following numbers using positive indices:
(i) \(\large \frac {2}{3})\)⁻²
Solution:
\(\large \frac {2}{3})\)⁻²
= \(\large \frac {3}{2})\)² …[∵ \(\large \frac {a}{b})⁻ᵐ\) = \(\large \frac {b}{a})ᵐ\)]
Ans: \(\large \frac {2}{3})\)⁻² = \(\large \frac {3}{2})\)²
(ii) \(\large \frac {11}{3})\)⁻⁵
Solution:
\(\large \frac {11}{3})\)⁻⁵
= \(\large \frac {3}{11})\)⁵ …[∵ \(\large \frac {a}{b})⁻ᵐ\) = \(\large \frac {b}{a})ᵐ\)]
Ans: \(\large \frac {11}{3})\)⁻⁵ = \(\large \frac {3}{11})\)⁵
(iii) \(\large \frac {1}{6})\)⁻³
Solution:
\(\large \frac {1}{6})\)⁻³
= \(\large \frac {6}{1})\)³ …[∵ \(\large \frac {a}{b})⁻ᵐ\) = \(\large \frac {b}{a})ᵐ\)]
= 6³
Ans: \(\large \frac {1}{6})\)⁻³ = 6³
(iv) (y)⁻⁴
Solution:
(y)⁻⁴
= \(\large \frac {1}{y})\)⁴ …[∵ \(\large \frac {a}{b})⁻ᵐ\) = \(\large \frac {b}{a})ᵐ\)]
Ans: (y)⁻⁴ = \(\large \frac {1}{y})\)⁴
Practice Set 30
Find the square root.
(i) 625
Solution:
∴ 625 = 5 × 5 × 5 × 5
∴ \(\sqrt{625}\) = 5 × 5 = 25
(ii) 1225
Solution:
∴ 1225 = 5 × 5 × 7 × 7
∴ \(\sqrt{1225}\) = 5 × 7 = 35
(iii) 289
Solution:
∴ 289 = 17 × 17
∴ \(\sqrt{289}\) = 17
(iv) 4096
Solution:
∴ 4096 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
∴ \(\sqrt{4096}\) = 2 × 2 × 2 × 2 × 2 × 2 = 64
(v) 1089
Solution:
∴ 1089 = 3 × 3 × 11 × 11
∴ \(\sqrt{1089}\) = 3 × 11 = 33
