Chapter 5 – Operations on Rational Numbers
Practice Set 22
1. Carry out the following additions of rational numbers.
(i) \(\large \frac {5}{36}\) + \(\large \frac {6}{42}\)
Solution:
\(\large \frac {5}{36}\) + \(\large \frac {6}{42}\)
= \(\large \frac {5\,×\,7}{36\,×\,7}\) + \(\large \frac {6\,×\,6}{42\,×\,6}\)
= \(\large \frac {35}{252}\) + \(\large \frac {36}{242}\)
= \(\large \frac {35\,+\,36}{252}\)
= \(\large \frac {71}{252}\)
∴ \(\large \frac {5}{36}\) + \(\large \frac {6}{42}\) = \(\large \frac {71}{252}\)
(ii) 1 \(\large \frac {2}{3}\) + 2 \(\large \frac {4}{5}\)
Solution:
1 \(\large \frac {2}{3}\) + 2 \(\large \frac {4}{5}\)
= \(\large \frac {1\,×\,3\,+\,2}{3}\) + \(\large \frac {2\,×\,5\,+\,4}{5}\)
= \(\large \frac {5}{3}\) + \(\large \frac {14}{5}\)
= \(\large \frac {5\,×\,5}{3\,×\,5}\) + \(\large \frac {14\,×\,3}{5\,×\,3}\)
= \(\large \frac {25}{15}\) + \(\large \frac {42}{15}\)
= \(\large \frac {25\,+\,42}{15}\)
∴ 1 \(\large \frac {2}{3}\) + 2 \(\large \frac {4}{5}\) = \(\large \frac {25\,+\,42}{15}\)
(iii) \(\large \frac {11}{17}\) + \(\large \frac {13}{19}\)
Solution:
\(\large \frac {11}{17}\) + \(\large \frac {13}{19}\)
= \(\large \frac {11\,×\,19}{17\,×\,19}\) + \(\large \frac {13\,×\,17}{19\,×\,17}\)
= \(\large \frac {209}{323}\) + \(\large \frac {221}{323}\)
= \(\large \frac {209\,+\,221}{323}\)
= \(\large \frac {430}{323}\)
∴ \(\large \frac {11}{17}\) + \(\large \frac {13}{19}\) = \(\large \frac {430}{323}\)
(iv) 2 \(\large \frac {3}{11}\) + 1 \(\large \frac {3}{77}\)
Solution:
2 \(\large \frac {3}{11}\) + 1 \(\large \frac {3}{77}\)
= \(\large \frac {2\,×\,11\,+\,3}{11}\) + \(\large \frac {1\,×\,77\,+\,3}{77}\)
= \(\large \frac {25}{11}\) + \(\large \frac {80}{77}\)
= \(\large \frac {25\,×\,7}{11\,×\,7}\) + \(\large \frac {80}{77}\)
= \(\large \frac {175}{77}\) + \(\large \frac {80}{77}\)
= \(\large \frac {175\,+\,80}{77}\)
= \(\large \frac {255}{77}\)
∴ 2 \(\large \frac {3}{11}\) + 1 \(\large \frac {3}{77}\) = \(\large \frac {255}{77}\)
2. Carry out the following subtractions involving rational numbers.
(i) \(\large \frac {7}{11}\) – \(\large \frac {3}{7}\)
Solution:
\(\large \frac {7}{11}\) – \(\large \frac {3}{7}\)
= \(\large \frac {7\,×\,7}{11\,×\,7}\) – \(\large \frac {3\,×\,11}{7\,×\,11}\)
= \(\large \frac {49}{77}\) – \(\large \frac {33}{77}\)
= \(\large \frac {49\,–\,33}{77}\)
= \(\large \frac {16}{323}\)
∴ \(\large \frac {7}{11}\) – \(\large \frac {3}{7}\) = \(\large \frac {16}{323}\)
(ii) \(\large \frac {13}{36}\) – \(\large \frac {2}{40}\)
Solution:
\(\large \frac {13}{36}\) – \(\large \frac {2}{40}\)
= \(\large \frac {13}{36}\) – \(\large \frac {2\,×\,1}{2\,×\,20}\)
= \(\large \frac {13}{36}\) – \(\large \frac {1}{20}\)
= \(\large \frac {13}{36}\) – \(\large \frac {1}{20}\)
= \(\large \frac {13\,×\,5}{36\,×\,5}\) – \(\large \frac {1\,×\,9}{20\,×\,9}\)
= \(\large \frac {65}{180}\) – \(\large \frac {9}{180}\)
= \(\large \frac {65\,–\,9}{180}\)
= \(\large \frac {4\,×\,14}{4\,×\,45}\)
= \(\large \frac {14}{45}\)
∴ \(\large \frac {13}{36}\) – \(\large \frac {2}{40}\) = \(\large \frac {14}{45}\)
(iii) 1 \(\large \frac {2}{3}\) – 3 \(\large \frac {5}{6}\)
Solution:
1 \(\large \frac {2}{3}\) – 3 \(\large \frac {5}{6}\)
= \(\large \frac {1\,×\,3\,+\,2}{3}\) – \(\large \frac {3\,×\,6\,+\,5}{6}\)
= \(\large \frac {5}{3}\) – \(\large \frac {23}{6}\)
= \(\large \frac {5\,×\,2}{3\,×\,2}\) – \(\large \frac {23}{6}\)
= \(\large \frac {10}{6}\) – \(\large \frac {23}{6}\)
= \(\large \frac {–\,13}{6}\)
∴ 1 \(\large \frac {2}{3}\) – 3 \(\large \frac {5}{6}\) = \(\large \frac {–\,13}{6}\)
(iv) 4 \(\large \frac {1}{2}\) – 3 \(\large \frac {1}{3}\)
Solution:
4 \(\large \frac {1}{2}\) – 3 \(\large \frac {1}{3}\)
= \(\large \frac {4\,×\,2\,+\,1}{2}\) – \(\large \frac {3\,×\,3\,+\,1}{3}\)
= \(\large \frac {9}{2}\) – \(\large \frac {10}{3}\)
= \(\large \frac {9\,×\,3}{2\,×\,3}\) – \(\large \frac {10\,×\,2}{3\,×\,2}\)
= \(\large \frac {27}{6}\) – \(\large \frac {20}{6}\)
= \(\large \frac {27\,–\,20}{6}\)
= \(\large \frac {7}{6}\)
∴ 4 \(\large \frac {1}{2}\) – 3 \(\large \frac {1}{3}\) = \(\large \frac {7}{6}\)
3. Multiply the following rational numbers.
(i) \(\large \frac {3}{11}\) × \(\large \frac {2}{5}\)
Solution:
\(\large \frac {3}{11}\) × \(\large \frac {2}{5}\)
= \(\large \frac {3}{11}\) × \(\large \frac {2}{5}\)
= \(\large \frac {3\,×\,2}{11\,×\,5}\)
= \(\large \frac {6}{55}\)
∴ \(\large \frac {3}{11}\) × \(\large \frac {2}{5}\) = \(\large \frac {6}{55}\)
(ii) \(\large \frac {12}{5}\) × \(\large \frac {4}{15}\)
Solution:
\(\large \frac {12}{5}\) × \(\large \frac {4}{15}\)
= \(\large \frac {12\,×\,4}{5\,×\,15}\)
= \(\large \frac {48}{75}\)
= \(\large \frac {16\,×\,3}{25\,×\,3}\)
= \(\large \frac {16}{25}\)
∴ \(\large \frac {12}{5}\) × \(\large \frac {4}{15}\) = \(\large \frac {16}{25}\)
(iii) \(\large \frac {–\,8}{9}\) × \(\large \frac {3}{4}\)
Solution:
\(\large \frac {–\,8}{9}\) × \(\large \frac {3}{4}\)
= \(\large \frac {–\,8\,×\,3}{9\,×\,4}\)
= \(\large \frac {–\,24}{36}\)
= \(\large \frac {–\,2\,×\,12}{3\,×\,12}\)
= \(\large \frac {–\,2}{3}\)
∴ \(\large \frac {–\,8}{9}\) × \(\large \frac {3}{4}\) = \(\large \frac {–\,2}{3}\)
(iv) \(\large \frac {0}{6}\) × \(\large \frac {3}{4}\)
Solution:
\(\large \frac {0}{6}\) × \(\large \frac {3}{4}\)
= 0 × \(\large \frac {3}{4}\)
= 0
∴ \(\large \frac {0}{6}\) × \(\large \frac {3}{4}\) = 0
4. Write the multiplicative inverse.
(i) \(\large \frac {2}{5}\)
Solution:
Multiplicative inverse of \(\large \frac {2}{5}\) is \(\large \frac {5}{2}\)
(ii) \(\large \frac {–\,3}{8}\)
Solution:
Multiplicative inverse of \(\large \frac {–\,3}{8}\) is \(\large \frac {–\,8}{3}\)
(iii) \(\large \frac {–17}{39}\)
Solution:
Multiplicative inverse of \(\large \frac {–17}{39}\) is \(\large \frac {–39}{17}\)
(iv) 7
Solution:
Multiplicative inverse of 7 is \(\large \frac {1}{7}\)
(v) – 7 \(\large \frac {1}{3}\)
Solution:
– 7 \(\large \frac {1}{3}\)
= – \(\large \frac {7\,×\,3\,+\,1}{3}\)
= – \(\large \frac {22}{3}\)
∴ Multiplicative inverse of – \(\large \frac {22}{3}\) is – \(\large \frac {3}{22}\)
5. Carry out the divisions of rational numbers.
(i) \(\large \frac {40}{12}\) ÷ \(\large \frac {10}{4}\)
Solution:
\(\large \frac {40}{12}\) ÷ \(\large \frac {10}{4}\)
= \(\large \frac {40}{12}\) × \(\large \frac {4}{10}\)
= \(\large \frac {4}{3}\)
∴ \(\large \frac {40}{12}\) ÷ \(\large \frac {10}{4}\) = \(\large \frac {4}{3}\)
(ii) \(\large \frac {–\,10}{11}\) ÷ \(\large \frac {–\,11}{10}\)
Solution:
\(\large \frac {–\,10}{11}\) ÷ \(\large \frac {–\,11}{10}\)
= \(\large \frac {–\,10}{11}\) × \(\large \frac {–\,10}{11}\)
= \(\large \frac {100}{121}\)
∴ \(\large \frac {–\,10}{11}\) ÷ \(\large \frac {–\,11}{10}\) = \(\large \frac {100}{121}\)
(iii) \(\large \frac {–\,7}{8}\) ÷ \(\large \frac {–\,3}{6}\)
Solution:
\(\large \frac {–\,7}{8}\) ÷ \(\large \frac {–\,3}{6}\)
= \(\large \frac {–\,7}{8}\) × \(\large \frac {–\,6}{3}\)
= \(\large \frac {7}{4}\)
∴ \(\large \frac {–\,7}{8}\) ÷ \(\large \frac {–\,3}{6}\) = \(\large \frac {7}{4}\)
(iv) \(\large \frac {2}{3}\) ÷ (– 4)
Solution:
\(\large \frac {2}{3}\) ÷ (– 4)
= \(\large \frac {2}{3}\) ÷ \(\large \frac {1}{–\,4}\)
= \(\large \frac {–\,1}{6}\)
∴ \(\large \frac {2}{3}\) ÷ (– 4) = \(\large \frac {–\,1}{6}\)
(v) 2 \(\large \frac {1}{5}\) ÷ 5 \(\large \frac {3}{6}\)
Solution:
2 \(\large \frac {1}{5}\) ÷ 5 \(\large \frac {3}{6}\)
= \(\large \frac {2\,×\,5\,+\,1}{5}\) ÷ \(\large \frac {5\,×\,6\,+\,3}{6}\)
= \(\large \frac {11}{5}\) ÷ \(\large \frac {33}{6}\)
= \(\large \frac {11}{5}\) × \(\large \frac {6}{33}\)
= \(\large \frac {11\,×\,6}{5\,×\,33}\)
= \(\large \frac {2}{5}\)
∴ 2 \(\large \frac {1}{5}\) ÷ 5 \(\large \frac {3}{6}\) = \(\large \frac {2}{5}\)
(vi) \(\large \frac {–\,5}{13}\) ÷ \(\large \frac {7}{26}\)
Solution:
\(\large \frac {–\,5}{13}\) ÷ \(\large \frac {7}{26}\)
= \(\large \frac {–\,5}{13}\) × \(\large \frac {26}{7}\)
= \(\large \frac {–\,5\,×\,26}{13\,×\,7}\)
= \(\large \frac {–\,5\,×\,2}{7}\)
= \(\large \frac {–\,10}{7}\)
∴ \(\large \frac {–\,5}{13}\) ÷ \(\large \frac {7}{26}\) = \(\large \frac {–\,10}{7}\)
(vii) \(\large \frac {9}{11}\) ÷ (– 8)
Solution:
\(\large \frac {9}{11}\) ÷ (– 8)
= \(\large \frac {9}{11}\) × \(\large \frac {1}{–\,8}\)
= \(\large \frac {9\,×\,1}{11\,×\,–\,8}\)
= \(\large \frac {9}{–\,88}\)
= \(\large \frac {–\,9}{88}\)
∴ \(\large \frac {9}{11}\) ÷ (– 8) = \(\large \frac {–\,9}{88}\)
(viii) 5 ÷ \(\large \frac {2}{5}\)
Solution:
5 ÷ \(\large \frac {2}{5}\)
= 5 × \(\large \frac {5}{3}\)
= \(\large \frac {5\,×\,5}{3}\)
= \(\large \frac {25}{3}\)
∴ 5 ÷ \(\large \frac {2}{5}\) = \(\large \frac {25}{3}\)
Practice Set 23
(i) \(\large \frac {2}{7}\), \(\large \frac {6}{7}\)
Solution:
2 < 3 < 4 < 5 < 6
∴ \(\large \frac {2}{7}\) < \(\large \frac {3}{7}\) < \(\large \frac {4}{7}\) < \(\large \frac {5}{7}\) < \(\large \frac {6}{7}\)
∴ The three rational numbers lying between \(\large \frac {2}{7}\) and \(\large \frac {6}{7}\) are \(\large \frac {3}{7}\), \(\large \frac {4}{7}\), \(\large \frac {5}{7}\)
(ii) \(\large \frac {4}{5}\), \(\large \frac {2}{3}\)
Solution:
\(\large \frac {4}{5}\), \(\large \frac {2}{3}\)
= \(\large \frac {4\,×\,6}{5\,×\,6}\), \(\large \frac {2\,×\,10}{3\,×\,10}\)
= \(\large \frac {24}{30}\), \(\large \frac {20}{30}\)
20 < 21 < 22 < 23 < 24
∴ \(\large \frac {20}{30}\) < \(\large \frac {21}{30}\) < \(\large \frac {22}{30}\) < \(\large \frac {23}{30}\) < \(\large \frac {24}{30}\)
∴ \(\large \frac {4}{5}\) < \(\large \frac {21}{30}\) < \(\large \frac {22}{30}\) < \(\large \frac {23}{30}\) < \(\large \frac {2}{3}\)
∴ The three rational numbers lying between \(\large \frac {4}{5}\) and \(\large \frac {2}{3}\) are \(\large \frac {21}{30}\), \(\large \frac {22}{30}\)
(iii) – \(\large \frac {2}{3}\), \(\large \frac {4}{5}\)
Solution:
– \(\large \frac {2}{3}\), \(\large \frac {4}{5}\)
= – \(\large \frac {2\,×\,5}{3\,×\,5}\), \(\large \frac {4\,×\,3}{5\,×\,3}\)
= – \(\large \frac {10}{15}\), \(\large \frac {12}{15}\)
– 10 < –9 < 0 < 9 < 12
∴ – \(\large \frac {10}{15}\) < – \(\large \frac {9}{15}\) < 0 < – \(\large \frac {9}{15}\) < \(\large \frac {12}{15}\)
∴ – \(\large \frac {2}{3}\) < – \(\large \frac {9}{15}\) < 0 < \(\large \frac {9}{15}\) < \(\large \frac {4}{5}\)
∴ The three rational numbers lying between – \(\large \frac {2}{3}\) and \(\large \frac {4}{5}\) are – \(\large \frac {9}{15}\), 0 and \(\large \frac {9}{15}\).
(iv) \(\large \frac {7}{9}\), – \(\large \frac {5}{9}\)
Solution:
– 5 < – 3 < 0 < 4 < 7
∴ – \(\large \frac {5}{9}\) < – \(\large \frac {3}{9}\) < 0 < \(\large \frac {4}{9}\) < \(\large \frac {7}{9}\)
∴ The three rational numbers lying between \(\large \frac {7}{9}\) and – \(\large \frac {5}{9}\) are – \(\large \frac {3}{9}\), 0 and \(\large \frac {4}{9}\).
(v) \(\large \frac {–\,3}{4}\), \(\large \frac {+\,5}{4}\)
Solution:
– 3 < – 1 < 1 < 3 < 5
∴ \(\large \frac {–\,3}{4}\) < \(\large \frac {–\,1}{4}\) < \(\large \frac {1}{4}\) < \(\large \frac {3}{4}\) < \(\large \frac {5}{4}\)
∴ The three rational numbers lying between \(\large \frac {–\,3}{4}\) and – \(\large \frac {5}{4}\) are \(\large \frac {–\,1}{4}\), \(\large \frac {1}{4}\) and \(\large \frac {3}{4}\).
(vi) \(\large \frac {7}{8}\), \(\large \frac {–\,5}{3}\)
Solution:
\(\large \frac {7}{8}\), \(\large \frac {–\,5}{3}\)
= \(\large \frac {7\,×\,3}{8\,×\,3}\), \(\large \frac {–\,5\,×\,8}{3\,×\,8}\)
= \(\large \frac {21}{24}\), \(\large \frac {–\,40}{24}\)
– 40 < – 30 < – 20 < 7 < 21
∴ \(\large \frac {–\,40}{24}\) < \(\large \frac {–\,30}{24}\) < \(\large \frac {–\,20}{24}\) < \(\large \frac {7}{24}\) < \(\large \frac {21}{24}\)
∴ \(\large \frac {–\,5}{3}\) < \(\large \frac {–\,30}{24}\) < \(\large \frac {–\,20}{24}\) < \(\large \frac {7}{24}\) < \(\large \frac {7}{8}\)
∴ The three rational numbers lying between \(\large \frac {7}{8}\), and \(\large \frac {–\,30}{24}\), \(\large \frac {–\,20}{24}\) and \(\large \frac {7}{24}\).
(vii) \(\large \frac {5}{7}\), \(\large \frac {11}{7}\)
Solution:
5 < 6 < 8 < 10 < 11
∴ \(\large \frac {5}{7}\) < \(\large \frac {6}{7}\) < \(\large \frac {8}{7}\) < \(\large \frac {10}{7}\) < \(\large \frac {11}{7}\)
∴ The three rational numbers lying between \(\large \frac {5}{7}\) and \(\large \frac {11}{7}\) are \(\large \frac {6}{7}\), \(\large \frac {8}{7}\) and \(\large \frac {10}{7}\).
(viii) 0, \(\large \frac {–\,3}{4}\)
Solution:
0, \(\large \frac {–\,3}{4}\)
= \(\large \frac {0\,×\,8}{1\,×\,8}\), \(\large \frac {–\,3\,×\,2}{4\,×\,2}\)
= \(\large \frac {0}{8}\), \(\large \frac {–\,6}{8}\)
∴ – 6 < – 5 < – 4 < – 1 < 0
∴ \(\large \frac {–\,6}{8}\) < \(\large \frac {–\,5}{8}\) < \(\large \frac {–\,3}{8}\) < \(\large \frac {–\,1}{8}\) < \(\large \frac {0}{8}\)
∴ The three rational numbers lying between 0 and \(\large \frac {–\,3}{4}\) are \(\large \frac {–\,5}{8}\), \(\large \frac {–\,3}{8}\) and \(\large \frac {–\,1}{8}\).
Practice set 24
Write the following rational numbers in decimal form.
(i) \(\large \frac {13}{4}\)
Solution:
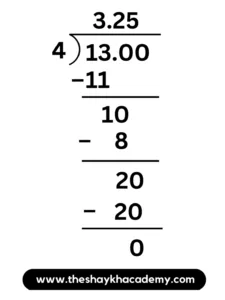
∴ \(\large \frac {13}{4}\) = 3.25
(ii) \(\large \frac {–\,7}{8}\)
Solution:
\(\large \frac {–\,7}{8}\)
= (– 1)\(\large \frac {7}{8}\)
∴ \(\large \frac {–\,7}{8}\) = – 0.875
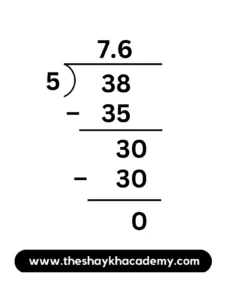
(iii) 7 \(\large \frac {3}{5}\)
Solution:
7 \(\large \frac {3}{5}\)
= \(\large \frac {7\,×\,5\,+\,3}{5}\)
= \(\large \frac {38}{5}\)

∴ 7 \(\large \frac {3}{5}\) = 7.6
(iv) \(\large \frac {5}{12}\)
Solution:

∴ \(\large \frac {5}{12}\) = \(0.41\overset{\boldsymbol\cdot}6\)
(v) \(\large \frac {22}{7}\)
Solution:

∴ \(\large \frac {22}{7}\) = \(3.\overset{\_\_\_\_\_\_\_}{142857}\)
(vi) \(\large \frac {4}{3}\)
Solution:

∴ \(\large \frac {4}{3}\) = \(1.\overset{\boldsymbol\cdot}3\)
(vii) \(\large \frac {7}{9}\)
Solution:
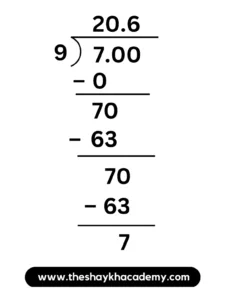
∴ \(\large \frac {7}{9}\) = \(0.\overset{\boldsymbol\cdot}7\)
Practice set 25
Simplify the following expressions.
1. 50 × 5 ÷ 2 + 24
Solution:
50 × 5 ÷ 2 + 24
= 250 ÷ 2 + 24
= 125 + 24
= 149
∴ 50 × 5 ÷ 2 + 24 = 149
2. (13 × 4) ÷ 2 – 26
Solution:
(13 × 4) ÷ 2 – 26
= 52 ÷ 2 – 26
= 26 – 26
= 0
∴ (13 × 4) ÷ 2 – 26 = 0
3. 140 ÷ [(– 11) × (– 3) – (– 42) ÷ 14 – 1)]
Solution:
140 ÷ [(– 11) × (– 3) – (– 42) ÷ 14 – 1)]
= 140 ÷ [33 + 42 ÷ 14 – 1]
= 140 ÷ [33 + 3 – 1]
= 140 ÷ 35
= 4
∴ 140 ÷ [(– 11) × (– 3) – (– 42) ÷ 14 – 1)] = 4
4. {(220 – 140) + [10 × 9 + (– 2 × 5)]} – 100
Solution:
{(220 – 140) + [10 × 9 + (– 2 × 5)]} – 100
= {80 + [90 – 10]} – 100
= {80 + 80} – 100
= 160 – 100
= 60
∴ {(220 – 140) + [10 × 9 + (– 2 × 5)]} – 100 = 60
5. \(\large \frac {3}{5}\) + \(\large \frac {3}{8}\) ÷ \(\large \frac {6}{4}\)
Solution:
\(\large \frac {3}{5}\) + \(\large \frac {3}{8}\) ÷\(\large \frac {6}{4}\)
= \(\large \frac {3}{5}\) + \(\large \frac {3}{8}\) × \(\large \frac {4}{6}\)
= \(\large \frac {3}{5}\) + \(\large \frac {1}{4}\)
= \(\large \frac {3\,×\,4}{5\,×\,4}\) + \(\large \frac {1\,×\,5}{4\,×\,5}\)
= \(\large \frac {12}{20}\) + \(\large \frac {5}{20}\)
= \(\large \frac {12\,+\,5}{20}\)
= \(\large \frac {17}{20}\)
∴ \(\large \frac {3}{5}\) + \(\large \frac {3}{8}\) ÷ \(\large \frac {6}{4}\) = \(\large \frac {17}{20}\)
