Chapter 12 - Perimeter and Area
Practice set 44
1. If the length and breadth of a rectangle are doubled, how many times the perimeter of the old rectangle will that of the new rectangle be?
Given:
Length and breadth of a rectangle are doubled
To find:
The number of times the perimeter of the old rectangle is that of the new rectangle
Solution:
Let the length of the old rectangle be l and breadth be b.
∴ Perimeter of old rectangle = 2(l + b)
Length and breadth of the rectangle is doubled …[Given]
∴ Length of new rectangle = 2l
Breadth of new rectangle = 2b
∴ Perimeter of new rectangle = 2(2l + 2b)
∴ Perimeter of new rectangle = 2 × 2 (l + b)
i.e. Perimeter of new rectangle = 2 × Perimeter of old rectangle
Ans: The perimeter of the new rectangle will be twice the perimeter of the old rectangle.
2. If the side of a square is tripled, how many times the perimeter of the first square will that of the new square be?
Given:
Side of a square is tripled
To find:
The number of times the perimeter of the first square is that of the new square
Solution:
Let the length of the square be a.
∴ Perimeter of first square = 4 × side
∴ Perimeter of first square = 4 × a
∴ Perimeter of first square = 4a
Side of the square is tripled
∴ Side of new square = 3 × a
∴ Side of new square = 3a
Perimeter of new square = 4 × side
∴ Perimeter of new square = 4 × 3a
∴ Perimeter of new square = 3 × 4a
i.e. Perimeter of new square = 3 × Perimeter of first square.
Ans: The perimeter of the new square will be three times the perimeter of the original square.
3. Given alongside is the diagram of a playground. It shows the length of its sides. Find the perimeter of the playground.
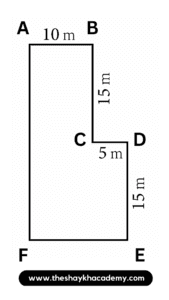
Given:
Refer diagram,
AB = 10 m
BC = 15 m
CD = 5 m
DE = 15 m
To find:
Perimeter of the playground.
Solution:
Side AF = side BC + side DE
∴ Side AF = 15 + 15
∴ Side AF = 30 m
Side FE = side AB + side CD
∴ Side FE = 10 + 5
∴ Side FE = 15 m
Perimeter of the playground = side AB + side BC + side CD + side DE + side FE + side AF
∴ Perimeter of the playground = 10 + 15 + 5 + 15 + 15 + 30
∴ Perimeter of the playground = 90 m
Ans: The perimeter of the playground is 90 m.
4. As shown in the figure, four napkins all of the same size were made from a square piece of cloth of length 1 m. What length of lace will be required to trim all four sides of all the napkins?

Given:
Side of the square piece of cloth = 1 m
To find:
Length of lace will be required to trim all four sides of all the napkins
Solution:
Side of the square piece of cloth
Each side consists of 2 napkins
∴ Side of each napkin = \(\large \frac {1}{2}\) × 1 m
∴ Side of each napkin = 0.5 m
Length of lace that will be required for 1 napkin = Perimeter of the napkin
∴ Perimeter of the napkin = 4 × side
∴ Perimeter of the napkin = 4 × 0.5
∴ Perimeter of the napkin = 2 m
There are altogether 4 napkins
∴ Perimeter of 4 napkins = 4 × 2
∴ Perimeter of 4 napkins = 8 m
Ans: 8 metre long lace will be required to trim all four napkins.
Practice set 45
1. If the side of a square is 12 cm, find its area.
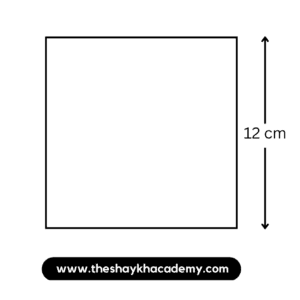
Given:
Side of a square = 12 cm
To find:
Area of the square
Solution:
Area of a square = (side)²
∴ Area of a square = (12)²
∴ Area of a square = 144 sq. cm.
Ans: The area of the square is 144 sq. cm.
2. If the length of a rectangle is 15 cm and breadth is 5 cm, find its area.
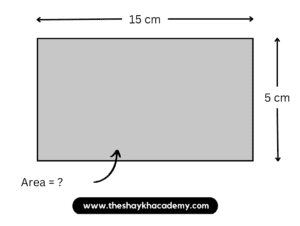
Given:
Length of a rectangle = 15 cm
Breadth of the rectangle = 5 cm
To find:
Area of rectangle
Solution:
Area of a rectangle = length × breadth
∴ Area of a rectangle = 15 × 5
∴ Area of a rectangle = 75 sq. cm.
Ans: The area of the rectangle is 75 sq. cm.
3. The area of a rectangle is 102 sqcm. If its length is 17 cm, what is its perimeter?
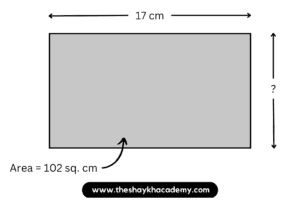
Given:
Area of a rectangle = 102 sq.cm
Length of the rectangle = 17 cm
To find:
Perimeter of the rectangle
Solution:
Area of a rectangle = length × breadth
∴ 102 = 17 × breadth
∴ breadth = \(\large \frac {102}{17}\)
∴ breadth = 6 cm
Perimeter of the rectangle = 2 (length + breadth)
∴ Perimeter of the rectangle = 2 (17 + 6)
∴ Perimeter of the rectangle = 2 × 23
∴ Perimeter of the rectangle = 46 cm
Ans: Perimeter of the rectangle is 46 cm.
4*. If the side of a square is tripled, how many times will its area be as compared to the area of the original square?
Given:
Side of a square is tripled
To find:
The number of times the area of the new square is that of the original square
Solution:
Let the side of the square be a
∴ Area of a square = (side)²
∴ Area of a square = a²
New side of the square = 3 × a
∴ New side of the square = 3a
Area of the new square = (3a)²
∴ Area of the new square = 9a²
∴ Area of the new square = 9 × area of original square
Ans: If the side of a square is tripled, its area will become 9 times the area of the original square.
Practice set 46
1. A page of a calendar is 45 cm long and 26 cm wide. What is its area?
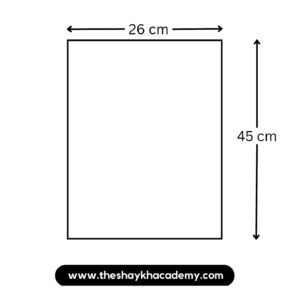
Given:
Length of page of the calendar = 45 cm
Breadth of page of the calendar = 26 cm
To find:
Area of the page of the calendar
Solution:
Area of page of the calendar = length × breadth
∴ Area of page of the calendar = 45 × 26
∴ Area of page of the calendar = 1170 sq. cm.
Ans: The area of the page of the calendar is 1170 sq.cm
2. What is the area of a triangle with base 4.8 cm and height 3.6 cm?

Given:
Base of the triangle = 4.8 cm
Height of the triangle = 3.6 cm
To find:
Area of the triangle
Solution:
Area of triangle = 12 × base × height
∴ Area of triangle = 12 × 4.8 × 3.6
∴ Area of triangle = 12 × 17.28
∴ Area of triangle = 8.64 sq. cm.
Ans: The area of the triangle is 8.64 sq.cm
3. What is the value of a rectangular plot of land 75.5 m long and 30.5 m broad at the rate of 1000 rupees per square metre?
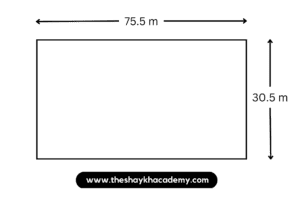
Given:
Length of the rectangular plot = 75.5 m
Breadth of the rectangular plot = 30.5 m
Rate per sq.m = ₹ 1000
To find:
Value of the rectangular plot
Solution:
Area of the rectangular plot = length × breadth
∴ Area of the rectangular plot = 75.5 × 30.5
∴ Area of the rectangular plot = 2302.75 sq. m.
Value of the plot = area of the plot × rate per square metre = 2302.75 × 1000
∴ Value of the plot = 2302.75 × 1000
∴ Value of the plot = Rs 230275
Ans: The value of the plot is Rs 23,02,750.
4. A rectangular hall is 12 m long and 6 m broad. Its flooring is to be made of square tiles of side 30 cm. How many tiles will fit in the entire hall? How many would be required if tiles of side 15 cm were used?
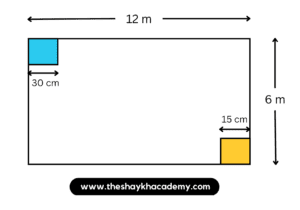
Given:
Length of the rectangular hall = 12 m
Breadth of the rectangular hall = 6 m
Side of square tile = 30 cm
To find:
No of tile required to fit in the rectangular hall
Solution:
Area of the rectangular hall = length × breadth
∴ Area of the rectangular hall = 12 × 6
∴ Area of the rectangular hall = 72 sq. m.
Side of the square shaped tile = 30 cm = 0.3 m
∴ Area of the tile = (side)²
∴ Area of the tile = (0.3)²
∴ Area of the tile = 0.09 sq.m
Number of tiles required = \(\large \frac {\text Area of the hall}{\text Area of each tile}\)
∴ Number of tiles required = \(\large \frac {72}{0.09}\)
∴ Number of tiles required = \(\large \frac {72\,×\, 100}{9}\)
∴ Number of tiles required = 800
Now,
Side of the square shaped tile = 15 cm = 0.15 m
∴ Area of the tile = (side)²
∴ Area of the tile = (0.15)²
∴ Area of the tile = 0.0225 sq.m
∴ Number of tiles required = \(\large \frac {\text Area of the hall}{\text Area of each tile}\)
∴ Number of tiles required = \(\large \frac {72}{0.0225}\)
∴ Number of tiles required = \(\large \frac {72\,×\, 10000}{225}\)
∴ Number of tiles required = 3200
Ans: 800 square shaped tiles of 30 cm side will be required and 3200 square shaped tiles of 15 cm side will be required.
5. Find the perimeter and area of a garden with measures as shown in the figure alongside.
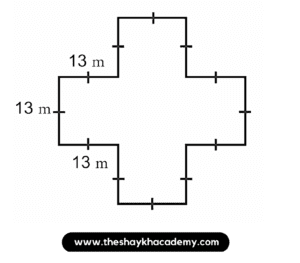
Given:
The boundary of the garden is made of 12 sides each of length 13 m
To find:
The perimeter and area of the garden
Solution:
Perimeter of the garden = Sum of the lengths of all sides
∴ Perimeter of the garden = 12 (13)
∴ Perimeter of the garden = 156 m
The garden in the given figure can be divided into 5 squares each of side 13 m.
∴ Area of the garden = 5 × Area of each square part
∴ Area of the garden = 5 × (side)²
∴ Area of the garden = 5 × (13)²
∴ Area of the garden = 5 × 169
∴ Area of the garden = 845 sq.m
Ans: The perimeter and area of a garden are 156 m and 845 sq. m. respectively
Practice set 47
1. Find the total surface area of cubes having the following sides.
(i) 3 cm

Given:
Side = 3 cm
To find:
Total surface area of cube
Solution:
Total surface area of cube = 6l²
∴ Total surface area of cube = 6 × 3²
∴ Total surface area of cube = 6 × 9
∴ Total surface area of cube = 54 sq.cm
Ans: Total surface area of cube is 54 sq.cm
(ii) 5 cm
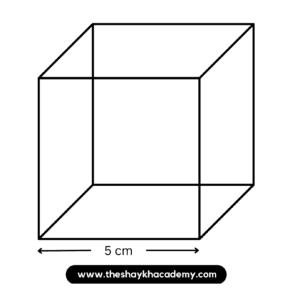
Given:
Side = 5 cm
To find:
Total surface area of the cube
Solution:
Total surface area of the cube = 6l²
∴ Total surface area of the cube = 6 × 5²
∴ Total surface area of the cube = 6 × 25
∴ Total surface area of the cube = 150 sq. m.
Ans: Total surface area of the cube is 150 sq. m.
(iii) 7.2 m

Given:
Side = 7.2 m
To find:
Total surface area of the cube
Solution:
Total surface area of the cube = 6l²
∴ Total surface area of the cube = 6 × 7.2²
∴ Total surface area of the cube = 6 × 51.84
∴ Total surface area of the cube = 311.04 sq. m.
Ans: Total surface area of the cube is 311.04 sq. m.
(iv) 6.8 m

Given:
Side = 6.8 m
To find:
Total surface area of the cube
Solution:
Total surface area of the cube = 6l²
∴ Total surface area of the cube = 6 × 6.8²
∴ Total surface area of the cube = 6 × 46.24
∴ Total surface area of the cube = 277.44 sq. m.
Ans: Total surface area of the cube is 277.44 sq. m.
(v) 5.5 m

Given:
Side = 5.5 m
To find:
Total surface area of cube
Solution:
Total surface area of the cube = 6l²
∴ Total surface area of the cube = 6 × (5.5)²
∴ Total surface area of the cube = 6 × 30.25
∴ Total surface area of the cube = 181.5 sq. m.
Ans: Total surface area of the cube is 181.5 sq. m.
2. Find the total surface area of the cuboids of length, breadth and height as given below:
(i) 12 cm, 10 cm, 5 cm
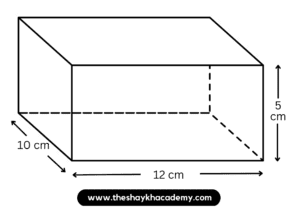
Given:
Length of the cuboid = 12 cm
Breadth of the cuboid = 10 cm
Height of the cuboid = 5 cm
To find:
Total surface area of cuboid
Solution:
Total surface area of cuboid
∴ Total surface area of cuboid = 2 (lb + bh + lh)
∴ Total surface area of cuboid = 2 (12 × 10 + 10 × 5 + 12 × 5)
∴ Total surface area of cuboid = 2 (120 + 50 + 60)
∴ Total surface area of cuboid = 2 × 230
∴ Total surface area of cuboid = 460 sq. cm.
Ans: Total surface area of cuboid is 460 sq. cm.
(ii) 5 cm, 3.5 cm, 1.4 cm
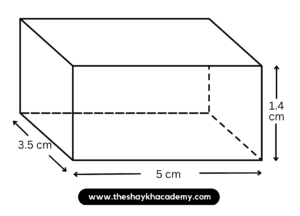
Given:
Length of the cuboid = 5 cm
Breadth of the cuboid = 3.5 cm
Height of the cuboid = 1.4 cm
To find:
Total surface area of cuboid
Solution:
Total surface area of cuboid = 2 (lb + bh + lh)
∴ Total surface area of cuboid = 2 (8 × 5+ 5 × 3.5 + 8 × 3.5)
∴ Total surface area of cuboid = 2(40 + 17.5 + 28)
∴ Total surface area of cuboid = 2 × 85.5
∴ Total surface area of cuboid = 171 sq. m.
Ans: Total surface area of cuboid is 171 sq. m.
(iii) 2.5 m, 2 m, 2.4 m
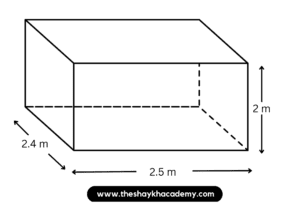
Given:
Length of the cuboid = 2.5 m
Breadth of the cuboid = 2.4 m
Height of the cuboid = 2 m
To find:
Total surface area of cuboid
Solution:
Total surface area of cuboid = 2 (lb + bh + lh)
∴ Total surface area of cuboid = 2(2.5 × 2.4 + 2.4 × 2 + 2.5 × 2)
∴ Total surface area of cuboid = 2 (6 + 4.8 + 5)
∴ Total surface area of cuboid = 2 × 15.8
∴ Total surface area of cuboid = 31.6 sq. m.
Ans: Total surface area of cuboid is 31.6 sq. m.
(iv) 8 m, 5 m, 3.5 m
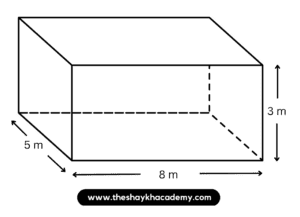
Given:
Length of the cuboid = 8 m
Breadth of the cuboid = 5 m
Height of the cuboid = 3.5 m
To find:
Total surface area of cuboid
Solution:
Total surface area of cuboid = 2 (lb + bh + lh)
∴ Total surface area of cuboid = 2 (8 × 5+ 5 × 3.5 + 8 × 3.5)
∴ Total surface area of cuboid = 2(40 + 17.5 + 28)
∴ Total surface area of cuboid = 2 × 85.5
∴ Total surface area of cuboid = 171 sq. m.
Ans: Total surface area of cuboid is 171 sq. m.
3. A matchbox is 4 cm long, 2.5 cm broad and 1.5 cm in height. Its outer sides are to be covered exactly with craft paper. How much paper will be required to do so?

Given:
Length of the matchbox = 4 cm
Breadth of the matchbox = 2.5 cm
Height of the matchbox = 1.5 cm
To find:
Paper required to cover the box with craft paper
Solution:
Total surface area of the matchbox = 2 (lb + bh + lh)
∴ Total surface area of the matchbox = 2 (4 × 2.5 + 2.5 × 1.5 + 4 × 1.5)
∴ Total surface area of the matchbox = 2 (10 + 3.75 + 6)
∴ Total surface area of the matchbox = 2 × 19.75
∴ Total surface area of the matchbox = 39.5 sq. cm.
Ans: 39.5 sq.cm paper will be required.
4. An open box of length 1.5 m, breadth 1 m, and height 1 m is to be made for use on a trolley for carrying garden waste. How much sheet metal will be required to make this box? The inside and outside surface of the box is to be painted with rust proof paint. At a rate of 150 rupees per sqm, how much will it cost to paint the box?
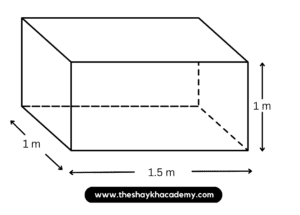
Given:
Length of the box = 1.5 m
Breadth of the box = 1 m
Height of the box = 1 m
Rate of painting per sq. m = ₹150
To find:
Quantity of Metal sheet required to make the box
Solution:
The box is open at the top
∴ Sheet required to make the box = Total surface area of the box – Area of the top
∴ Sheet required to make the box = 2 (lb + bh + lh) – lb
∴ Sheet required to make the box = 2lb + 2bh + 2lh – lb
∴ Sheet required to make the box = lb + 2bh + 2lh
∴ Sheet required to make the box = (1.5 × 1) + (2 × 1 × 1) + (2 × 1.5 × 1)
∴ Sheet required to make the box = 1.5 + 2 + 3
∴ Sheet required to make the box = 6.5 sq. m.
Since, the inside and outside surface of the box are to be painted.
∴ Area to be painted = 2 × Area of the box
∴ Area to be painted = 2 × 6.5
∴ Area to be painted = 13 sq. m.
Total cost of painting = Area to be painted × Rate per sq. m.
∴ Total cost of painting = 13 × 150
∴ Total cost of painting = ₹1950
Ans: 6.5 sq. m. sheet of metal will be required and the cost of painting the box will be ₹1950.
