Chapter 10 - Banks and Simple Interest
Practice Set 40
1. If Rihanna deposits 1500 rupees in the school fund at 9 p.c.p.a for 2 years, what is the total amount she will get?
Given:
P = Rs 1500
R = 9 p.c.p.a
T = 2 years
To find:
Total Amount
Solution:
Total interest = \(\large \frac{P\, ×\, R\, ×\, T}{100} \)
Total interest = \(\large \frac{1500\, ×\, 9\, ×\, 2}{100} \)
Total interest = 15 × 9 × 2
Total interest = Rs 270
Total amount = Principal + Interest
∴ Total amount = 1500 + 270
∴ Total amount = Rs 1770
Ans: Rihanna will get a total amount of Rs 1770.
2. Jethalal took a housing loan of 2,50,000 rupees from a bank at 10 p.c.p.a. for 5 years. What is the yearly interest he must pay and the total amount he returns to the bank?
Given:
P = Rs 250000
R = 10 p.c.p.a.
T = 5 years
To find:
Yearly Interest
Total Amount
Solution:
Total interest = \(\large \frac{P\, ×\, R\, ×\, T}{100} \)
Total interest = \(\large \frac{250000\, ×\, 10\, ×\, 5}{100} \)
Total interest = 2500 × 10 × 5
Total interest = Rs 1,25,000
Yearly interest = \(\large \frac {Total\, interest}{Time} \)
∴ Yearly interest = \(\large \frac{1,25,000}{5} \)
∴ Yearly interest = Rs 25000
Total amount = Principal + Total interest
∴ Total amount = 250000 + 125000
∴ Total amount = Rs 375000
Ans: The yearly interest is Rs 25,000 and Jethalal will have to return Rs 3,75,000 to the bank.
3*. Shrikant deposited 85,000 rupees for 2 ½ years at 7 p.c.p.a. in a savings bank account. What is the total interest he received at the end of the period?
Given:
P = Rs 85000
R = 7 p.c.p.a.
T = 2½ years = 2.5 years
To find:
Total Interest
Solution:
Total interest = \(\large \frac{P\, ×\, R\, ×\, T}{100} \)
Total interest = \(\large \frac{85000\, ×\, 7\, ×\, 2.5}{100} \)
Total interest = \(\large \frac{85000\, ×\, 7\, ×\, 25}{100\, ×\, 10} \)
Total interest = 85 × 7 × 25
Total interest = Rs 14875
Ans: The total interest received by Shrikant at the end of the period is Rs 14875.
4. At a certain rate of interest, the interest after 4 years on 5000 rupees principal is 1200 rupees. What would be the interest on 15000 rupees at the same rate of interest for the same period?
Given:
\( P_1 \) = Rs 5000
\( I_1 \) = Rs 1200
\( T_1 \) = \( T_2 \) = 4 years
\( P_2 \) = Rs 15000
\( R_1 \) = \( R_2 \)
To find:
\( I_2 \)
Solution:
Total interest = \(\large \frac{P × R × T}{100} \)
∴ \( I_1 \) = \(\large \frac{P_1\, ×\, R_1\, ×\, T_1}{100} \)
∴ 1200 = \(\large \frac{5000\, ×\, R_1\, ×\, 4}{100} \)
∴ \(\large \frac{1200\, ×\, 100}{5000\, ×\, 4} \) = \( R_1 \)
∴ \( R_1 \) = \(\large \frac{120000}{20000} \)
∴ \( R_1 \) = 6 years …(i)
And,
∴ \( I_2 \) = \(\large \frac{P_2\, ×\, R_2\, ×\, T_2}{100} \)
∴ \( I_2 \) = \(\large \frac{15000\, ×\, R_2\, ×\, 4}{100} \)
∴ \( I_2 \) = \(\large \frac{60000\, ×\, R_2}{100} \)
∴ \( I_2 \) = 600 × \( R_2 \)
∴ \( R_2 \) = \(\large \frac{I_2}{600} \) years …(ii)
But \( R_1 \) = \( R_2 \)
∴ 6 = \(\large \frac{I_2}{600} \)
∴ \( I_2 \) = 6 × 600
∴ \( I_2 \) = 3600
Ans: The interest received on Rs 15000 is Rs 3600.
5. If Pankaj deposits 1,50,000 rupees in a bank at 10 p.c.p.a. for two years, what is the total amount he will get from the bank?
Given:
P = 150000
R = 10 p.c.p.a.
T = 2 years
To find:
Total Amount
Solution:
Total interest = \(\large \frac{P\, ×\, R\, ×\, T}{100} \)
Total interest = \(\large \frac{150000 \, ×\, 10\, ×\, 2}{100} \)
Total Interest = Rs 30000
Total amount = Principal + Total Interest
∴ Total amount = 150000 + 30000
∴ Total amount = Rs 180000
Ans: Pankaj will receive Rs 180000 from the bank.
Practice Set 41
1. If the interest on 1700 rupees is 340 rupees for 2 years the rate of interest must be ……… .
(i) 12 %
(ii) 15 %
(iii) 4 %
(iv) 10 %
Given:
P = Rs 1700
I = Rs 340
T = 2 years
To find:
Rate of interest
Solution:
Total interest = \(\large \frac{P\, ×\, R\, ×\, T}{100} \)
∴ 340 = \(\large \frac{1700 \, ×\, R\, ×\, 2}{100} \)
∴ 340 = \(\large \frac{3400 \, ×\, R}{100} \)
∴ 340 = 34 × R
∴ R = \( \frac{340}{34} \)
∴ R = 10 p.c.p.a
OPTION (iv)
2. If the interest on 3000 rupees is 600 rupees at a certain rate for a certain number of years, what would the interest be on 1500 rupees under the same conditions ?
(i) 300 rupees
(ii) 1000 rupees
(iii) 700 rupees
(iv) 500 rupees
Given:
\( P_1 \) = Rs 3000
\( I_1 \) = Rs 600
\( T_1 \) = \( T_2 \)
\( R_1 \) = \( R_2 \)
\( P_2 \) = Rs 1500
To find:
\( I_2 \)
Solution:
Total interest = \(\large \frac{P\, ×\, R\, ×\, T}{100} \)
∴ \( I_1 \) = \(\large \frac{P_1\, ×\, R_1\, ×\, T_1}{100} \)
∴ 600 = \(\large \frac{3000\, ×\, R_1\, ×\, T_1}{100} \)
∴ \(\large \frac{600\, ×\, 100}{3000} \) = \( R_1 \) × \( T_1 \)
∴ \( R_1 \) × \( T_1 \) = \(\large \frac{60000}{3000} \)
∴ \( R_1 \) × \( T_1 \) = 20 …(i)
And,
∴ \( I_2 \) = \(\large \frac{P_2\, ×\, R_2\, ×\, T_2}{100} \)
∴ \( I_2 \) = \(\large \frac{1500\, ×\, R_2\, ×\, T_2}{100} \)
∴ \( I_2 \) = \(\large \frac{1500\, ×\, R_1\, ×\, T_1}{100} \) [∵ \( T_1 \) = \( T_2 \), \( R_1 \) = \( R_2 \)]
∴ \( I_2 \) = \(\large \frac{1500\, ×\, 20}{100} \)
∴ \( I_2 \) = \(\large \frac{30000}{100} \)
∴ \( I_2 \) = Rs 300
OPTION (i)
3. Javed deposited 12000 rupees at 9 p.c.p.a. in a bank for some years, and withdrew his interest every year. At the end of the period, he had received altogether 17,400 rupees. For how many years had he deposited his money ?
Given:
P = Rs 12000
R = 9 p.c.p.a
Amount = Rs 17400
To find:
T
Solution:
Amount = Principal + Interest
∴ 17400 = 12000 + Interest
∴ Interest = 17400 – 12000
∴Interest = Rs 5400
∴ Total interest = \( \frac{P\, ×\, R\, ×\, T}{100} \)
5400 = \( \frac{12000\, ×\, 9\, ×\, T}{100} \)
∴ \( \frac{5400\, ×\, 100}{12000\, ×\, 9} \) = T
∴ T = 5 years
Ans: Javed had deposited the amount for 5 years.
4. Lataben borrowed some money from a bank at a rate of 10 p.c.p.a. interest for 2½ years to start a cottage industry. If she paid 10250 rupees as total interest, how much money had she borrowed ?
Given:
R = 10 p.c.p.a
T = 2.5 years
I = Rs 10250
To find:
P
Solution:
Total interest = \(\large \frac{P\, ×\, R\, ×\, T}{100} \)
10250 = \(\large \frac{P\, ×\, 10\, ×\, 2.5}{100} \)
10250 = \(\large \frac{P\, ×\, 25}{100} \)
\(\large \frac{10250\, ×\, 100}{25} \) = P
P = 10250 × 4
∴ P = Rs 41000
Ans: Lataben had borrowed an amount of Rs 41000 from the bank.
5. Fill in the blanks in the table.
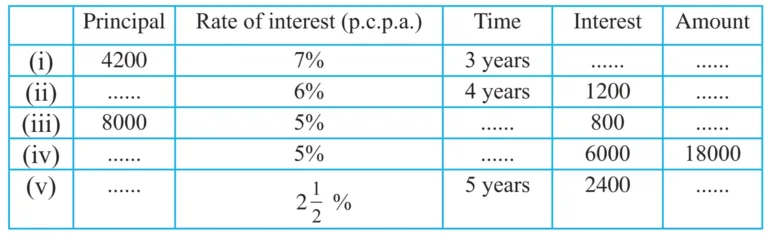
1.
Given:
P = Rs 4200
R = 7 p.c.p.a
T = 3 years
To find:
Total Interest and Amount
Solution:
Total interest = \(\large \frac{P\, ×\, R\, ×\, T}{100} \)
Total interest = \(\large \frac{4200\, ×\, 7\, ×\, 3}{100} \)
Total interest = Rs 882
Amount = Principal + Interest
Amount = 4200 + 882
Amount = Rs 5082
Ans: Total interest is Rs 882 and Amount is Rs 5082.
2.
Given:
I = Rs 1200
R = 6 p.c.p.a
T = 4 years
To find:
Principal and Amount
Solution:
Total interest = \(\large \frac{P\, ×\, R\, ×\, T}{100} \)
∴ 1200 = \(\large \frac{P\, ×\, 6\, ×\, 4}{100} \)
∴ \(\large \frac{1200\, ×\, 100}{6\, ×\, 4} \) = P
∴ Principal = Rs 5000
Amount = Principal + Interest
Amount = 5000 + 1200
Amount = Rs 6200
Ans: Principal is Rs 5000 and Amount is Rs 6200
3.
Given:
P = Rs 8000
R = 5 p.c.p.a
I = Rs 800
To find:
Time and Amount
Solution:
Total interest = \(\large \frac{P\, ×\, R\, ×\, T}{100} \)
∴ 800 = \(\large \frac{800\, ×\, 5\, ×\, T}{100} \)
∴ \(\large \frac{800\, ×\, 100}{8000\, ×\, 5} \) = T
∴ Time = 2 years
Amount = Principal + Interest
∴ Amount = 8000 + 800
∴ Amount = Rs 8800
Ans: Time is 2 years and Amount is Rs 8800.
4.
Given:
A = Rs 18000
R = 5 p.c.p.a
I = Rs 6000 years
To find:
Principal and Time
Solution:
Amount = Principal + Interest
∴ 18000 = Principal + 6000
∴ Principal = Rs 12000
Total interest = \(\large \frac{P\, ×\, R\, ×\, T}{100} \)
∴ 6000 = \(\large \frac{12000\, ×\, 5\, ×\, T}{100} \)
∴ \(\large \frac{6000\, ×\, 100}{12000\, ×\, 5} \) = T
∴ Time = 10 years
Ans: Principal is Rs 12000 and Time is 10 years.
5.
Given:
P = Rs 4200
R = 2½ p.c.p.a = 2.5 p.c.p.a
I = Rs 2400
To find:
Principal and Amount
Solution:
R = 2½ % = 2.5 %
∴ Total interest = \(\large \frac{P\, ×\, R\, ×\, T}{100} \)
∴ 2400 = \(\large \frac{P\, ×\, 25\, ×\, 5}{100} \)
∴ 2400 = \(\large \frac{P\, ×\, 25\, ×\, 5}{100\, ×\, 10} \)
∴ \(\large \frac{2400\, ×\, 10\, ×\, 100}{25\, ×\, 5} \) = P
∴ Principal = Rs 19200
Amount = Principal + Interest
∴ Amount = 19200 + 2400
∴ Amount = Rs 21600
Ans: Principal is Rs 19200 and Amount is Rs 21600.
