Chapter 1 – Geometrical Constructions
Practice Set 1
1. Draw line segments of the lengths given below and draw their perpendicular bisectors.
(1) 5.3 cm
Solution:
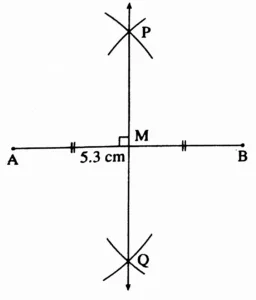
Line PQ is the perpendicular bisector of seg AB.
(2) 6.7 cm
Solution:
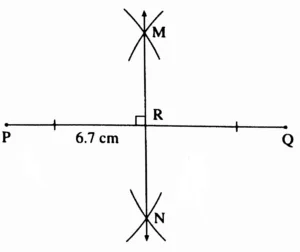
Line MN is the perpendicular bisector of seg PQ.
(3) 3.8 cm
Solution:
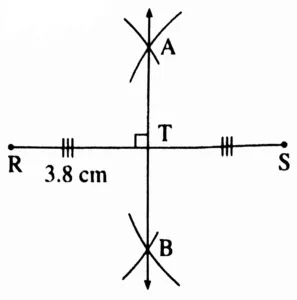
Line AB is the perpendicular bisector of seg RS.
2. Draw angles of the measures given
below and draw their bisectors.
(1) 105°
Solution:
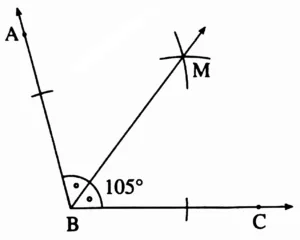
Ray BM is the bisector of ∠ABC.
(2) 55°
Solution:
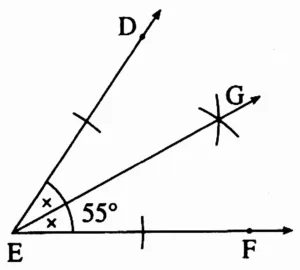
Ray EG is the bisector of ∠DEF.
(3) 90°
Solution:
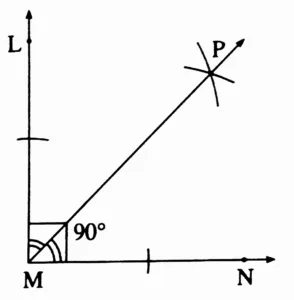
Ray MP is the bisector of ∠LMN.
3. Draw an obtuse-angled triangle and a right-angled triangle. Find the points of concurrence of the angle bisectors of each triangle. Where do the points of concurrence lie?
Solution:
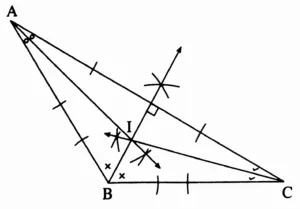
Obtuse angled triangle
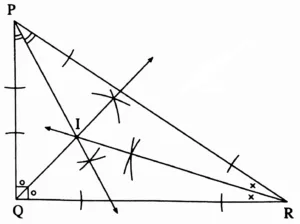
Right angled triangle
The point of concurrence of the angle bisectors in obtuse angled triangle and right angled triangle lie in their interior.
4. Draw a right-angled triangle. Draw the perpendicular bisectors of its sides. Where does the point of concurrence lie?
Solution:
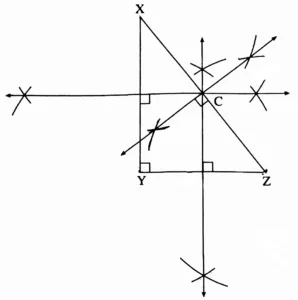
The perpendicular bisectors of the sides of a right angled triangle are concurrent. The point of concurrence C lies at the midpoint of the hypotenuse.
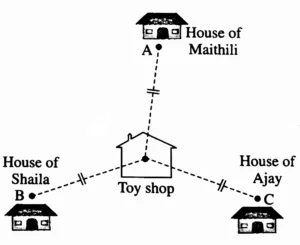
5 . Maithili, Shaila and Ajay live in three different places in the city. A toy shop is equidistant from the three houses. Which geometrical construction should be used to represent this? Explain your answer.
Solution:
Consider the position of three houses as three points. Assume that the houses are not in the same line.
We draw a rough figure showing the positions of the three houses.
A triangle is formed by joining the three points denoting the houses. To find the location of the toy shop which is equidistant from the houses, draw the perpendicular bisectors of the sides of the triangle so formed. The point of concurrence of the perpendicular bisectors of the sides of the triangle is the location of the toy shop.
Practice Set 2
1. Draw triangles with the measures given below.
(a) In ∆ABC, l(AB) = 5.5 cm, l(BC) = 4.2 cm, l(AC) = 3.5 cm
Ans:
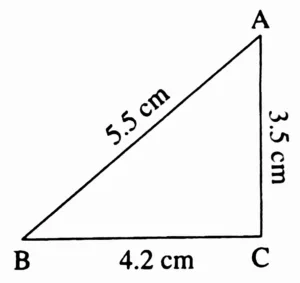
Rough Figure
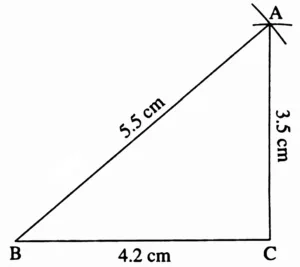
This is the required construction.
(b) In ∆STU, l(ST) = 7 cm, l(TU) = 4 cm, l(SU) = 5 cm
Ans:
Rough Figure
This is the required construction.
(c) In ∆PQR, l(PQ) = 6 cm, l(QR) = 3.8 cm, l(PR) = 4.5 cm
Ans:
Rough Figure
This is the required construction.
2. Draw an isosceles triangle with base 5 cm and the other sides 3.5 cm each.
Ans:
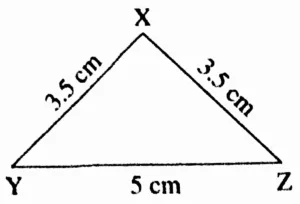
Rough Figure
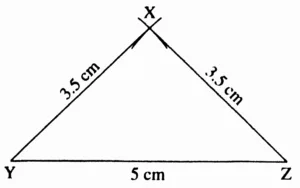
This is the required construction.
3. Draw an equilateral triangle with side 6.5 cm.
Ans:
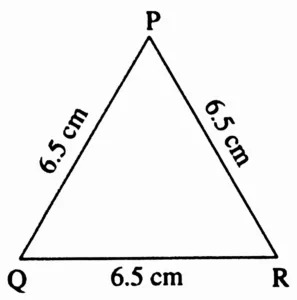
Rough Figure
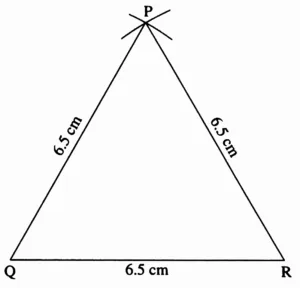
This is the required construction.
4. Choose the lengths of the sides yourself and draw one equilateral, one isosceles and one scalene triangle.
Ans:
Equilateral Triangle:
In ∆ABC l(AB) = l(BC) = l(AC) = 4.2 cm
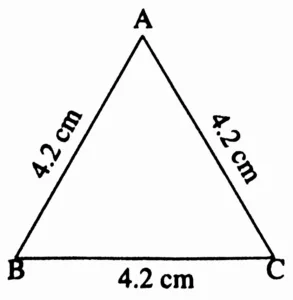
Rough Figure
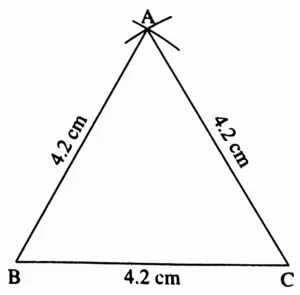
This is the required construction.
Isosceles Triangle:
In ∆PQR l(QR) = 5.8 cm l(PQ) = l(PR) = 4.7 cm
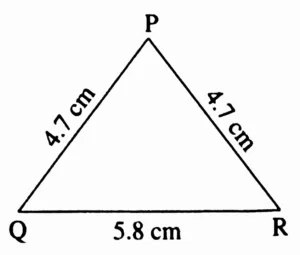
Rough Figure
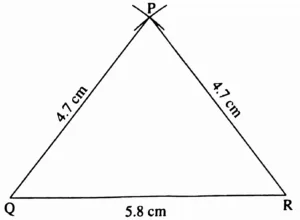
This is the required construction.
Scalene Triangle:
In ∆DEF l(DE) = 4 cm, l(EF) = 5 cm l(DF) = 6 cm
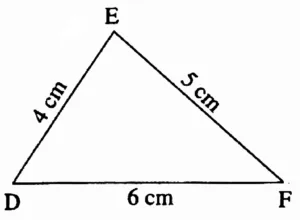
Rough Figure
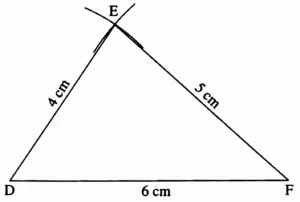
This is the required construction.
Practice Set 3
Draw triangles with the measures given below.
1. In ∆MAT, l(MA) = 5.2 cm, m∠A = 80°, l(AT) = 6 cm
Ans:
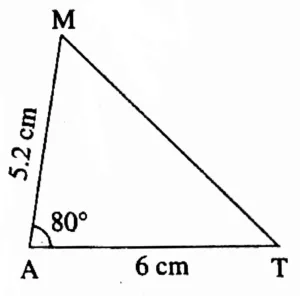
Rough Figure
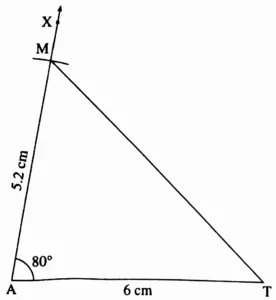
This is the required construction.
2. In ∆NTS, m∠T = 40°, l(NT) = l(TS) = 5 cm
Ans:
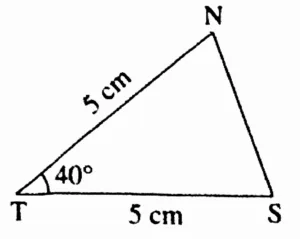
Rough Figure
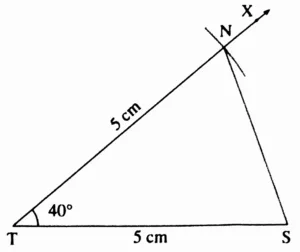
This is the required construction.
3. In ∆FUN, l(FU) = 5 cm, l(UN) = 4.6 cm, m∠U = 110°
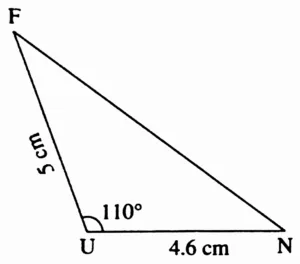
Rough Figure
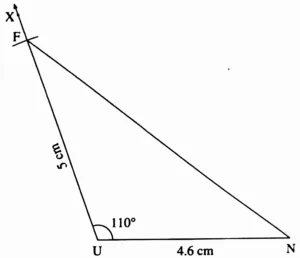
This is the required construction.
4. In ∆PRS, l(RS) = 5.5 cm, l(RP) = 4.2 cm, m∠R = 90°
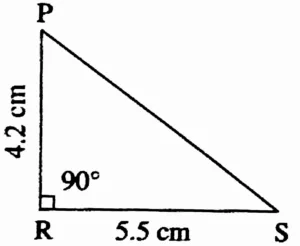
Rough Figure
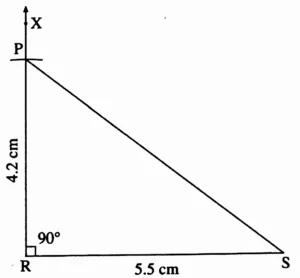
This is the required construction.
Practice Set 4
Construct triangles of the measures given below.
1. In ∆SAT, l(AT) = 6.4 cm, m∠A = 45°, m∠T = 105
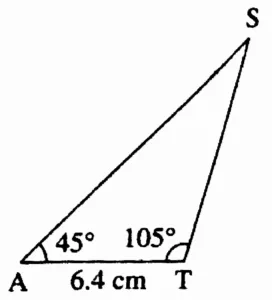
Rough Figure
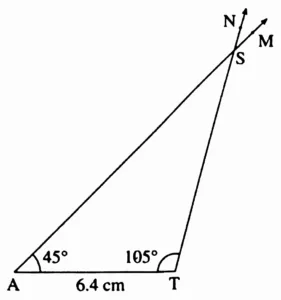
This is the required construction.
2. In ∆MNP, l(NP) = 5.2 cm, m∠N = 70°, m∠P = 40°
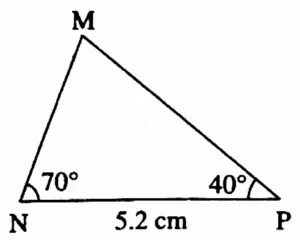
Rough Figure
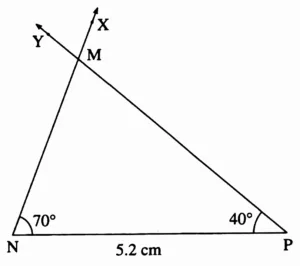
This is the required construction.
3. In ∆EFG, l(EG) = 6 cm, m∠F = 65°, m∠G = 45°
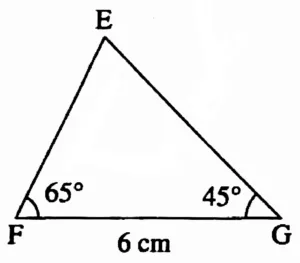
Rough Figure
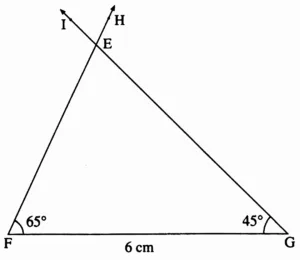
This is the required construction.
4. In ∆XYZ, l(XY) = 7.3 cm, m∠X = 34°, m∠Y = 95°
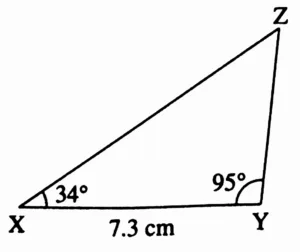
Rough Figure
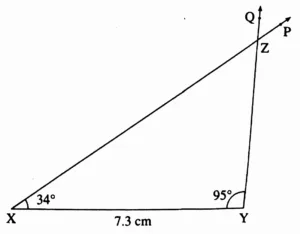
This is the required construction.
Practice Set 5
Construct triangles of the measures given below.
1. In ∆MAN, m∠MAN = 90°, l(AN) = 8 cm, l(MN) = 10 cm.
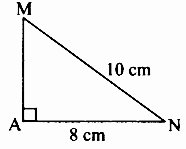
Rough Figure
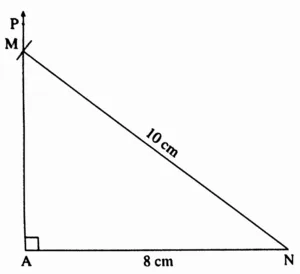
This is the required construction.
2. In the right-angled ∆STU, hypotenuse SU = 5 cm and l(ST) = 4 cm.
Ans:
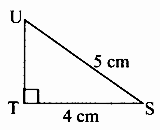
Rough Figure
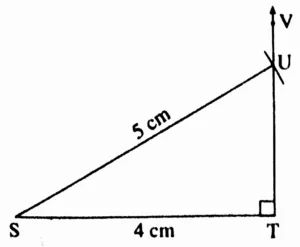
This is the required construction.
3. In ∆ABC, l(AC) = 7.5 cm, m∠ABC = 90°, l(BC) = 5.5 cm.
Ans:
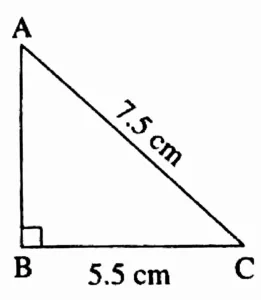
Rough Figure
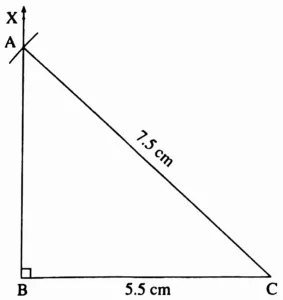
This is the required construction.
4. In ∆PQR, l(PQ) = 4.5 cm, l(PR) = 11.7 cm, m∠PQR = 90°.
Ans:
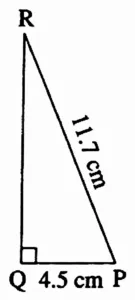
Rough Figure
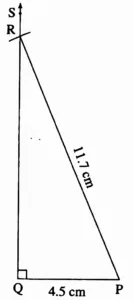
This is the required construction.
5. Students should take examples of their own and practise construction of triangles.
Practice Set 6
1. Write the names of pairs of congruent line segments. (Use a divider to find them.)
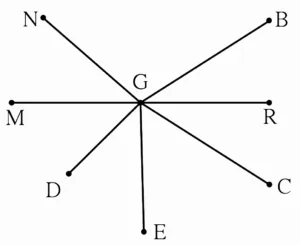
Ans:
seg GM ≅ seg GR
seg GN ≅ seg GE
seg GB ≅ seg GC
seg GM ≅ seg GN ≅ seg GR ≅ seg GE
2. On the line below, the distance between any two adjoining points shown on it is equal. Hence, fill in the blanks.

(i) seg AB ≅ seg _____
Ans: seg AB ≅ seg BC
(ii) seg AP ≅ seg _____
Ans: seg AP ≅ seg WQ
(iii) seg AC ≅ seg _____
Ans: seg AC ≅ seg WY
(iv) seg _____ ≅ seg BY
Ans: seg QX ≅ seg BY
(v) seg _____ ≅ seg YQ
Ans: seg XB ≅ seg YQ
(vi) seg BW ≅ seg _____
Ans: seg BW ≅ seg XZ
Practice Set 7
Some angles are given below. Using the symbol of congruence write the names of the pairs of congruent angles in these figures.
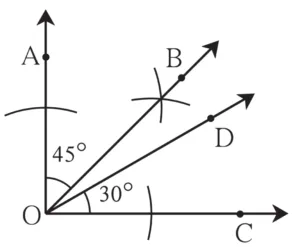
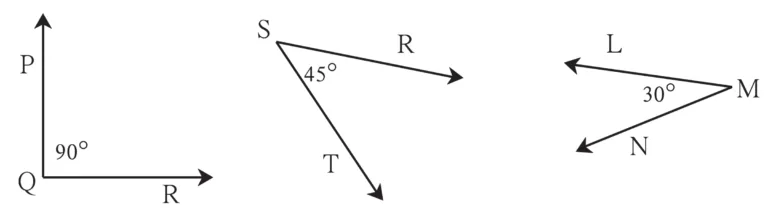
Some angles are given below. Using the symbol of congruence write the names of the pairs of congruent angles in these figures.
Ans:
∠AOB ≅ ∠BOC
∠AOB ≅ ∠BOC ≅ ∠RST
∠AOC ≅ ∠PQR
∠DOC ≅ ∠LMN
