Chapter 3 – Current Electricity
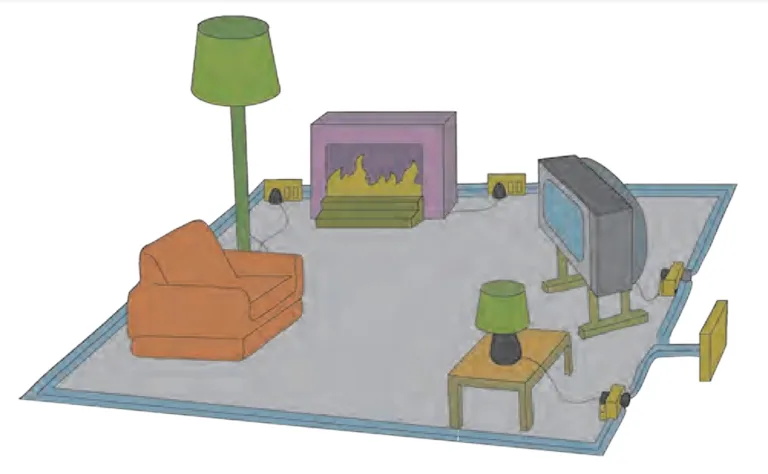
1. The accompanying figure shows some electrical appliances connected in a circuit in a house. Answer the following questions.
A. By which method are the appliances connected?
Ans: Appliances are connected in parallel.
B. What must be the potential difference across individual appliances?
Ans: The potential difference across all appliances is the same in parallel connection.
C. Will the current passing through each appliance be the same? Justify your answer.
Ans: No, as every appliance has a different load (resistance), current flowing through each appliance will be different.
D. Why are domestic appliances connected in this way?
Ans: The appliances are connected in parallel as the potential difference remains the same.
E. If the T.V. stops working, will the other appliances also stop working? Explain your answer.
Ans: No, the other devices will not stop working as the current flowing through them is along different paths.
2. The following figure shows the symbols for components used in the accompanying electrical circuit.
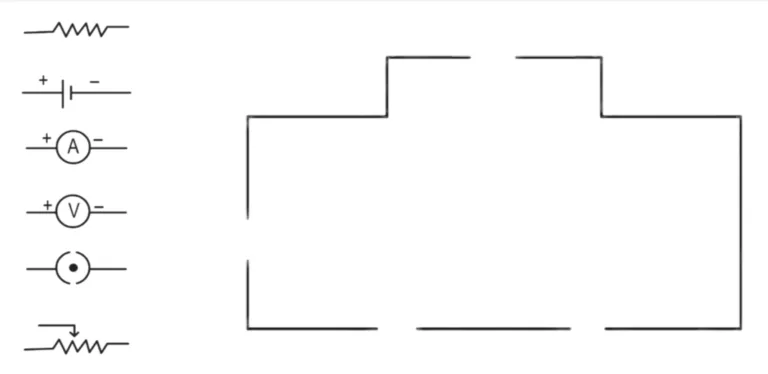
Place them at proper places and complete the circuit.
Ans:
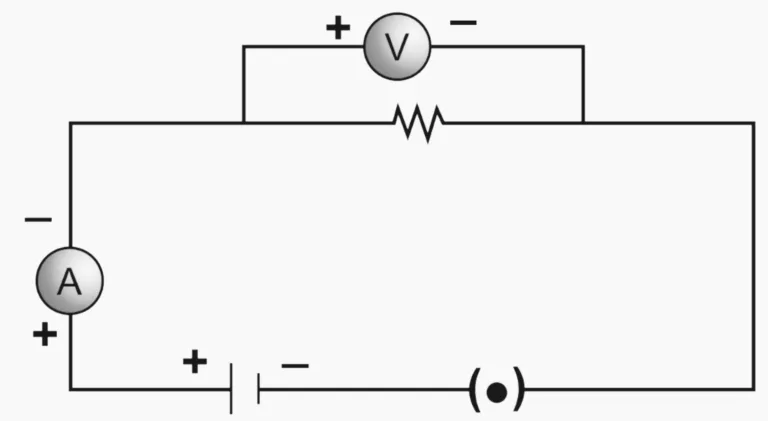
Which law can you prove with the help of the above circuit?
Ans: This circuit can be used to prove Ohm’s law.
3. Umesh has two bulbs having resistances of 15 W and 30 W. He wants to connect them in a circuit, but if he connects them one at a time the filament gets burnt. Answer the following.
A. Which method should he use to connect the bulbs?
Ans: Umesh should connect the bulbs in series combination.
B. What are the characteristics of this way of connecting the bulbs depending on the answer of question A above?
Ans:
(i) Bulbs are connected in series.
(ii) Overall resistance will increase and hence current will decrease.
(iii) So the filament of the bulb will not get burnt.
C. What will be the effective resistance in the above circuit?
Ans: The effective resistance in the circuit will be
Rₛ = R₁ + R₂
∴ Rₛ = 15 + 30
∴ Rₛ = 45 Ω
4. The following table shows current in Amperes and potential difference in Volts.
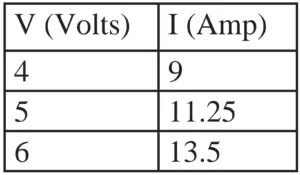
a. Find the average resistance.
Ans:
V₁ = 4V, V₂ = 5V, V₃ = 6V
I₁ = 9A, I₂ = 11.25A, I₃ = 13.5A
R₁ = \(\large \frac {V₁}{I₁}\)
∴ R₁ = \(\large \frac {4}{9}\)
∴ R₁ = 0.44 Ω
R₂ = \(\large \frac {V₂}{I₂}\)
∴ R₂ = \(\large \frac {5}{11.25}\)
∴ R₂ = 0.44 Ω
R₃ = \(\large \frac {V₃}{I₃}\)
∴ R₃ = \(\large \frac {6}{13.5}\)
∴ R₃ = 0.44 Ω
Average resistance = \(\large \frac {R₁ \,+\,R₂ \,+\, R₃}{13.5}\)
Average resistance = \(\large \frac {0.44 \,+\,0.44\,+\, 0.44}{3}\)
Average resistance = 0.44 Ω
b. What will be the nature of the graph between the current and potential difference? (Do not draw a graph.)
Ans: Graph will be linear as current and potential difference are directly proportional.
c. Which law will the graph prove? Explain the law.
Ans: The graph proves Ohm’s Law. It states that “If the physical state of a conductor remains constant, the current (I) flowing through it is directly proportional to the potential difference (V) between its two ends”.
5. Match the pairs

Ans: (1 – c), (2 – a), (3 – d), (4 – b)
6. The resistance of a conductor of length x is r. If its area of cross-section is a, what is its resistivity? What is its unit?
Ans:
Resistance (R) = r
Length (L) = x
Area of cross section (A) = a
Resistivity (ρ) = ?
We know that,
R = \(\large \frac {ρL}{A}\)
ρ = \(\large \frac {RA}{L}\)
ρ = \(\large \frac {ra}{x}\) Ωm
Its unit is ohm-metre (Ωm)
7. Resistances R₁, R2, R3 and R4 are connected as shown in the figure. S1 and S2 are two keys. Discuss the current flowing in the circuit in the following cases.
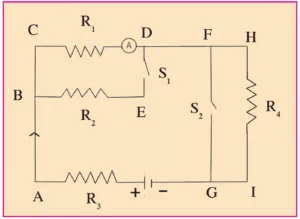
a. Both S₁ and S₂ are closed.
Ans: When both S₁ and S₂ are closed, the effective resistance of the circuit decreases and hence current will increase.
b. Both S₁ and S₂ are open.
Ans: When both S₁ and S₂ are open, the effective resistance of the circuit increases and hence current will decrease.
c. S₁ is closed but S₂ is open.
Ans: When S₁ is closed and S₂ is open, the effective resistance of the circuit decreases and hence current will l increase.
8. Three resistances x₁, x₂ and x₃ are connected in a circuit in different ways. x is the effective resistance. The properties observed for these different ways of connecting x₁, x₂ and x₃ are given below. Write the way in which they are connected in each case. (I-current, V-potential difference, x-effective resistance)
a. Current I flows through x₁, x₂ and x₃
Ans: If I is total current and same current I flows through x₁, x₂ and x₃, then the three resistors are connected in series combination.
b. x is larger than x₁, x₂ and x₃
Ans: As x is larger than x₁, x₂ and x₃, they are connected in series. As effective resistance in series is greater than individual resistance.
c. x is smaller than x₁, x₂ and x₃
Ans: As x is smaller than x₁, x₂ and x₃, they are connected in parallel. As effective resistance in parallel is smaller than individual resistance.
d. The potential difference across x₁, x₂ and x₃ is the same
Ans: As the potential difference across x₁, x₂ and x₃ is the same, they are connected in parallel.
e. x₁ + x₂ + x₃
Ans: x = x₁ + x₂ + x₃ is the formula for effective resistance in the circuit when resistances are connected in series.
f. x = \(\large \frac {1}{\large \frac {1}{x₁}\,+\,\large \frac {1}{x₂}\,+\,\large \frac {1}{x₃}}\)
Ans: This can also be expressed as;
\(\large \frac {1}{x}\) = \(\large \frac {1}{x₁}\) + \(\large \frac {1}{x₂}\) + \(\large \frac {1}{x₃}\)
This is the formula for the effective resistance of the circuit when resistors are connected in parallel.
9. Solve the following problems.
A. The resistance of a 1 m long nichrome wire is 6 Ω. If we reduce the length of the wire to 70 cm. What will its resistance be?
Given:
R₁ = 6 Ω
L₁ = 100 cm
L₂ = 70 cm
To find:
R₂
Solution:
ρ and A are the same in both cases So, resistance is directly proportional to the length of the wire.
∴ \(\large \frac {R₁}{R₂}\) = \(\large \frac {L₁}{L₂}\)
∴ \(\large \frac {6}{R₂}\) = \(\large \frac {100}{70}\)
∴ R₂ = \(\large \frac {6\,×\,70}{100}\)
∴ R₂ = 6 × 0.7
∴ R₂ = 4.2 Ω
Ans: The value of the resistance will change to 4.2 Ω
B. When two resistors are connected in series, their effective resistance is 80 Ω. When they are connected in parallel, their effective resistance is 20 Ω. What are the values of the two resistances?
Given:
Rs = 80 Ω
Rp = 20 Ω
To find:
R₁ and R₂
Solution:
Let R₁ and R₂ be the two resistances.
∴ R₁ + R₂ = 80
∴ R₂ = (80 – R₁) …(i)
Also,
\(\large \frac {1}{Rp}\) = \(\large \frac {1}{R₁}\) + \(\large \frac {1}{R₂}\) + \(\large \frac {1}{R₃}\)
\(\large \frac {1}{Rp}\) = \(\large \frac {R₁\,+\,R₂}{R₁\,×\,R₂}\)
Rp = \(\large \frac {R₁\,×\,R₂}{R₁\,+\,R₂}\)
20 = \(\large \frac {R₁(80\,–\,R₂)}{80}\)
1600 = 80 R₁ – R₁²
R₁² – 80 R₁ + 1600 = 0
R₁² – 40 R₁ – 40 R₁ + 1600 = 0
R₁(R₁ – 40) – 40(R₁ – 40) = 0
(R₁ – 40)(R₁ – 40) = 0
R₁ = 40 Ω
Now,
R₂ = (80 – R₁) …[From (i)]
R₂ = (40 – R₁)
R₂ = 40 Ω
Ans: The values of the two resistances R₁ and R₂ are 40 Ω and 40 Ω.
C. If a charge of 420 C flows through a conducting wire in 5 minutes what is the value of the current?
Given:
Electric charge (Q) = 420 ⁰C
Time (t) = 5 min = 5 × 60 = 300 sec
To find:
Electric current (I)
Solution:
We know that,
I = \(\large \frac {Q}{t}\)
I = \(\large \frac {420}{300}\)
I = 1.4 A
Ans: The current in the circuit is 1.4 A.
