Chapter 1 – Basic Concepts in Geometry
Practice set 1.1
1. Find the distances with the help of the number line given below.

(i) d(B,E)
Solution:
The coordinate of point B is 2.
The coordinate of point E is 5.
5 > 2
d(B, E) = Greater co–ordinate – smaller coordinate
d(B, E) = 5 – 2
d(B, E) = 3
Ans: d(B, E) = 3 units
(ii) d(J, A)
Solution:
The coordinate of point J is –2.
The coordinate of point A is 1.
1 > – 2
d(J, A) = Greater co–ordinate – smaller co–ordinate
d(J, A) = 1 – (–2)
d(J, A) = 1 + 2
d(J, A) = 3
Ans: d(J, A) = 3 units
(iii) d(P, C)
Solution:
The co–ordinate of point P is – 4.
The co–ordinate of point C is 3.
3 > – 4
d(P, C) = Greater co–ordinate – smaller co–ordinate
d(P, C) = 3 – (– 4)
d(P, C) = 3 + 4
d(P, C) = 7
Ans: d(P, C) = 7 units
(iv) d(J, H)
Solution:
The coordinate of point J is –2.
The coordinate of point H is –1.
– 1 > – 2
d(J, H) = Greater coordinate – smaller coordinate
d(J, H) = – 1 – (– 2)
d(J, H) = – 1 + 2
d(J, H) = 1
Ans: d(J, H) = 1 unit
(v) d(K, O)
Solution:
The coordinate of point K is –3.
The coordinate of point O is 0.
0 > –3
d(K, O) = Greater coordinate – smaller coordinate
d(K, O) = 0 – (–3)
d(K, O) = 0 + 3
d(K, O) = 3
Ans: d(K, O) = 3 units
(vi) d(O, E)
Solution:
The coordinate of point O is 0.
The coordinate of point E is 5.
5 > 0
d(O, E) = Greater coordinate – smaller coordinate
d(O, E) = 5 – 0
d(O, E) = 5
Ans: d(O, E) = 5 units
(vii) d(P, J)
Solution:
The coordinate of point P is – 4.
The coordinate of point J is – 2.
– 2 > – 4
d(P, J) = Greater coordinate – smaller coordinate
d(P, J) = – 2 – (– 4)
d(P, J) = – 2 + 4
d(P, J) = 2
Ans: d(P, J) = 2 units
(viii) d(Q, B)
Solution:
The coordinate of point Q is – 5.
The coordinate of point B is 2.
2 > – 5
d(Q, B) = Greater coordinate – smaller coordinate
d(Q, B) = 2 – (– 5)
d(Q, B) = 2 + 5
d(Q, B) = 7
Ans: d(Q, B) = 7 units
2. If the coordinate of A is x and that of B is y, find d(A, B).
(i) x = 1, y = 7
Solution:
The coordinate of point A is 1.
The coordinate of point B is 7.
7 > 1
d(A, B) = Greater coordinate – smaller coordinate
d(A, B) = 7 – 1
d(A, B) = 6
Ans: d(A, B) = 6 units
(ii) x = 6, y = – 2
Solution:
The coordinate of point A is 6.
The coordinate of point B is – 2.
6 > – 2
d(A, B) = Greater coordinate – smaller coordinate
d(A, B) = 6 – (– 2)
d(A, B) = 6 + 2
d(A, B) = 8
Ans: d(A, B) = 8 units
(iii) x = – 3, y = 7
Solution:
The coordinate of point A is – 3.
The coordinate of point B is 7.
7 > – 3
d(A, B) = Greater coordinate – smaller coordinate
d(A, B) = 7 – (– 3)
d(A, B) = 7 + 3
d(A, B) = 10
Ans: d(A, B) = 10 units
(iv) x = – 4, y = – 5
Solution:
The coordinate of point A is –4.
The coordinate of point B is –5.
– 4 > – 5
d(A, B) = Greater coordinate – smaller coordinate
d(A, B) = – 4 – (– 5)
d(A, B) = – 4 + 5
d(A, B) = 1
Ans: d(A, B) = 1 unit
(v) x = – 3, y = – 6
Solution:
The coordinate of point A is –3.
The coordinate of point B is – 6.
– 3 > – 6
d(A, B) = Greater coordinate – smaller coordinate
d(A, B) = – 3 – (– 6)
d(A, B) = – 3 + 6
d(A, B) = 3
Ans: d(A, B) = 3 units
(vi) x = 4, y = – 8
Solution:
The coordinate of point A is 4.
The coordinate of point B is – 8.
4 > – 8
d(A, B) = Greater coordinate – smaller coordinate
d(A, B) = 4 – (– 8)
d(A, B) = 4 + 8
d(A, B) = 12
Ans: d(A, B) = 12 units
3. From the information given below, find which of the points is between the other two. If the points are not collinear, state so.
(i) d(P, R) = 7, d(P, Q) = 10, d(Q, R) = 3
Solution:
d(P, Q) = 10 …(i)
d(P, R) + d(Q, R) = 7 + 3
∴ d(P, R) + d(Q, R) = 10 …(ii)
∴ d(P, Q) = d(P, R) + d(Q, R) …[From (i) and (ii)]
∴ Points P, Q and R are collinear points.
∴ Relation of betweenness exists, P – R – Q.
(ii) d(R, S) = 8, d(S, T) = 6, d(R, T) = 4
Solution:
d(R, S) = 8 …(i)
d(S, T) + d(R, T) = 6 + 4
∴ d(S, T) + d(R, T) = 10 …(ii)
∴ d(R, S) ≠ d(S, T) + d(R, T) …[From (i) and (ii)]
∴ Points R, S and T are non-collinear points.
∴ Relation of betweenness does not exist.
(iii) d(A, B) = 16, d(C, A) = 9, d(B, C) = 7
Solution:
d(A, B) = 16 ….. (i)
d(C, A) + d(B, C) = 9 + 7
∴ d(C, A) + d(B, C) = 16 ….. (ii)
∴ d(A, B) = d(C, A) + d(B, C) …[From (i) and (ii)]
∴ Points A, B and C are collinear points.
∴ Relation of betweenness exists, A – C – B.
(iv) d(L, M) = 11, d(M, N) = 12, d(N, L) = 8
Solution:
d(M, N) = 12 …(i)
d(L, M) + d(N, L) = 11 + 8
∴ d(L, M) + d(N, L) = 19 …(ii)
∴ d(M, N) ≠ d(L, M) + d(N, L) …[From (i) and (ii)]
∴ Points L, M and N are non-collinear points.
∴ Relation of betweenness does not exist.
(v) d(X, Y) = 15, d(Y, Z) = 7, d(X, Z) = 8
Solution:
d(X, Y) = 15 …(i)
d(Y, Z) + d(X, Z) = 7 + 8
∴ d(Y, Z) + d(X, Z) = 15 ….. (ii)
∴ d(X, Y) = d(Y, Z) + d(X, Z) …[From (i) and (ii)]
∴ Points X, Y and Z are collinear points.
∴ Relation of betweenness exists, X – Z – Y.
(vi) d(D, E) = 5, d(E, F) = 8, d(D, F) = 6
Solution:
d(E, F) = 8 …(i)
d(D, E) + d(D, F) = 5 + 6
∴ d(D, E) + d(D, F) = 11 …(ii)
∴ d(E, F) ≠ d(D, E) + d(D, F) …[From (i) and (ii)]
∴ Points D, E and F are non-collinear points.
∴ Relation of betweenness does not exist.
4. On a number line, points A, B and C are such that d(A, C) = 10, d(C, B) = 8. Find d(A, B) considering all possibilities.
Solution:
Case (i):
Consider A – B – C
∴ d(A, C) = d(A, B) + d(B, C)
∴ 10 = d(A, B) + 8
∴ 10 – 8 = d(A, B)
∴ d(A, B) = 2 units
Case (ii):
Consider A – C – B
∴ d(A, B) = d(A, C) + d(C, B)
∴ d(A, B) = 10 + 8
∴ d(A, B) = 18 units
Case (iii):
Consider B – A – C
∴ d(A, B) + d(A, C) = d(C, B)
∴ d(A, B) + 10 = 8
∴ d(A, B) = 8 – 10
∴ d(A, B) = – 2
But the distance between two points cannot be negative.
∴ B – A – C is not possible.
∴ d(A, B) = 2 units or d(A, B) = 18 units
Ans: d(A, B) can be 2 units or 18 units.
5. Points X, Y, Z are collinear such that d(X, Y) = 17, d(Y, Z) = 8, find d(X, Z).
Solution:
Case (i):
Consider X – Y – Z
∴ d(X, Z) = d(X, Y) + d(Y, Z)
∴ d(X, Z) = 17 + 8
∴ d(X, Z) = 25 units
Case (ii):
Consider X – Z – Y
∴ d(X, Y) = d(X, Z) + d(Z, Y)
∴ 17 = d(X, Z) + 8
∴ 17 – 8 = d(X, Z)
∴ d(X, Z) = 9 units
Case (iii):
Consider Y – X – Z
∴ d(X, Y) + d(X, Z) = d(Y, Z)
∴ 17 + d(X, Z) = 8
∴ d(X, Z) = – 17 + 8
∴ d(X, Z) = – 9 units
But, distance between two points cannot be negative.
Y – X – Z is not possible.
∴ d(X, Z) = 25 units or d(X, Z) = 9 units
Ans: d(X, Z) can be 9 units or 25 units.
6. Sketch a proper figure and write the answers of the following questions.
(i) If A – B – C and l(AC) = 11, l(BC) = 6.5, then l(AB) = ?
Solution:
A – B – C …[Given]
l(AC) = l(AB) + l(BC)
11 = l(AB) + 6.5
11 – 6.5 = l(AB)
l(AB) = 4.5 units
Ans: l(AB) = 4.5 units
Figure:
(ii) If R – S – T and l(ST) = 3.7, l(RS) = 2.5, then l(RT) = ?
Solution:
R – S – T …[Given]
l(RT) = l(RS) + l(ST)
l(RT) = 2.5 + 3.7
l(RT) = 6.2 units
Ans: l(RT) = 6.2 units
Figure:

(iii) If X – Y – Z and l(XZ) = 3 \(\sqrt {7}\), l(XY) = \(\sqrt {7}\), then l(YZ) = ?
Solution:
X – Y – Z …[Given]
l(XZ) = l(XY) + l(YZ)
3 \(\sqrt {7}\) = \(\sqrt {7}\) + l(YZ)
3 \(\sqrt {7}\) – \(\sqrt {7}\) = l(YZ)
l(YZ) = 2 \(\sqrt {7}\) units
Ans: l(YZ) = 2 \(\sqrt {7}\) units
Figure:

7. Which figure is formed by three non-collinear points ?
Ans: Three non-collinear points join to form a triangle.
Figure:
Practice set 1.2
1. The following table shows points on a number line and their coordinates. Decide whether the pair of segments given below the table are congruent or not.

(i) seg DE and seg AB
Solution:
The coordinate of point D is – 7.
The coordinate of point E is 9.
9 > – 7
d(D, E) = Greater coordinate – Smaller co-ordinate
d(D, E) = 9 – (– 7)
d(D, E) = 9 + 7
d(D, E) = 16
∴ l(DE) = 16 units ….(i)
The coordinate of point A is – 3.
The coordinate of point B is 5.
5 > – 3
d(A, B) = Greater coordinate – Smaller coordinate
d(A, B) = 5 – (– 3)
d(A, B) = 5 + 3
d(A, B) = 8
l(AB) = 8 units …(ii)
∴ l(DE) ≠ l(AB) …[From (i) and (ii)]
Ans: Seg DE is not congruent to seg AB.
(ii) seg BC and seg AD
Solution:
The coordinate of point B is 5.
The coordinate of point C is 2.
5 > 2
d(B, C) = Greater coordinate – Smaller coordinate
d(B, C) = 5 – 2
d(B, C) = 3
l(BC) = 3 units …(i)
The coordinate of point A is – 3.
The coordinate of point D is – 7.
– 3 > – 7
d(A, D) = Greater coordinate – Smaller coordinate
d(A, D) = – 3 – (– 7)
d(A, D) = – 3 + 7
d(A, D) = 4
l(AD) = 4 units …(ii)
∴ l(BC) ≠ l(AD) …[From (i) and (ii)]
Ans: Seg BC is not congruent to seg AD.
(iii) seg BE and seg AD
Solution:
The coordinate of point B is 5.
The coordinate of point E is 9.
9 > 5
d(B, E) = Greater coordinate – Smaller coordinate
d(B, E) = 9 – 5
d(B, E) = 4
l(BE) = 4 units …(i)
The coordinate of point A is – 3.
The coordinate of point D is – 7.
– 3 > – 7
d(A, D) = Greater coordinate – Smaller coordinate
d(A, D) = – 3 – (– 7)
d(A, D) = – 3 + 7
d(A, D) = 4
l(AD) = 4 units …(ii)
∴ l(BE) = l(AD) …[From (i) and (ii)]
Ans: seg BE ≅ seg AD
2. Point M is the midpoint of seg AB. If AB = 8 then find the length of AM.
Solution:
M is the midpoint of seg AB …[Given]
l(AM) = \(\large \frac {1}{2}\) l(AB)
l(AM) = \(\large \frac {1}{2}\) × 8
l(AM) = 4 units
Ans: l(AM) = 4 units
3. Point P is the midpoint of seg CD. If CP = 2.5, find l(CD).
Solution:
Point P is the midpoint of seg CD …[Given]
l(CP) = \(\large \frac {1}{2}\) l(CD)
2.5 = \(\large \frac {1}{2}\) l(CD)
l(CD) = 2.5 × 2
l(CD) = 5 units
Ans: l(CD) = 5 units
4. If AB = 5 cm, BP = 2 cm and AP = 3.4 cm, compare the segments.
Solution:
AB = 5 cm, BP = 2 cm, AP = 3.4 cm
5 > 3.4 > 2
∴ l(AB) > l(AP) > l(BP)
5. Write the answers to the following questions with reference to figure 1.13.

(i) Write the name of the opposite ray of ray RP.
Ans: Ray RS is opposite of ray RP.
(ii) Write the intersection set of ray PQ and ray RP.
Ans: Intersection set of ray PQ and ray RP is ray PQ.
(iii) Write the union set of seg PQ and seg QR.
Ans: The union of ray PQ and ray QR is line QR.
(iv) State the rays of which seg QR is a subset.
Ans: Seg QR is a subset of ray QR, ray RQ, ray QS and ray QT.
(v) Write the pair of opposite rays with common end point R.
Ans: Ray RP and ray RS.
(vi) Write any two rays with common endpoint S.
Ans: Ray ST and ray SR.
(vii) Write the intersection set of ray SP and ray ST.
Ans: The intersection of ray SP and ray ST is point S.
6. Answer the questions with the help of figure 1.14.

(i) State the points which are equidistant from point B.
Ans:
(a) Point A and Point C.
(b) Point P and Point D.
(ii) Write a pair of points equidistant from point Q.
Ans: Point R and point P.
(iii) Find d(U, V), d(P, C), d(V, B), d(U, L).
Solution:
d(U, V)
The coordinate of point U is – 5.
The coordinate of point V is 5.
5 > – 5
d(U, V) = Greater coordinate – Smaller coordinate
d(U, V) = 5 – (– 5)
d(U, V) = 5 + 5
∴ d(U, V) = 10 Units
d(P, C)
The coordinate of point P is – 2.
The coordinate of point C is 4.
4 > – 2
d(P, C) = Greater coordinate – Smaller coordinate
d(P, C) = 4 – (– 2)
d(P, C) = 4 + 2
∴ d(P, C) = 6 Units
d(V, B)
The coordinate of point V is 5.
The coordinate of point B is 2.
5 > 2
d(V, B) = Greater coordinate – Smaller coordinate
∴ d(V, B) = 5 – 2
∴ d(V, B) = 3 Units
d(U, L)
The coordinate of point U is – 5.
The coordinate of point L is – 3.
– 3 > – 5
d(U, L) = Greater coordinate – Smaller coordinate
d(U, L) = – 3 – (– 5)
d(U, L) = – 3 + 5
∴ d(U, L) = 2 Units
Ans:
d(U, V) = 10 Units
d(P, C) = 6 Units
d(V, B) = 3 Units
d(U, L) = 2 Units
Practice set 1.3
1. Write the following statements in ‘if–then’ form.
(i) The opposite angles of a parallelogram are congruent.
Ans: If a quadrilateral is a parallelogram then its opposite angles are congruent.
(ii) The diagonals of a rectangle are congruent.
Ans: If a quadrilateral is a rectangle then its diagonals are congruent.
(iii) In an isosceles triangle, the segment joining the vertex and the midpoint of the base is perpendicular to the base.
Ans: If a triangle is an isosceles triangle, then the segment joining the vertex and midpoint of the base is perpendicular to the base.
2. Write converses of the following statements.
(i) The alternate angles formed by two parallel lines and their transversal are congruent.
Ans: Converse statement:
If alternate angles formed by two lines and its transversal are congruent then the lines are parallel.
(ii) If a pair of the interior angles made by a transversal of two lines are supplementary then the lines are parallel.
Ans: Converse statement:
If two parallel lines are intersected by a transversal then interior angles so formed are supplementary.
(iii) The diagonals of a rectangle are congruent.
Ans: Converse statement:
If the diagonals of a quadrilateral are congruent then that quadrilateral is rectangle.
Problem Set 1
1. Select the correct alternative from the answers of the questions given below.
(i) How many midpoints does a segment have?
(A) only one
(B) two
(C) three
(D) many
Ans: Option (A) : only one
(ii) How many points are there in the intersection of two distinct lines ?
(A) infinite
(B) two
(C) one
(D) not a single
Ans: Option (C) : one
(iii) How many lines are determined by three distinct points?
(A) two
(B) three
(C) one or three
(D) six
Ans: Option (C) : one or three
(iv) Find d(A, B), if co-ordinates of A and B are – 2 and 5 respectively.
(A) – 2
(B) 5
(C) 7
(D) 3
Ans: Option (C) : 7
Solution:
– 2 < 5
∴ d(A, B) = Greater co-ordinate – Smaller co-ordinate
∴ d(A, B) = 5 – (– 2)
∴ d(A, B) = 5 + 2
∴ d(A, B) = 7 units
(v) If P – Q – R and d(P, Q) = 2, d(P, R) = 10, then find d(Q, R).
(A) 12
(B) 8
(C) 96
(D) 20
Ans: Option (B) : 8
Solution:
d(P, R) = d(P, Q) + d(Q, R) [∵ P – Q – R]
∴ 10 = 2 + d(Q, R)
∴ d(Q, R) = 10 – 2
∴ d(Q, R) = 8 units
2. On a number line, co-ordinates of P, Q, R are 3, – 5 and 6 respectively. State with reason whether the following statements are true or false.
Solution:
The co-ordinate of P is 3.
The co-ordinate of Q is – 5.
The co-ordinate of R is 6.
3 > – 5
∴ d(P, Q) = Greater co-ordinate – Smaller co-ordinate
∴ d(P, Q) = 3 – (– 5)
∴ d(P, Q) = 3 + 5
∴ d(P, Q) = 8 units
– 5 < 6
∴ d(Q, R) = Greater co-ordinate – Smaller co-ordinate
∴ d(Q, R) = 6 – (– 5)
∴ d(Q, R) = 6 + 5
∴ d(Q, R) = 11 units
6 > 3
∴ d(P, R) = Greater co-ordinate – Smaller co-ordinate
∴ d(P, R) = 6 – 3
∴ d(P, R) = 3 units
(i) d(P, Q) + d(Q, R) = d(P, R)
Solution:
d(P, Q) + d(Q, R) = 8 + 11
d(P, Q) + d(Q, R) = 19 units …(i)
d(P, R) = 3 units ….(ii)
∴ d(P, Q) + d(Q, R) ≠ d(P, R) …[From (i) and (ii)]
∴ d(P, Q) + d(Q, R) = d(P, R) is a false statement.
(ii) d(P, R) + d(R, Q) = d(P, Q)
Solution:
d(P, R) + d(Q, R) = 3 + 11
d(P, R) + d(Q, R) = 14 units …(i)
d(P, Q) = 8 units ….(ii)
∴ d(P, R) + d(R, Q) ≠ d(P, Q) …[From (i) and (ii)]
∴ d(P, R) + d(R, Q) = d(P, Q) is a false statement.
(iii) d(R, P) + d(P, Q) = d(R, Q)
Solution:
d(P, R) + d(P, Q) = 3 + 8
d(P, R) + d(P, Q) = 11 units …(i)
d(R, Q) = 11 units ….(ii)
∴ d(P, R) + d(P, Q) = d(R, Q) …[From (i) and (ii)]
∴ d(P, R) + d(R, Q) = d(P, Q) is a true statement.
(iv) d(P, Q) – d(P, R) = d(Q, R)
Solution:
d(P, Q) – d(P, R) = 8 – 3
d(P, Q) – d(P, R) = 5 units …(i)
d(R, Q) = 11 units ….(ii)
∴ d(P, R) + d(P, Q) ≠ d(R, Q) …[From (i) and (ii)]
∴ d(P, R) + d(R, Q) = d(P, Q) is a true statement.
3. Co-ordinates of some pairs of points are given below. Hence find the distance between each pair.
(i) 3, 6
Solution:
Let,
The co-ordinate of point A be 3
The co-ordinate of point B be 6
6 > 3
d(A, B) = Greater co-ordinate – Smaller co-ordinate
∴ d(A, B) = 6 – 3
∴ d(A, B) = 3
∴ d(A, B) = 3
Ans: The distance between the given pair of points is 3 units.
(ii) – 9, – 1
Solution:
Let,
The co-ordinate of point A be – 9
The co-ordinate of point B be – 1
– 1 > – 9
d(A, B) = Greater co-ordinate – Smaller co-ordinate
∴ d(A, B) = – 1 – (– 9)
∴ d(A, B) = – 1 + 9
∴ d(A, B) = 8
∴ d(A, B) = 8 units
Ans: The distance between the given pair of points is 8 units.
(iii) – 4, 5
Solution:
Let,
The co-ordinate of point A be – 4
The co-ordinate of point B be 5
5 > – 4
d(A, B) = Greater co-ordinate – Smaller co-ordinate
∴ d(A, B) = 5 – (– 4)
∴ d(A, B) = 5 + 4
∴ d(A, B) = 9
∴ d(A, B) = 9 units
Ans: The distance between the given pair of points is 9 units.
(iv) 0, – 2
Solution:
Let,
The co-ordinate of point A be 0
The co-ordinate of point B be – 2
0 > – 2
d(A, B) = Greater co-ordinate – Smaller co-ordinate
∴ d(A, B) = 0 – (– 2)
∴ d(A, B) = 0 + 2
∴ d(A, B) = 2
Ans: The distance between the given pair of points is 2 units.
(v) x + 3, x – 3
Solution:
Let,
The co-ordinate of point A be x + 3
The co-ordinate of point B be x – 3
(x + 3) > (x – 3)
d(A, B) = Greater co-ordinate – Smaller co-ordinate
∴ d(A, B) = (x + 3) – (x – 3)
∴ d(A, B) = x + 3 – x + 3
∴ d(A, B) = 6
∴ d(A, B) = 6 units
Ans: The distance between the given pair of points is 6 units.
(vi) – 25, – 47
Solution:
Let,
The co-ordinate of A point be – 25
The co-ordinate of B point be – 47
– 25 > – 47
d(A, B) = Greater co-ordinate – Smaller co-ordinate
∴ d(A, B) = – 25 – (– 47)
∴ d(A, B) = – 25 + 47
∴ d(A, B) = 22 units
Ans: The distance between the given pair of points is 22 units.
(vii) 80, – 85
Solution:
Let,
The co-ordinate of point A be 80
The co-ordinate of point B be – 85
80 > – 85
d(A, B) = Greater co-ordinate – Smaller co-ordinate
∴ d(A, B) = 80 – (– 85)
∴ d(A, B) = 80 + 85
∴ d(A, B) = 165 units
Ans: The distance between the given pair of points is 165 units.
4. Co-ordinate of point P on a number line is – 7. Find the co-ordinates of points on the number line which are at a distance of 8 units from point P.
Solution:
Let Q = x be a point on the positive side of point P.
Co-ordinate of P is – 7
x > – 7
d(P, Q) = x – (– 7)
∴ 8 = x + 7
∴ x = 8 – 7
∴ x = 1
∴ Co-ordinate of point Q is 1.
Let R = y be a point on the negative side of point P.
Co-ordinate of point P is – 7
– 7 > y
∴ d(P, R) = – 7 – y
∴ 8 = – 7 – y
∴ 8 + 7 = – y
∴ – y = 15
∴ y = – 15
∴ Co-ordinate of point R is – 15
Ans: Co-ordinates of points at a distance of 8 units from point P is Q = 1 and R = – 15
5. Answer the following questions.
(i) If A – B – C and d(A, C) = 17, d(B, C) = 6.5 then d (A, B) = ?
Solution:
d(A, C) = d(A, B) + d(B, C) [∵ A – B – C]
17 = d(A, B) + 6.5
d(A, B) = 17 – 6.5
d(A, B) = 10.5 units
Ans: d(A, B) is 10.5 units.
(ii) If P – Q – R and d(P, Q) = 3.4, d(Q, R)= 5.7 then d(P, R) = ?
Solution:
d(P, R) = d(P, Q) + d(Q, R) [∵ P – Q – R]
d(P, R) = 3.4 + 5.7
d(P, R) = 9.1 units
Ans: d(P, R) is 9.1 units
6. Co-ordinate of point A on a number line is 1. What are the co-ordinates of points on the number line which are at a distance of 7 units from A?
7. Write the following statements in conditional form.
(i) Every rhombus is a square.
Ans: If a quadrilateral is a square then it is a rhombus.
(ii) Angles in a linear pair are supplementary.
Ans: If adjacent angles are supplementary, then they form a linear pair.
(iii) A triangle is a figure formed by three segments.
Ans: If a polygon is three-sided closed figure, then it is a triangle.
(iv) A number having only two divisors is called a prime number.
Ans: If a number is a prime number then it has only two divisors.
8. Write the converse of each of the following statements.
(i) If the sum of measures of angles in a figure is 180⁰, then the figure is a triangle.
Ans: If a figure is a triangle the sum of all angles of this figure is 180º.
(ii) If the sum of measures of two angles is 90⁰ then they are complement of each other.
Ans: If two angles are complementary then their sum is 90º.
(iii) If the corresponding angles formed by a transversal of two lines are congruent then the two lines are parallel.
Ans: If two parallel lines are intersected by a transversal then the pair of corresponding angles is congruent.
(iv) If the sum of the digits of a number is divisible by 3 then the number is divisible by 3.
Ans: If a number is divisible by 3 then the sum of digits of this number is divisible by 3.
9. Write the antecedent (given part) and the consequent (part to be proved) in the following statements.
(i) If all sides of a triangle are congruent then it’s all angles are congruent.
Ans:
Given:
In ∆ABC,
side AB ≅ side BC ≅ side AC
To prove:
∠A ≅ ∠B ≅ ∠C
(ii) The diagonals of a parallelogram bisect each other.
Ans:
Given:
□PQRS is a parallelogram
Diagonals PR and QS intersect at point M
To prove:
(a) PM = RM
(b) QM = SM
10*. Draw a labelled figure showing information in each of the following statements and write the antecedent and the consequent.
(i) Two equilateral triangles are similar.
Ans:
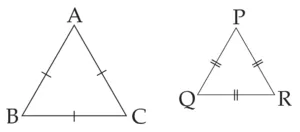
Given:
In ∆ABC,
side AB ≅ side BC ≅ side AC
In ∆PQR,
side PQ ≅ side QR ≅ side PR
To prove:
∆ABC ~ ∆PQR
(ii) If angles in a linear pair are congruent then each of them is a right angle.
Ans:
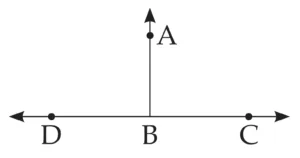
Given:
∠ABC and ∠ABD form a linear pair
∠ABC ≅ ∠ABD
To prove:
∠ABC = ∠ABD = 90º
(iii) If the altitudes drawn on two sides of a triangle are congruent then those two sides are congruent.
Ans:
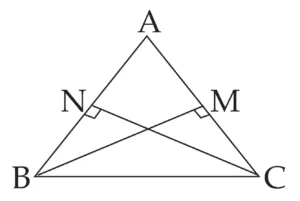
Given:
In ∆ABC,
seg BM ⊥ side AC, A – M – C
seg CN ⊥ side AB, A – N – B
seg BM ≅ seg CN
To prove:
side AB ≅ side AC.
