Chapter 17 – Circle : Chord and Arc
Practice set 17.1
1. In a circle with centre P, chord AB is drawn of length 13 cm, seg PQ ⟂ chord AB, then find l(QB).
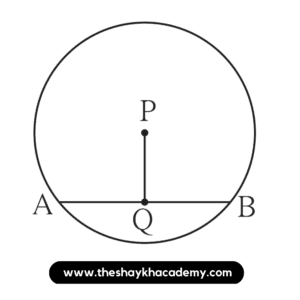
Given:
In a circle with centre P,
l(AB) = 13 cm
seg PQ ⟂ chord AB
To find:
l(QB)
Solution:
We know that the perpendicular drawn from the centre of the circle to the chord bisects the chord.
∴ l(QB) = \(\large \frac {1}{2}\) × l(AB)
∴ l(QB) = \(\large \frac {1}{2}\) × 13
∴ l(QB) = 6.5 cm
Ans: l(QB) = 6.5 cm
2. Radius of a circle with centre O is 25 cm. Find the distance of a chord from the centre if the length of the chord is 48 cm.
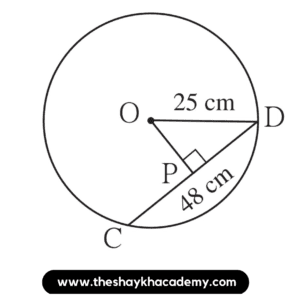
Given:
In a circle with centre O,
l(OD) = 25 cm
l(CD) = 48 cm
To find:
l(OP)
Solution:
We know that the perpendicular drawn from the centre of the circle to the chord bisects the chord.
∴ l(PD) = \(\large \frac {1}{2}\) × l(CD)
∴ l(PD) = \(\large \frac {1}{2}\) × 48
∴ l(PD) = 24 cm
In △OPD,
∠OPD = 90° …[Given]
∴ OD² = OP² + PD² …[By Pythagoras theorem]
∴ 25² = OP² + 24²
∴ 625 = OP² + 576
∴ 625 – 576 = OP²
∴ OP² = 49
∴ \( \sqrt {OP²}\) = \( \sqrt {49}\) …[By Taking square root of both sides]
∴ OP = 7 cm
Ans: Distance of the chord from the centre of the circle is 7 cm.
3. O is the centre of the circle. Find the length of radius, if the chord of length 24 cm is at a distance of 9 cm from the centre of the circle.
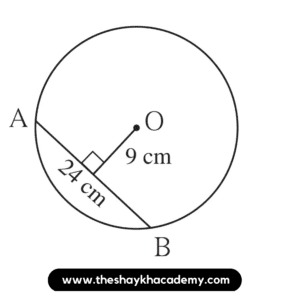
Given:
In a circle with centre O,
l(AB) = 10 cm
Distance of chord from the centre of the circle = 9 cm
To find:
Radius
Solution:
Join seg OA which is the radius of the circle.
We know that the perpendicular drawn from the centre of the circle to the chord bisects the chord.
∴ l(AM) = \(\large \frac {1}{2}\) × l(AB)
∴ l(AM) = \(\large \frac {1}{2}\) × 24
∴ l(AM) = 12 cm
In △OMA,
∠OMA = 90° …[Given]
∴ OA² = OM² + AM² …[By Pythagoras theorem]
∴ OA² = 9² + 12²
∴ OA² = 81 + 144
∴ OA² = 225
∴ \( \sqrt {OA²}\) = \( \sqrt {225}\) …[By Taking square root of both sides]
∴ OP = 15 cm
Ans: Radius of the circle is 15 cm.
4. C is the centre of the circle whose radius is 10 cm. Find the distance of the chord from the centre if the length of the chord is 12 cm.
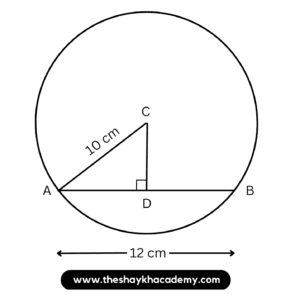
Given:
In a circle with centre C,
Radius = 10 cm
Chord = 12 cm
To find:
Distance of chord from the centre of the circle
Solution:
Let seg AB be the chord of the circle with centre C.
Draw seg CD ⊥ chord AB.
We know that the perpendicular drawn from the centre of the circle to the chord bisects the chord.
∴ l(AD) = \(\large \frac {1}{2}\) × l(AB)
∴ l(AD) = \(\large \frac {1}{2}\) × 12
∴ l(AD) = 6 cm
In △ADC,
∠ADC = 90° …[Given]
∴ AC² = AD² + DC² …[By Pythagoras theorem]
∴ 10² = 6² + DC²
∴ 100 = 36 + DC²
∴ 100 – 36 = DC²
∴ DC² = 64
∴ \( \sqrt {DC²}\) = \( \sqrt {64}\) …[By Taking square root of both sides]
∴ DC = 8 cm
Ans: Distance of the chord from the centre of the circle is 8 cm.
Practice set 17.2
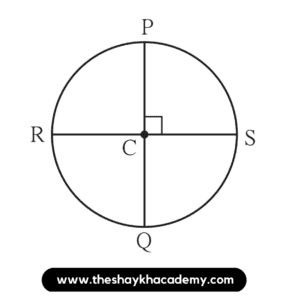
1. The diameters PQ and RS of the circle with centre C are perpendicular to each other at C. State, why arc PS and arc SQ are congruent. Write the other arcs which are congruent to arc PS.
Given:
In a circle with centre C,
Diameter PQ ⊥ Diameter RS
To find:
Why arc PS ≅ arc SQ
Other arcs which are congruent to arc PS
Solution:
Diameter PQ ⊥ Diameter RS …[Given]
∴ m∠PCS = m∠SCQ = m∠PCR = m∠RCQ = 90°
We know that the measure of the angle subtended at the centre by an arc is the measure of the arc.
∴ m∠PCS = m(arc PS)
∵ m∠PCS = 90°
∴ m(arc PS) = 90° …(i)
∴ m∠SCQ = m(arc SQ)
∵ m∠SCQ = 90°
∴ m(arc SQ) = 90°
From (i) and (ii)
∴ m(arc PS) ≅ m(arc SQ) …[If the measures of two arcs of a circle are same, then the two arcs are congruent]
Now,
∴ m∠PCR = m(arc PR)
∵ m∠PCR = 90°
∴ m(arc PR) = 90° …(iii)
∴ m∠RCQ = m(arc RQ)
∵ m∠RCQ = 90°
∴ m(arc RQ) = 90° …(iv)
From (i), (ii), (iii) and (iv)
arc PS ≅ arc PR ≅ arc RQ ≅ arc SQ …[If the measures of two arcs of a circle are same, then the two arcs are congruent]
Ans: arc PS ≅ arc PR ≅ arc RQ ≅ arc SQ
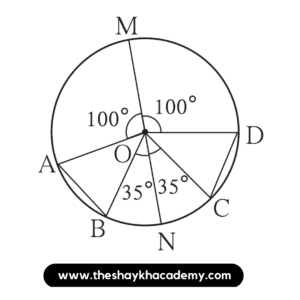
2. In the adjoining figure O is the centre of the circle whose diameter is MN. Measures of some central angles are given in the figure. Hence find the following
(1) m ∠AOB and m ∠COD
(2) Show that arc AB ≅ arc CD.
(3) Show that chord AB ≅ chord CD
Given:
In a circle with centre O,
MN is the diameter
m∠AOM = 100⁰
m∠MOD = 100⁰
m∠BON = 35⁰
m∠NOC = 35⁰
To find:
m∠AOB and m∠COD
To prove:
arc AB ≅ arc CD
chord AB ≅ chord CD
Solution:
m∠AOM + m∠AON = 180° …[Angles in a linear pair]
∴ m∠AOM + (m∠AOB + m∠BON) = 180° …[Angle addition property]
∴ 100° + m∠AOB + 35° = 180° …[Given]
∴ m∠AOB + 135° = 180°
∴ m∠AOB = 180° – 135°
∴ m∠AOB = 45° …(i)
Also,
m∠DOM + m∠DON = 180° …[Angles in a linear pair]
∴ m∠DOM + (m∠COD + m∠CON) = 180° …[Angle addition property]
∴ 100° + m∠COD + 35° = 180° …[Given]
∴ m∠COD + 135° = 180°
∴ m∠COD = 180° – 135°
∴ m∠COD = 45° …(ii)
Now,
∴ m∠AOB = m(arc AB)
∵ m∠AOB = 90°
∴ m(arc AB) = 90° …(iii)
∴ m∠DOC = m(arc DC)
∵ m∠DOC = 90°
∴ m(arc DC) = 90° …(iv)
∴ m(arc AB) = m(arc DC) …[From (iii) and (iv)]
∴ arc AB ≅ arc CD …[If the measures of two arcs of a circle are same, then the two arcs are congruent]
And,
chord AB ≅ chord CD ….[The chords corresponding to congruent arcs are congruent]
Hence Proved
Ans: m∠AOB = 45° and m∠COD = 45°.
