Chapter 15 - Area
Practice set 15.1
1. If the base of a parallelogram is 18 cm and its height is 11 cm, find its area.

Given:
Base of the parallelogram = 18 cm
Height of the parallelogram = 11 cm
To find:
Area of parallelogram
Solution:
Area of parallelogram = Base × Height
∴ Area of parallelogram = 18 × 11
∴ Area of parallelogram = 198 sq.cm
Ans: Area of parallelogram is 198 sq.cm
2. If the area of a parallelogram is 29.6 sq cm and its base is 8 cm, find its height.

Given:
Area of the parallelogram = 29.6 sq cm
Base of the parallelogram = 8 cm
To find:
Height of the parallelogram
Solution:
Area of parallelogram = Base × Height
∴ 29.6 = 8 × Height
∴ \(\large \frac {29.6}{8}\) = Height
∴ Height = 3.7 cm
Ans: Height of the parallelogram is 3.7 cm
3. Area of a parallelogram is 83.2 sq cm. If its height is 6.4 cm, find the length of its base.

Given:
Area of the parallelogram = 83.2 sq cm
Height of the parallelogram = 6.4 cm
To find:
Base of the parallelogram
Solution:
Area of parallelogram = Base × Height
∴ 83.2 = Base × 6.4
∴ \(\large \frac {83.2}{6.4}\) = Base
∴ Base = 13 cm
Ans: Base of the parallelogram is 13 cm
Practice set 15.2
1. Lengths of the diagonals of a rhombus are 15 cm and 24 cm, find its area.

Given:
Length of 1st diagonal = 15 cm
Length of 2nd diagonal = 24 cm
To find:
Area of rhombus
Solution:
Area of rhombus = \(\large \frac {1}{2}\) × Product of diagonals
∴ Area of rhombus = \(\large \frac {1}{2}\) × 15 × 24
∴ Area of rhombus = 15 × 12
∴ Area of rhombus = 180 sq.cm
Ans: Area of rhombus is 180 sq.cm
2. Lengths of the diagonals of a rhombus are 16.5 cm and 14.2 cm, find its area.

Given:
Length of 1st diagonal = 16.5 cm
Length of 2nd diagonal = 14.2 cm
To find:
Area of rhombus
Solution:
Area of rhombus = \(\large \frac {1}{2}\) × Product of diagonals
∴ Area of rhombus = \(\large \frac {1}{2}\) × 16.5 × 14.2
∴ Area of rhombus = 16.5 × 7.1
∴ Area of rhombus = 117.15 sq.cm
Ans: Area of rhombus is 117.15 sq.cm
3. If perimeter of a rhombus is 100 cm and length of one diagonal is 48 cm, what is the area of the quadrilateral?

Given:
Perimeter of rhombus = 100 cm
Length of one diagonal = 48 cm
To find:
Area of rhombus
Solution:
Let □ ABCD be the rhombus with perimeter 100 cm.
Diagonal AC and BD intersect at point M.
We know that,
Perimeter of a rhombus = 4 × side
∴ 100 = 4 × side
∴ \(\large \frac {100}{4}\) = Side
∴ Side = 25 cm
i.e. AB = 25 cm
Also,
Diagonals of a rhombus are perpendicular bisectors of each other
BD = 48 cm …[Given]
∴ BM = \(\large \frac {1}{2}\) × BD
∴ BM = \(\large \frac {1}{2}\) × 25
∴ BM = \(\large \frac {1}{2}\) × 25
In ∆ AMB, ∠ AMB = 90⁰
∴ ∆ AMB is a right angled triangle
∴ AB² = AM² + BM² …[By applying Pythagoras Theorem]
∴ 25² = AM² + 24²
∴ 625 = AM² + 576
∴ 625 – 576 = AM²
∴ AM² = 49
∴ \( \sqrt {AM²}\) = \( \sqrt {49}\) …[By Taking square root of both sides]
∴ AM = 7 cm
Now,
AC = 2 × AM
∴ AC = 2 × 7
∴ AC = 14 cm
Area of rhombus = \(\large \frac {1}{2}\) × Product of diagonals
∴ Area of rhombus = \(\large \frac {1}{2}\) × AC × BD
∴ Area of rhombus = \(\large \frac {1}{2}\) × 14 × 48
∴ Area of rhombus = 14 × 24
∴ Area of rhombus = 336 sq.cm
Ans: Area of rhombus is 336 sq.cm
4*. If length of a diagonal of a rhombus is 30 cm and its area is 240 sq cm, find its perimeter.

Given:
Length of one diagonal = 30 cm
Area of rhombus = 240 sq.cm
To find:
Perimeter of rhombus
Solution:
Let □ PQRS be the rhombus.
Diagonal PR and QS intersect at point M.
Area of rhombus = \(\large \frac {1}{2}\) × Product of diagonals
∴ 240 = \(\large \frac {1}{2}\) × PR × QS
∴ 240 = \(\large \frac {1}{2}\) × 30 × QS
∴ 240 = 15 × QS
∴ \(\large \frac {240}{15}\) = QS
∴ QS = 16 sq.cm
We know that,
Diagonals of a rhombus are perpendicular bisectors of each other
∴ PM = \(\large \frac {1}{2}\) × RP
∴ PM = \(\large \frac {1}{2}\) × 30
∴ PM = 15 cm
and QM = \(\large \frac {1}{2}\) × QS
∴ QM = \(\large \frac {1}{2}\) × 16
∴ QM = 8 cm
In ∆ PMQ, ∠ PMQ = 90⁰
∴ ∆ PMQ is a right angled triangle
∴ PQ² = PM² + QM² …[By applying Pythagoras Theorem]
∴ PQ² = 15² + 8²
∴ PQ² = 225 + 64
∴ PQ² = 289
∴ \( \sqrt {PQ²}\) = \( \sqrt {289}\) …[By Taking square root of both sides]
∴ PQ = 17 cm
Now,
Perimeter of a rhombus = 4 × PQ
∴ Perimeter of a rhombus = 4 × 17
∴ Perimeter of a rhombus = 68 cm
Ans: Perimeter of a rhombus is 68 cm
Practice set 15.3
1. In □ABCD, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area of □ABCD.
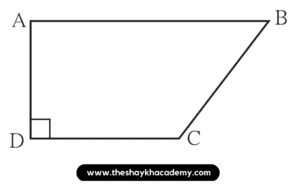
Given:
In □ABCD,
l(AB) = 13 cm
l(DC) = 9 cm
l(AD) = 8 cm
To find:
Area of □ABCD
Solution:
Area of □ABCD = \(\large \frac {1}{2}\) × Sum of parallel sides × Height
∴ Area of □ABCD = \(\large \frac {1}{2}\) × (AB + CD) × AD
∴ Area of □ABCD = \(\large \frac {1}{2}\) × (13 + 9) × 8
∴ Area of □ABCD = 22 × 4
∴ Area of □ABCD = 88 sq.cm
Ans: Area of □ABCD is 88 sq.cm
2. Length of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm respectively and its height is 4.2 cm, find its area.

Given:
Parallel side 1 = 8.5 cm
Parallel side 2 = 11.5 cm
Height of the trapezium = 4.2 cm
To find:
Area of trapezium
Solution:
Area of trapezium = \(\large \frac {1}{2}\) × Sum of parallel sides × Height
∴ Area of trapezium = \(\large \frac {1}{2}\) × (8.5 + 11.5) × 4.2
∴ Area of trapezium = 20 × 2.1
∴ Area of trapezium = 42 sq.cm
Ans: Area of trapezium is 42 sq.cm
3*. □PQRS is an isosceles trapezium l(PQ) = 7 cm. seg PM ⊥ seg SR, l(SM) = 3 cm, Distance between two parallel sides is 4 cm, find the area of □PQRS.

Given:
□PQRS is an isosceles trapezium,
l(PQ) = 7 cm
seg PM ⊥ seg SR
l(SM) = 3 cm
Distance between two parallel sides = 4 cm
To find:
Area of □PQRS
Solution:
In ∆ PMS, ∠ PMS = 90⁰
∴ ∆ AMB is a right angled triangle
∴ PS² = PM² + SM² …[By applying Pythagoras Theorem]
∴ PS² = 3² + 4²
∴ PS² = 9 + 16
∴ PS² = 25
∴ \( \sqrt {PS²}\) = \( \sqrt {25}\) …[By Taking square root of both sides]
∴ PS = 5 cm
PS = QR [∵ □PQRS is an isosceles trapezium]
∴ QR = 5 cm
Draw seg QM ⊥ seg RS such that point N lies on seg RS
∴ QN = PM [Distance between two parallel lines are same.]
∴ QN = 4 cm
In ∆ QNR, ∠ QNR = 90⁰
∴ ∆ QNR is a right angled triangle
∴ QR² = QN² + RN² …[By applying Pythagoras Theorem]
∴ 5² = 4² + RN²
∴ 25 = 16 + RN²
∴ 25 – 16 = RN²
∴ RN² = 9
∴ \( \sqrt {RN²}\) = \( \sqrt {9}\) …[By Taking square root of both sides]
∴ RN = 3 cm
In □PMNQ,
PM || QN [∵ They are ⊥ to the same line]
∴ PQ || MN [Parts of parallel sides]
∴ □PMNQ is a parallelogram.
∴ MN = PQ [Opposite sides of parallelogram are congruent]
∴ MN = 7 cm
Now,
SR = SM + MN + NR
∴ SR = 3 + 7 + 3
∴ SR = 13 cm
Area of □PQRS = \(\large \frac {1}{2}\) × Sum of parallel sides × Height
∴ Area of □PQRS = \(\large \frac {1}{2}\) × (PQ + RS) × PM
∴ Area of □PQRS = \(\large \frac {1}{2}\) × (7 + 13) × 4
∴ Area of □PQRS = 20 × 2
∴ Area of □PQRS = 40 sq.cm
Ans: Area of trapezium is 40 sq.cm
Practice set 15.4
1. Sides of a triangle are 45 cm, 39 cm and 42 cm, find its area.

Given:
a = 45 cm
b = 39 cm
c = 42 cm
To find:
Area of triangle
Solution:
We know that,
semiperimeter (s) = \(\large \frac {a\, +\, b\, +\, c}{2}\)
∴ s = \(\large \frac {45\, +\, 39\, +\, 42}{2}\)
∴ s = \(\large \frac {126}{2}\)
∴ s = 63
Area of triangle = \( \sqrt {s\, (s\, –\, a)(s\, –\, b)(s\, –\, c) }\)
∴ Area of triangle = \( \sqrt {63\, (63\, –\, 45)(63\, –\, 39)(63\, –\, 42) }\)
∴ Area of triangle = \( \sqrt {63\, ×\, 18\, ×\, 24\, ×\, 21) }\)
∴ Area of triangle = \( \sqrt {9\, ×\, 7\, ×\, 2\, ×\, 9\, ×\, 2\, ×\, 4\, ×\, 3\, ×\, 3\, ×\, 7) }\)
∴ Area of triangle = \( \sqrt {9²\, ×\, 7²\, ×\, 2²\, ×\, 2²\, ×\, 3²) }\)
∴ Area of triangle = 9 × 7 × 2 × 2 ×3
∴ Area of triangle = 756 sq.cm
Ans: Area of triangle is 756 sq.cm
2. Look at the measures shown in the adjacent figure and find the area of □PQRS.

Given:
PS = 36 m
SR = 15 m
PQ = 56 m
QR = 25 m
∠ PSR = 90⁰
To find:
Area of □PQRS
Solution:
In ∆ PSR, ∠ PSR = 90⁰
∴ ∆ PSR is a right angled triangle
∴ PR² = PS² + SR² …[By applying Pythagoras Theorem]
∴ PR² = 36² + 15²
∴ PR² = 1296 + 225
∴ PR² = 1521
∴ \( \sqrt {PR²}\) = \( \sqrt {1521}\) …[By Taking square root of both sides]
∴ PR = 39 m
Area of ∆PSR = \(\large \frac {1}{2}\) × Base × Height
∴ Area of ∆PSR = \(\large \frac {1}{2}\) × SR × PS
∴ Area of ∆PSR = \(\large \frac {1}{2}\) × 15 × 36
∴ Area of ∆PSR = 15 × 18
∴ Area of ∆PSR = 270 sq.m …(i)
For ∆PQR,
semiperimeter (s) = \(\large \frac {a\, +\, b\, +\, c}{2}\)
∴ s = \(\large \frac {39\, +\, 25\, +\, 56}{2}\)
∴ s = \(\large \frac {120}{2}\)
∴ s = 60
Area of ∆PQR = \( \sqrt {s\, (s\, –\, a)(s\, –\, b)(s\, –\, c) }\)
∴ Area of ∆PQR = \( \sqrt {60\, (60\, –\, 39)(60\, –\, 25)(60\, –\, 56) }\)
∴ Area of ∆PQR = \( \sqrt {60\, ×\, 21\, ×\, 35\, ×\, 4) }\)
∴ Area of ∆PQR = \( \sqrt {4\, ×\, 5\, ×\, 3\, ×\, 3\, ×\, 7\, ×\, 7\, ×\, 5\, ×\, 4) }\)
∴ Area of ∆PQR = \( \sqrt {4²\, ×\, 5²\, ×\, 3²\, ×\, 7²) }\)
∴ Area of ∆PQR = 4 × 5 × 3 × 7
∴ Area of ∆PQR = 420 sq.m …(ii)
Now,
Area of □PQRS = Area of ∆PSR + Area of ∆PQR
∴ Area of □PQRS = 270 + 420 …[From (i) and (ii)]
∴ Area of □PQRS = 690 sq.m
Ans: Area of □PQRS is 690 sq.m
3. Some measures are given in the adjacent figure, find the area of □ABCD.

Given:
AD = 9 m
AB = 40 m
BE = 13 m
DC = 60 m
∠ BAD = 90⁰
∠ BEC = 90⁰
To find:
Area of □ABCD
Solution:
Area of ∆BAD = \(\large \frac {1}{2}\) × Base × Height
∴ Area of ∆BAD = \(\large \frac {1}{2}\) × AD × AB
∴ Area of ∆BAD = \(\large \frac {1}{2}\) × 9 × 40
∴ Area of ∆BAD = 9 × 20
∴ Area of ∆BAD = 180 sq.m …(i)
Area of ∆BCD = \(\large \frac {1}{2}\) × Base × Height
∴ Area of ∆BCD = \(\large \frac {1}{2}\) × DC × BE
∴ Area of ∆BCD = \(\large \frac {1}{2}\) × 60 × 13
∴ Area of ∆BCD = 30 × 13
∴ Area of ∆BCD = 390 sq.m …(ii)
Now,
Area of □ABCD = Area of ∆BAD + Area of ∆BCD
∴ Area of □ABCD = 180 + 390 …[From (i) and (ii)]
∴ Area of □ABCD = 570 sq.m
Ans: Area of □ABCD is 570 sq.m
Practice set 15.5
Find the areas of given plots. (All measures are in metres.)
1.

Given:
AP = 30
QA = 50
AB = 30
BC = 30
RC = 25
CS = 60
BT = 30
To find:
Area of the given plot
Solution:
Area of ∆PAQ = \(\large \frac {1}{2}\) × Base × Height
∴ Area of ∆PAQ = \(\large \frac {1}{2}\) × PA × QA
∴ Area of ∆PAQ = \(\large \frac {1}{2}\) × 30 × 50
∴ Area of ∆PAQ = 30 × 25
∴ Area of ∆PAQ = 750 sq.m …(i)
Area of ∆RCS = \(\large \frac {1}{2}\) × Base × Height
∴ Area of ∆RCS = \(\large \frac {1}{2}\) × CS × RC
∴ Area of ∆RCS = \(\large \frac {1}{2}\) × 60 × 25
∴ Area of ∆RCS = 30 × 25
∴ Area of ∆RCS = 750 sq.m …(ii)
Area of ∆PTS = \(\large \frac {1}{2}\) × Base × Height
∴ Area of ∆PTS = \(\large \frac {1}{2}\) × PS × TB
∴ Area of ∆PTS = \(\large \frac {1}{2}\) × 150 × 30
∴ Area of ∆PTS = 75 × 30
∴ Area of ∆PTS = 2250 sq.m …(iii)
□QRCA is a trapezium
Area of □QRCA = \(\large \frac {1}{2}\) × Sum of parallel sides × Height
∴ Area of □QRCA = \(\large \frac {1}{2}\) × (AQ + CR) × AC
∴ Area of □QRCA = \(\large \frac {1}{2}\) × (50 + 25) × 60
∴ Area of □QRCA = 75 × 30
∴ Area of □QRCA = 2250 sq.cm …(iv)
Now,
Area of the given plot = Area of ∆PAQ + Area of ∆RCS + Area of ∆PTS + Area of □QRCA
∴ Area of the given plot = 750 + 750 + 2250 + 2250
∴ Area of the given plot = 6000 sq.m
Ans: Area of the given plot is 6000 sq.m
2.

Given:
AB = 24
BC = 26
BE = 30
CE = 28
FD = 16
∠ BAE = 90⁰
To find:
Area of the given plot
Solution:
In ∆ BAE, ∠ BAE = 90⁰
∴ ∆ BAE is a right angled triangle
∴ BE² = BA² + AE² …[By applying Pythagoras Theorem]
∴ 30² = 24² + AE²
∴ 900 = 576 + AE²
∴ 900 – 576 = AE²
∴ AE² = 324
∴ \( \sqrt {AE²}\) = \( \sqrt {324}\) …[By Taking square root of both sides]
∴ AE = 18 m
Area of ∆ABE = \(\large \frac {1}{2}\) × Base × Height
∴ Area of ∆ABE = \(\large \frac {1}{2}\) × AB × AE
∴ Area of ∆ABE = \(\large \frac {1}{2}\) × 24 × 18
∴ Area of ∆ABE = 24 × 9
∴ Area of ∆ABE = 216 sq.m …(i)
Area of ∆CDE = \(\large \frac {1}{2}\) × Base × Height
∴ Area of ∆CDE = \(\large \frac {1}{2}\) × CE × DF
∴ Area of ∆CDE = \(\large \frac {1}{2}\) × 28 × 16
∴ Area of ∆CDE = 28 × 8
∴ Area of ∆CDE = 224 sq.m …(ii)
For ∆BCE,
semiperimeter (s) = \(\large \frac {a\, +\, b\, +\, c}{2}\)
∴ s = \(\large \frac {26\, +\, 30\, +\, 28}{2}\)
∴ s = \(\large \frac {84}{2}\)
∴ s = 42
Area of ∆BCE = \( \sqrt {s\, (s\, –\, a)(s\, –\, b)(s\, –\, c) }\)
∴ Area of ∆BCE = \( \sqrt {42\, (42\, –\, 26)(42\, –\, 30)(42\, –\, 28) }\)
∴ Area of ∆BCE = \( \sqrt {42\, ×\, 16\, ×\, 12\, ×\, 14) }\)
∴ Area of ∆BCE = \( \sqrt {7\, ×\, 6\, ×\, 4\, ×\, 4\, ×\, 6\, ×\, 2\, ×\, 2\, ×\, 7) }\)
∴ Area of ∆BCE = \( \sqrt {7²\, ×\, 6²\, ×\, 4²\, ×\, 2²) }\)
∴ Area of ∆BCE = 7 × 6 × 4 × 2
∴ Area of ∆BCE = 336 sq.m …(iii)
Now,
Area of the given plot = Area of ∆ABE + Area of ∆CDE + Area of ∆BCE
∴ Area of the given plot = 216 + 224 + 336
∴ Area of the given plot = 776 sq.m
Ans: Area of the given plot is 776 sq.m
Practice set 15.6
1. Radii of the circles are given below, find their areas.
(1) 28 cm

Given:
Radius of the circle = 28 cm
To find:
Area of the circle
Solution:
Area of the circle = πr²
∴ Area of the circle = \(\large \frac {22}{7}\) × 28 × 28
∴ Area of the circle = 22 × 4 × 28
∴ Area of the circle = 2464 sq.cm
Ans: Area of the circle is 2464 sq.cm
(2) 10.5 cm

Given:
Radius of the circle = 10.5 cm
To find:
Area of the circle
Solution:
Area of the circle = πr²
∴ Area of the circle = \(\large \frac {22}{7}\) × 10.5 × 10.5
∴ Area of the circle = 22 × 1.5 × 10.5
∴ Area of the circle = 346.5 sq.cm
Ans: Area of the circle is 346.5 sq.cm
(3) 17.5 cm

Given:
Radius of the circle = 17.5 cm
To find:
Area of the circle
Solution:
Area of the circle = πr²
∴ Area of the circle = \(\large \frac {22}{7}\) × 17.5 × 17.5
∴ Area of the circle = 22 × 2.5 × 17.5
∴ Area of the circle = 962.5 sq.cm
Ans: Area of the circle = 962.5 sq.cm
2. Areas of some circles are given below, find their diameters.
(1) 176 sq cm

Given:
Area of the circle = 176 sq cm
To find:
Diameter of the circle
Solution:
Area of the circle = πr²
∴ 176 = \(\large \frac {22}{7}\) × r²
∴ \(\large \frac {176\, ×\, 7}{22}\) = r²
∴ r² = 56
∴ \( \sqrt {r²}\) = \( \sqrt {56}\) …[By Taking square root of both sides]
∴ r = \( \sqrt {56}\) m
Diameter of the circle = 2 × radius
∴ Diameter of the circle = 2 × \( \sqrt {56}\)
∴ Diameter of the circle = 2\( \sqrt {56}\) m
Ans: Diameter of the circle = 2\( \sqrt {56}\) m
(2) 394.24 sq cm

Given:
Area of the circle = 394.24 sq cm
To find:
Diameter of the circle
Solution:
Area of the circle = πr²
∴ 394.24 = \(\large \frac {22}{7}\) × r²
∴ \(\large \frac {394.24\, ×\, 7}{22}\) = r²
∴ r² = 17.92 × 7
∴ r² = 125.44
∴ \( \sqrt {r²}\) = \( \sqrt {125.44}\) …[By Taking square root of both sides]
∴ r = 11.2 m
Diameter of the circle = 2 × radius
∴ Diameter of the circle = 2 × 11.2
∴ Diameter of the circle = 22.4 m
Ans: Diameter of the circle is 22.4 m
(3) 12474 sq cm

Given:
Area of the circle = 12474 sq cm
To find:
Diameter of the circle
Solution:
Area of the circle = πr²
∴ 12474 = \(\large \frac {22}{7}\) × r²
∴ \(\large \frac {12474\, ×\, 7}{22}\) = r²
∴ r² = 567 × 7
∴ r² = 3969
∴ \( \sqrt {r²}\) = \( \sqrt {3969}\) …[By Taking square root of both sides]
∴ r = 63 m
Diameter of the circle = 2 × radius
∴ Diameter of the circle = 2 × 63
∴ Diameter of the circle = 126 m
Ans: Diameter of the circle = 126 m
3. Diameter of the circular garden is 42 m. There is a 3.5 m wide road around the garden. Find the area of the road.

Given:
Diameter of the circular garden = 42 m
Width of the road = 3.5 m
To find:
Area of the road
Solution:
Diameter of the circular garden = 42 m
∴ Radius of the circular garden = \(\large \frac {42}{2}\)
∴ Radius of the circular garden = 21 m
Area of the circular garden = πr²
∴ Area of the circular garden = \(\large \frac {22}{7}\) × 21 × 21
∴ Area of the circular garden = 22 × 21 × 3
∴ Area of the circular garden = 1386 sq.cm
Now,
Width of the road = 3.5 m
Outer Radius = Radius of the circular garden + Width of the road
∴ Outer Radius = 21 + 3.5
∴ Outer Radius = 24.5
Area of the outer circle = πr²
∴ Area of the outer circle = \(\large \frac {22}{7}\) × 24.5 × 24.5
∴ Area of the outer circle = 22 × 24.5 × 3.5
∴ Area of the outer circle = 1886.5 sq.cm
Area of the road = Area of the outer circle – Area of the circular garden
∴ Area of the road = 1886.5 – 1386
∴ Area of the road = 500.5 sq.m
Ans: Area of the road is 500.5 sq.m
4. Find the area of the circle if its circumference is 88 cm.

Given:
Circumference of the circle = 88 cm
To find:
Area of the circle
Solution:
We know that,
Circumference of the circle = 2πr
∴ 88 = 2 × \(\large \frac {22}{7}\) × r
∴ 88 = \(\large \frac {44}{7}\) × r
∴ \(\large \frac {88\, ×\, 7}{44}\) = r
∴ r = 2 × 7
∴ r = 14 cm
Now,
Area of the circle = πr²
∴ Area of the circle = \(\large \frac {22}{7}\) × 14 × 14
∴ Area of the circle = 22 × 14 × 2
∴ Area of the circle = 616 sq.cm
Ans: Area of the circle is 616 sq.cm
