Chapter 13 - Congruence of triangles
Practice set 13.1
1. In each pair of triangles in the following figures, parts bearing identical marks are congruent. State the test and correspondence of vertices by which triangles in each pair are congruent.
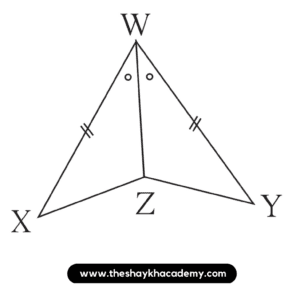
(i)
Solution:
In ∆XWZ and ∆YWZ,
Side WX ≅ Side WY …[Given]
∠XWZ ≅ ∠YWZ …[Given]
Side WZ ≅ Side WZ …[Common side]
∴ ∆XWZ ≅ ∆YWZ by SAS Test in the correspondence XWZ ↔ YWZ.
(ii)
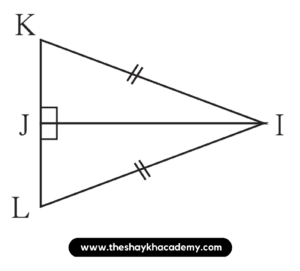
Solution:
The given triangles are right angled triangles.
In ∆KJI and ∆LJI,
Hypotenuse IK ≅ Hypotenuse IL …[Given]
Side IJ ≅ Side IJ …[Common side]
∴ ∆KJI ≅ ∆LJI by hypotenuse-side test in the correspondence KJI ↔ LJI.
(iii)
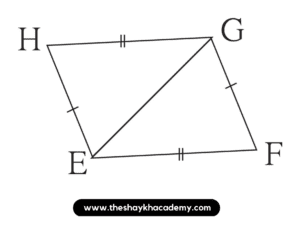
Solution:
In ∆HEG and ∆FGE,
Side HE ≅ Side GF …[Given]
Side HG ≅ Side EF …[Given]
Side EG ≅ Side EG …[Common side]
∴ ∆HEG ≅ ∆FGE by SSS test in the correspondence HEG ↔ FGE.
(iv)
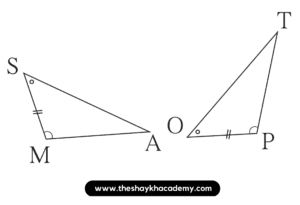
Solution:
In ∆SMA and ∆OPT,
∠ASM ≅ ∠TOP …[Given]
Side SM ≅ Side OP …[Given]
∠SMA ≅ ∠OPT …[Given]
∴ ∆SMA ≅ ∆OPT by ASA test is the correspondence SMA ↔ OPT.
(v)
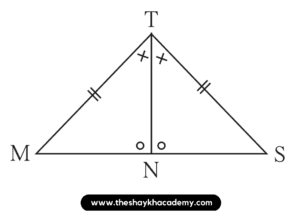
In ∆MTN and ∆STN,
Side MT ≅ Side ST …[Given]
∠MTN ≅ ∠STN …[Given]
∠TNM ≅ ∠TNS …[Given]
∴ ∆MTN ≅ ∆STN by SAA test in the correspondence MTN ↔ STN.
Practice set 13.2
1. In each pair of triangles given below, parts shown by identical marks are congruent. State the test and the one to one correspondence of vertices by which triangles in each pair are congruent and remaining congruent parts.
(i)
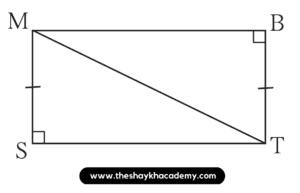
Solution:
In ∆MST and ∆TBM,
∴ side MS ≅ side TB … [Given]
∠MST ≅ ∠TBM …[Given, Both are 90⁰]
Hypotenuse MT ≅ Hypotenuse MT …[Common side]
∴ ∆MST ≅ ∆TBM …[By Hypotenuse-side test]
∴ side ST ≅ side BM …[Corresponding side of congruent triangles]
∠SMT ≅ ∠BTM …[Corresponding angle of congruent triangles]
∠STM ≅ ∠BMT …[Corresponding angle of congruent triangles]
(ii)
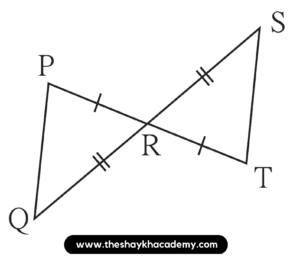
Solution:
In ∆PRQ and ∆TRS,
side PR ≅ side TR … [Given]
∠PRQ ≅ ∠TRS …[Vertically opposite angles]
side RQ ≅ side RS … [Given]
∴ ∆PRQ ≅ ∆TRS …[By SAS test]
∴ side PQ ≅ side TS …[Corresponding side of congruent triangles]
∠RPQ ≅ ∠RTS …[Corresponding angle of congruent triangles]
∠PQR ≅ ∠TSR …[Corresponding angle of congruent triangles]
(iii)
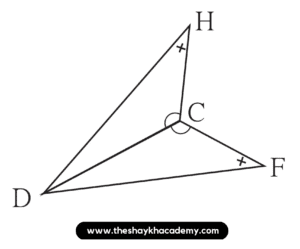
Solution:
In ∆DCH and ∆DCF,
∠DCH ≅ ∠DCF …[Given]
∠DHC ≅ ∠DFC …[Given]
side DC ≅ side DC …[Common side]
∴ ∆DCH ≅ ∆DCF …[By AAS test]
∴ side HC ≅ side FC …[Corresponding side of congruent triangles]
side DH ≅ side DF…[Corresponding side of congruent triangles]
∠HDC ≅ ∠FDC ….[Corresponding angle of congruent triangles]
2*. In the adjacent figure, seg AD ≅ seg EC. Which additional information is needed to show that △ABD and △EBC will be congruent by A-A-S test ?
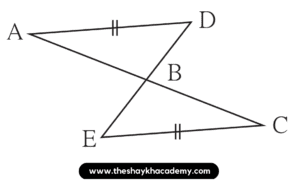
Solution:
In ∆ABD and ∆CBE,
∴ seg AD ≅ seg CE …[Given]
∠ABD ≅ ∠CBE …[Vertically opposite angles]
For the AAS test, 2 conditions are proved and 1 condition of angle remains.
∴ The necessary condition for the two triangles to be congruent by AAS test is
∠ADB ≅ ∠CEB or ∠DAB ≅ ∠ECB
