Theorem of Geometric mean
Theorem :
In a right angled triangle, the perpendicular segment to the hypotenuse from the opposite vertex, is the geometric mean of the segments into which the hypotenuse is divided.
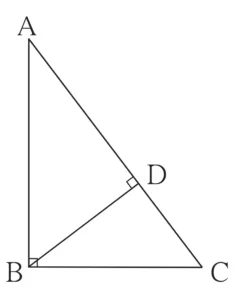
Given :
In ∆ABC,
∠ABC = 90°
seg BD ⊥ seg AC
A – B – C
To prove :
BD² = AD × DC
Proof :
In ∆ADB and ∆ABC
∠DAB ≅ ∠BAC …[Common angle]
∠ADB ≅ ∠ABC …[Both are 90°]
∆ADB ~ ∆ABC …[By AA test of similarity of triangles] (i)
In ∆BDC and ∆ABC
∠BCD ≅ ∠ACB …[Common angle]
∠BDC ≅ ∠ABC …[Both are 90°]
∆BDC ~ ∆ABC …[By AA test of similarity of triangles] (ii)
∴ ∆ADB ~ ∆BDC …[From (i) and (ii)]
∴ \(\large \frac {BD}{DC}\) = \(\large \frac {AD}{BD}\)
∴ BD² = AD × DC
∴ BD is the geometric mean of AD and DC
Hence Proved.
