Theorem of Areas of Similar Triangles
Theorem :
When two triangles are similar, the ratio of areas of those triangles is equal to the ratio of the squares of their corresponding sides.
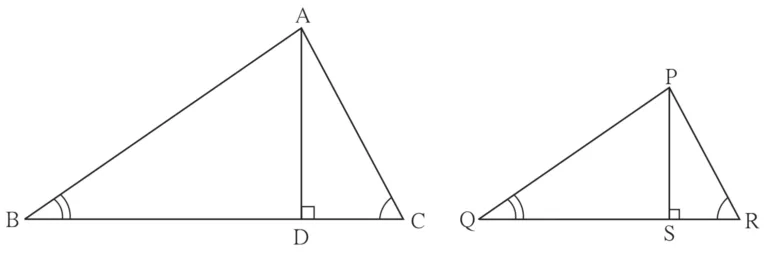
Given :
∆ABC ~ ∆PQR
AD ⊥ BC
PS ⊥ QR
To prove :
\(\large \frac {A(∆ABC)}{A(∆PQR)}\) = \(\large \frac {AB²}{PQ²}\) = \(\large \frac {BC²}{QR²}\) = \(\large \frac {AC²}{PR²}\)
Proof :
\(\large \frac {A(∆ABC)}{A(∆PQR)}\) = \(\large \frac {BC \,×\, AD}{QR \,×\, PS}\)
∴ \(\large \frac {A(∆ABC)}{A(∆PQR)}\) = \(\large \frac {BC}{QR}\) × \(\large \frac {AD}{PS}\) …(i)
In ∆ABD and ∆PQS,
∠B = ∠Q …[Given]
∠ADB ≅ ∠PSQ …[Both are 90⁰]
∴ ∆ABD ~ ∆PQS …[By AA test of similarity of triangles]
∴ \(\large \frac {AD}{PS}\) = \(\large \frac {AB}{PQ}\) …(ii)
But ∆ABC ~ ∆PQR
∴ \(\large \frac {AB}{PQ}\) = \(\large \frac {BC}{PR}\) …(iii)
From (i), (ii) and (ii)
\(\large \frac {A(∆ABC)}{A(∆PQR)}\) = \(\large \frac {BC}{QR}\) × \(\large \frac {AD}{PS}\)
∴ \(\large \frac {A(∆ABC)}{A(∆PQR)}\) = \(\large \frac {BC}{PR}\) × \(\large \frac {BC}{PR}\)
∴ \(\large \frac {A(∆ABC)}{A(∆PQR)}\) = \(\large \frac {BC²}{PR²}\)
Hence Proved.
Similarly, we can prove that,
∴ \(\large \frac {A(∆ABC)}{A(∆PQR)}\) = \(\large \frac {AB²}{PQ²}\)
and
∴ \(\large \frac {A(∆ABC)}{A(∆PQR)}\) = \(\large \frac {AC²}{PR²}\)
