Apollonius Theorem
Theorem :
In ∆ABC, if M is the midpoint of side BC, then AB² + AC² = 2AM² + 2BM²
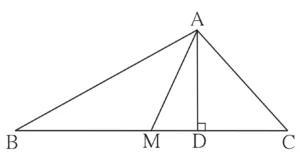
Given :
In ∆ABC,
M is the midpoint of side BC
To prove :
AB² + AC² = 2AM² + 2BM²
Construction :
Draw seg AD ⊥ seg BC
Proof :
In ∆ABD,
∠ABD = 90⁰
∴ AB² = AD² + BD² …[By Pythagoras theorem] (i)
In ∆ADC,
∠ADC = 90⁰
∴ AC² = AD² + DC² …[By Pythagoras theorem] (ii)
In ∆ADM,
∠ADM = 90⁰
∴ AM² = AD² + MD² …[By Pythagoras theorem] (iii)
Adding equations (i) and (ii), we get,
AB² + AC² = AD² + BD² + AD² + DC²
∴ AB² + AC² = 2AD² + BD² + DC²
∴ AB² + AC² = 2AD² + (BM + MD)² + (CM – MD)² …[From figure]
∴ AB² + AC² = 2AD² + (BM + MD)² + (BM – MD)² …[∵ BM = CM]
∴ AB² + AC² = 2AD² + BM² + MD² + 2BM × MD + BM² + MD² – 2BM × MD²
∴ AB² + AC² = 2AD² + BM² + BM²
∴ AB² + AC² = 2AD² + 2 BM² + 2 MD²
∴ AB² + AC² = (2AD² + 2 MD²) + 2 BM²
∴ AB² + AC² = 2(AD² + MD²) + 2 BM²
∴ AB² + AC² = 2AM² + 2 BM² …[From (iii)]
Hence Proved.
