THEOREMS

Angle Bisector Theorem

Theorem : 

The bisector of an angle of a triangle divides the side opposite to the angle in the ratio of the remaining sides.

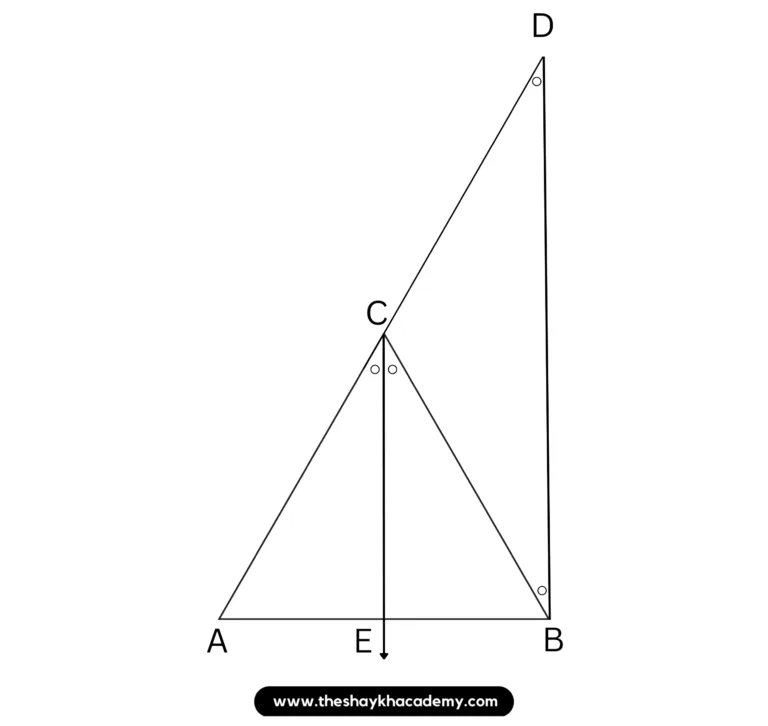
Angle Bisector Theorem

Given :

In ∆ ABC,

Bisector of ∠C intersects seg AB in the point E.

To prove :

\(\large \frac {AE}{EB}\) = \(\large \frac {CA}{CB}\)

Construction: 

Draw a line parallel to ray CE, passing through the point B. Extend AC so as to intersect it at point D.

Proof :

In ∆ ADB,

ray CE || ray BD and AD is transversal,

∴ ∠ACE ≅ ∠CDB … (i) [Corresponding angles]

 

Now,

Taking BC as transversal

∠ECB ≅ ∠CBD … (ii) [Alternate angles] 

 

But

∠ACE ≅ ∠ECB … (iii) (Given)

∴ ∠CBD ≅ ∠CDB … [from (i), (ii) and (iii)]

 

In ∆ CBD, 

side CB ≅ side CD … [sides opposite to congruent angles]

∴ CB = CD … (iv)

 

Now,

In ∆ ABD,

seg EC || seg BD … (Construction)

∴ \(\large \frac {AE}{EB}\) = \(\large \frac {CA}{CD}\) … (v) [Basic proportionality theorem]

 

 ∴ \(\large \frac {AE}{EB}\) = \(\large \frac {CA}{CB}\) … [from (iv) and (v)]

Hence proved