Chapter 6 – Trigonometry
Practice set 6.1
1. If sinθ = \(\large \frac {7}{25}\), find the values of cosθ and tanθ.
Solution:
sinθ = \(\large \frac {7}{25}\)
We know that,
sin²θ + cos²θ = 1
∴ \(\large (\frac {7}{25})\)² + cos²θ = 1
∴ cos²θ = 1 – \(\large \frac {49}{625}\)
∴ cos²θ = \(\large \frac {625\,–\,49}{625}\)
∴ cos²θ = \(\large \frac {576}{625}\)
∴ cosθ = \(\large \frac {24}{25}\) …[Taking square roots]
Now,
tanθ = \(\large \frac {sinθ}{cosθ}\)
∴ tanθ = \(\large \frac {7}{25}\) ÷ \(\large \frac {24}{25}\)
∴ tanθ = \(\large \frac {7}{25}\) × \(\large \frac {25}{24}\)
∴ tanθ = \(\large \frac {7}{24}\)
Ans: cosθ = \(\large \frac {24}{25}\) and tanθ = \(\large \frac {7}{24}\).
2. If tanθ = \(\large \frac {3}{4}\), find the values of secθ and cosθ.
Solution:
tanθ = \(\large \frac {3}{4}\)
We know that,
1 + tan²θ = sec²θ
∴ 1 + \(\large (\frac {3}{4})²\) = sec²θ
∴ 1 + \(\large \frac {9}{16}\) = sec²θ
∴ \(\large \frac {16\,+\,9}{16}\) = sec²θ
∴ sec²θ = \(\large \frac {25}{16}\)
∴ secθ = \(\large \frac {5}{4}\) …[Taking square roots]
Now,
cosθ = \(\large \frac {1}{secθ}\)
∴ cosθ = \(\large \frac {1}{\frac {5}{4}}\)
∴ cosθ = 1 × \(\large \frac {4}{5}\)
∴ cosθ = \(\large \frac {4}{5}\)
Ans: secθ = \(\large \frac {5}{4}\) and cosθ = \(\large \frac {4}{5}\).
3. If cotθ = \(\large \frac {40}{9}\), find the values of cosecθ and sinθ.
Solution:
cotθ = \(\large \frac {40}{9}\)
We know that,
cosec²θ = 1 + cot²θ
∴ cosec²θ = 1 + \(\large (\frac {40}{9})²\)
∴ cosec²θ = 1 + \(\large\frac {1600}{81}\)
∴ cosec²θ = \(\large\frac {81\,+\,1600}{81}\)
∴ cosec²θ = \(\large\frac {1681}{81}\)
∴ cosecθ = \(\large\frac {41}{40}\) …[Taking square roots]
Now,
sinθ = \(\large \frac {1}{cosecθ}\)
∴ sinθ = \(\large \frac {1}{\frac {41}{9}}\)
∴ sinθ = \(\large \frac {9}{41}\)
Ans: cosecθ = \(\large\frac {41}{40}\) and sinθ = \(\large \frac {9}{41}\).
4. If 5secθ – 12cosecθ = 0, find the values of secθ, cosθ and sinθ.
Solution:
5 secθ – 12 cosecθ = 0
∴ 5 secθ = 12 cosecθ
∴ \(\large \frac {5}{cosθ}\) = \(\large \frac {12}{sinθ}\)
∴ \(\large \frac {sinθ}{cosθ}\) = \(\large \frac {12}{5}\)
∴ tanθ = \(\large \frac {12}{5}\)
We know that,
sec²θ = 1 + tan²θ
∴ sec²θ = 1 + \(\large (\frac {12}{5})²\)
∴ sec²θ = 1 + \(\large \frac {144}{25}\)
∴ sec²θ = \(\large \frac {25\,+\,144}{25}\)
∴ sec²θ = \(\large \frac {169}{25}\)
∴ secθ = \(\large \frac {13}{5}\) …[Taking square roots]
Now,
∴ cosθ = \(\large \frac {1}{secθ}\)
∴ cosθ = \(\large \frac {1}{\frac {13}{5}}\)
∴ cosθ = \(\large \frac {5}{13}\)
Also,
tanθ = \(\large \frac {sinθ}{cosθ}\)
∴ sinθ = tanθ × cosθ
∴ sinθ = \(\large \frac {12}{5}\) × \(\large \frac {5}{13}\)
∴ sinθ = \(\large \frac {12}{13}\)
Ans: secθ = \(\large \frac {13}{5}\), cosθ = \(\large \frac {5}{13}\) and sinθ = \(\large \frac {12}{13}\).
5. If tanθ = 1 then, find the values of \(\large \frac {sinθ\,+\,cosθ} {secθ\,+\,cosecθ}\).
Solution:
tanθ = 1 …[Given]
We know that,
sec²θ = 1 + tan²θ
∴ sec²θ = 1 + (1)²
∴ sec²θ = 1 + 1
∴ sec²θ = 2
∴ secθ = \(\sqrt{2}\) …[Taking square root]
cosθ = \(\large \frac {1}{\sqrt{2}}\)
tanθ = 1 …[Given]
∴ \(\large \frac {sinθ}{cosθ}\) = 1
∴ sinθ = cosθ
∴ sinθ = \(\large \frac {1}{\sqrt{2}}\)
cosecθ = \(\large \frac {1}{sinθ}\)
∴ cosecθ = \(\sqrt{2}\)
Now,
\(\large \frac {sinθ\,+\,cosθ}{secθ\,+\,cosecθ}\) = \(\large \frac {\frac{1}{\sqrt{2}}\,+\,\frac {1}{\sqrt{2}}}{\sqrt{2}\,+\,\sqrt{2}}\)
∴ \(\large \frac {sinθ\,+\,cosθ}{secθ\,+\,cosecθ}\) = \(\large \frac {\frac {2}{\sqrt{2}}}{2\sqrt{2}}\)
∴ \(\large \frac {sinθ\,+\,cosθ}{secθ\,+\,cosecθ}\) = \(\large \frac {2}{\sqrt{2}}\) × \(\large \frac {1}{2\sqrt{2}}\)
∴ \(\large \frac {sinθ\,+\,cosθ}{secθ\,+\,cosecθ}\) = \(\large \frac {1}{2}\)
Ans: \(\large \frac {sinθ\,+\,cosθ}{secθ\,+\,cosecθ}\) = \(\large \frac {1}{2}\)
6. Prove that:
(1) \(\large \frac {sin²θ}{cosθ}\) + cosθ = secθ
Proof:
LHS
= \(\large \frac {sin²θ}{cosθ}\) + cosθ
= \(\large \frac {sin²θ\,+\,cos²θ}{cosθ}\)
= \(\large \frac {1}{cosθ}\) …[sin²θ + cos²θ = 1]
= secθ
= R.H.S.
Hence proved.
(2) cos²θ (1 + tan²θ) = 1
Proof:
LHS
= cos²θ (1 + tan²θ)
= cos²θ (sec²θ) …[1 + tan²θ = sec²θ]
= cos²θ × \(\large \frac {1}{cos²θ}\)
= 1
= R.H.S.
Hence proved.
(3) \(\sqrt{\frac {1\,–\,sinθ}{1\,+\,sinθ}}\) = secθ – tanθ
Proof:
LHS
= \(\sqrt{\large \frac {1\,–\,sinθ}{1\,+\,sinθ}}\)
= \(\sqrt{\large \frac {(1\,–\,sinθ)(1\,–\,sinθ)}{(1\,+\,sinθ)(1\,–\,sinθ)}}\)
= \(\sqrt{\large \frac {(1\,–\,sinθ)²}{1\,–\,sin²θ}}\)
= \(\sqrt{\large \frac {(1\,–\,sinθ)²}{cos²θ}}\) …[∵ sin²θ + cos²θ = 1, cos²θ = 1 – sin²θ]
= \(\large \frac {1\,–\,sinθ}{cosθ}\)
= \(\large \frac {1}{cosθ}\) – \(\large \frac {sinθ}{cosθ}\)
= secθ – tanθ
= R.H.S.
Hence proved.
(4) (secθ – cosθ)(cotθ + tanθ) = tanθ secθ
Proof:
LHS
= (secθ – cosθ)(cotθ + tanθ)
= \(\large (\frac {1}{cosθ}\) – cosθ\(\large )\) \(\large (\frac {cosθ}{sinθ}\) + \(\large \frac {sinθ}{cosθ})\)
= \(\large (\frac {1\,–\,cos²θ}{cosθ})\) × \(\large (\frac {cos²θ\,+\,sin²θ}{sinθ\,·\,cosθ})\)
= \(\large \frac {sin²θ}{cosθ}\) × \(\large \frac {1}{sinθ\,·\,cosθ}\) …[∵ sin²θ + cos²θ = 1 , 1 – cos²θ = sin²θ]
= \(\large \frac {sinθ}{cosθ}\) × \(\large \frac {1}{cosθ}\)
= tanθ × secθ
= R.H.S.
Hence proved.
(5) cotθ + tanθ = cosecθ secθ
Proof:
LHS
= cotθ + tanθ
= \(\large \frac {cosθ}{sinθ}\) + \(\large \frac {sinθ}{cosθ}\)
= \(\large (\frac {cos²θ\,+\,sin²θ}{sinθ\,·\,cosθ})\)
= \(\large (\frac {1}{sinθ\,·\,cosθ})\) …[∵ sin²θ + cos²θ = 1]
= cosecθ × secθ
= RHS
Hence proved.
(6) \(\large \frac {1}{secθ\,–\,tanθ}\) = secθ + tanθ
Proof:
LHS
= \(\large \frac {1}{secθ\,–\,tanθ}\)
= \(\large \frac {1(secθ\,+\,tanθ)}{(secθ\,–\,tanθ)(secθ\,+\,tanθ)}\)
= \(\large \frac {secθ\,+\,tanθ}{sec²θ\,–\,tan²θ}\)
= \(\large \frac {secθ\,+\,tanθ}{1}\) …[∵ sec²θ = 1 + tan²θ , sec²θ – tan²θ = 1]
= secθ + tanθ
= RHS
Hence proved.
(7) sin⁴θ – cos⁴θ = 1 – 2cos²θ
Proof:
LHS
= sin⁴θ – cos⁴θ
= (sin²θ)² – (cos²θ)²
= (sin²θ + cos²θ) (sin²θ – cos²θ)
= 1 × (sin²θ – cos²θ) …[∵ sin²θ + cos²θ = 1]
= sin²θ – cos²θ
= 1 – cos²θ – cos²θ …[∵ sin²θ = 1 – cos²θ]
= 1 – 2 cos²θ
= R.H.S.
Hence proved.
(8) secθ + tanθ = \(\large \frac {cosθ}{1\,–\,sinθ}\)
Proof:
LHS
= secθ + tanθ
= \(\large \frac {1}{cosθ}\) + \(\large \frac {sinθ}{cosθ}\)
= \(\large \frac {1\,+\,sinθ}{cosθ}\)
= \(\large \frac {(1\,+\,sinθ)(1\,–\,sinθ)}{cosθ(1\,–\,sinθ)}\)
= \(\large \frac {1\,–\,sin²θ}{cosθ(1\,–\,sinθ)}\)
= \(\large \frac {cos²θ}{cosθ(1\,–\,sinθ)}\) …[∵ sin²θ + cos²θ = 1, sin²θ = 1 – cos²θ]
= \(\large \frac {cosθ}{1\,–\,sinθ}\)
= RHS
Hence proved.
(9) If tanθ + \(\large \frac {1}{tanθ}\) = 2, then show that tan²θ + \(\large \frac {1}{tan²θ}\) = 2
Proof:
tanθ + \(\large \frac {1}{tanθ}\) = 2
\(\large (\)tanθ + \(\large \frac {1}{tanθ})²\) = 4 …[Squaring both sides]
tan²θ + 2tanθ \(\large \frac {1}{tanθ}\) + \(\large \frac {1}{tan²θ}\) = 4
tan²θ + 2 + \(\large \frac {1}{tan²θ}\) = 4
tan²θ + \(\large \frac {1}{tan²θ}\) = 4 – 2
tan²θ + \(\large \frac {1}{tan²θ}\) = 2
Hence proved.
(10) \(\large \frac {tan\,A}{(1\,+\,tan²\,A)²}\) + \(\large \frac {cot\,A}{(1\,+\,cot²\,A)²}\) = sin A cos A
Proof:
LHS
= \(\large \frac {tan\,A}{(sec²\,A)²}\) + \(\large \frac {cot\,A}{(cosec²\,A)²}\)
= \(\large \frac {tan\,A}{sec⁴\,A}\) + \(\large \frac {cot\,A}{cosec⁴\,A}\)
= tan A . cos⁴A + cot A . sin⁴A
= \(\large \frac {sin\,A}{cos\,A}\) . cos⁴A + \(\large \frac {cos\,A}{sin\,A}\) . sin⁴A
= sin A . cos³A + cosA . sin³A
= sin A . cosA (cos²A + sin²A)
= sin A . cosA × 1 …[∵ sin²A + cos²A = 1]
= sin A . cos A
= R.H.S.
Hence proved.
(11) sec⁴A (1 – sin⁴A) – 2tan²A = 1
Proof:
LHS
= sec⁴A (1 – sin⁴A) – 2tan²A
= sec⁴A (1 + sin²A) (1 – sin²A) – 2tan²A
= sec⁴A × (1 + sin²A) × cos²A – 2tan²A …[∵ sin²θ + cos²θ = 1, 1 – sin²θ = cos²θ]
= \(\large \frac {1}{cos⁴A}\) (1 + sin²A) × cos²A – 2 \(\large \frac {sin²A}{cos²A}\)
= \(\large \frac {1\,+\,sin²A}{cos²A}\) – 2 \(\large \frac {sin²\,A}{cos²\,A}\)
= \(\large \frac {1\,+\,sin²A\,–\,2sin²A}{cos²A}\)
= \(\large \frac {1\,–\,sin²A}{cos²A}\)
= \(\large \frac {cos²A}{cos²A}\) …[∵ sin²θ + cos²θ = 1, 1 – sin²θ = cos²θ]
= 1
= RHS
Hence proved.
(12) \(\large \frac {tanθ}{secθ\,+\,1}\) = \(\large \frac {tanθ\,+\,secθ\,+\,1}{tanθ\,+\,secθ\,–\,1}\)
Proof:
1 + tan²θ = sec²θ
tan²θ = sec²θ – 1
tanθ × tanθ = (secθ + 1) (secθ – 1)
\(\large \frac {tanθ}{secθ\,+\,1}\) = \(\large \frac {secθ\,+\,1}{tanθ}\)
\(\large \frac {tanθ}{secθ\,+\,1}\) = \(\large \frac {tanθ\,+\,secθ\,+\,1}{tanθ\,+\,secθ\,–\,1}\) …[By Theorem on equal ratios]
Hence proved.
Practice set 6.2
1. A person is standing at a distance of 80m from a church looking at its top. The angle of elevation is 45°. Find the height of the church.
Solution:
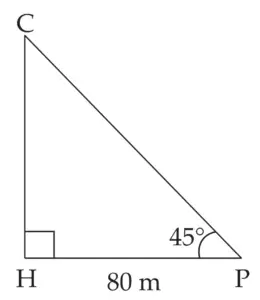
CH represents the height of the church and C represents its top. P is the position of the person at a distance of 80 m from the church.
∴ PH = 80 m
∠CPH is the angle of the elevation
∴ ∠CPH = 45°
In ∆PHC,
∠CHP = 90°
∴ tan ∠CPH = \(\large \frac {CH}{PH}\) …[By definition]
∴ tan 45° = \(\large \frac {CH}{80}\)
∴ 1 = \(\large \frac {CH}{80}\)
∴ CH = 80 m
Ans: Height of the church is 80 m.
2. From the top of a lighthouse, an observer looking at a ship makes an angle of depression of 60°. If the height of the lighthouse is 90 metre, then find how far the ship is from the lighthouse. (\(\sqrt{3}\) = 1.73)
Solution:
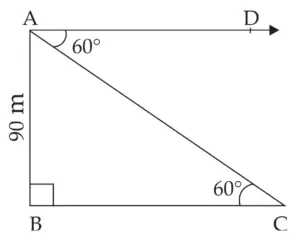
AB represents the height of the lighthouse.
AB = 90 m
C represents the position of ship.
∠DAC is the angle of depression
∴ DAC = 60°
∴ ∠DAC = ∠ACB = 60° …[Alternate angle theorem]
In ∆ABC,
∠ABC = 90°
∴ tan 60 = \(\large \frac {AB}{BC}\) …[By Definition]
∴ \(\sqrt{3}\) = \(\large \frac {90}{BC}\)
∴ BC = \(\large \frac {90}{\sqrt{3}}\)
∴ BC = \(\large \frac {90\,\sqrt{3}}{\sqrt{3}\,×\,\sqrt{3}}\)
∴ BC = \(\large \frac {90\,\sqrt{3}}{3}\)
∴ BC = 30 \(\sqrt{3}\)
∴ BC = 30 (1.73)
∴ BC = 51.9 m
Ans: The distance of the ship from the lighthouse is 51.90 m.
3. Two buildings are facing each other on a road of width 12 metre. From the top of the first building, which is 10 metre high, the angle of elevation of the top of the second is found to be 60°. What is the height of the second building?
Solution:
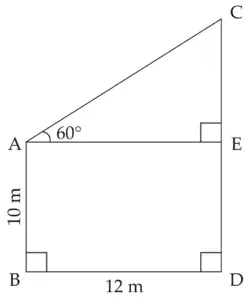
AB and CD represent the height of the two buildings, on either side of a road.
AB = 10 m, BD = 12 m
∠CAE is the angle of the elevation.
∴ ∠CAE = 60°
□ ABDE is a rectangle …[By definition]
AB = DE = 10 m …[Opposite sides of a rectangle]
AE = BD = 12 m
In ∆AEC,
∠AEC = 90°
∴ tan ∠CAE = \(\large \frac {CE}{AW}\) …[By definition]
∴ tan 60° = \(\large \frac {CE}{13}\)
∴ \(\sqrt{3}\) = \(\large \frac {CE}{13}\)
∴ CE = 12 × 3
∴ CE = 12 × 1.73
∴ CE = 20.76 m
CD = CE + DE …[C – E – D]
∴ CD = 20.76 + 10
∴ CD = 30.76 m
Ans: Height of the second building is 30.76 m.
4. Two poles of heights 18 metre and 7 metre are erected on a ground. The length of the wire fastened at their tops in 22 metre. Find the angle made by the wire with the horizontal.
Solution:
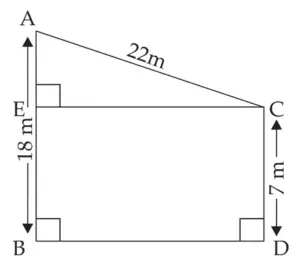
AB and CD represent the height of the two poles.
AC is the length of the wire of length 22 m joining top A and top C of two poles.
AC = 22 m
∠ACE is the angle made by the wire with the horizontal.
□ EBDC is a rectangle …[By Definition]
BE = CD = 7m …[Opposite sides of rectangle]
AB = AE + BE …[A – E – B]
∴ 18 = AE + 7
∴ 18 – 7 = AE
∴ AE = 11 m
In ∆AEC,
∠AEC = 90°
∴ sin ∠ACE = \(\large \frac {AE}{AC}\) …[By definition]
∴ sin ∠ACE = \(\large \frac {11}{22}\)
∴ sin ∠ACE = \(\large \frac {1}{2}\)
But, sin 30° = \(\large \frac {1}{2}\)
∴ sin ∠ACE = sin 30°
∴ ∠ACE = 30°
Ans: The angle made by the wire with the horizontal is 30°.
5. A storm broke a tree and the treetop rested 20 m from the base of the tree, making an angle of 60° with the horizontal. Find the height of the tree.
Solution:
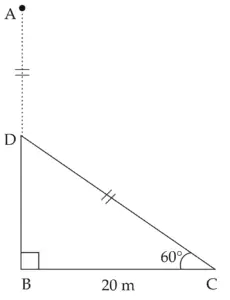
AB represents the height of the tree.
Tree breaks at D. AD represents the broken part of the tree which takes the position DC.
∴ AD = DC
∠DCB = 60°
∴ BC = 20 m
In ∆DBC,
∠DBC = 90°
∴ tan 60° = \(\large \frac {DB}{BC}\) …[By Definition]
∴ \(\sqrt{3}\) = \(\large \frac {DB}{20}\)
∴ DB = \(\large \frac {20}{\sqrt{3}}\)
∴ DB = 20(1.73)
∴ DB = 34.60 m
cos 60° = \(\large \frac {DB}{BC}\) …[By Definition]
∴ \(\large \frac {1}{2}\) = \(\large \frac {20}{DC}\)
∴ DC = 20 × 2
∴ DC = 40 m
∴ AD = DC = 40 m
∴ AB = AD + DB …[A – D – B]
∴ AB = 40 + 34.60
∴ AB = 74.60 m
Ans: The height of the tree is 74.60 m.
6. A kite is flying at a height of 60 m above the ground. The string attached to the kite is tied at the ground. It makes an angle of 60° with the ground. Assuming that the string is straight, find the length of the string. (\(\sqrt{3}\) = 1.73)
Solution:
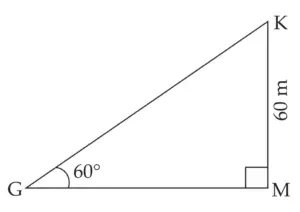
‘K’ is the position of the kite in the sky, 60 m above the ground level, KG represents the length of the string.
∠KGM is the angle between string and the ground ∠KGM = 60°
In ∆KMG,
∠KMG = 90°
∴ sin ∠KGM = \(\large \frac {KM}{GK}\) …[By Definition]
∴ sin 60° = \(\large \frac {60}{GK}\)
∴ \(\large \frac {\sqrt{3}}{2}\) = \(\large \frac {60}{GK}\)
∴ GK = \(\large \frac {60\,×\,2}{\sqrt{3}}\)
∴ GK = \(\large \frac {120}{\sqrt{3}}\)
∴ GK = \(\large \frac {120\,×\,\sqrt{3}}{\sqrt{3}\,×\,\sqrt{3}}\)
∴ GK = \(\large \frac {120\sqrt{3}}{3}\)
∴ GK = 40 \(\sqrt{3}\)
∴ GK = 40 × 1.73
∴ GK = 69.20 m
Ans: Length of the string is 69.20 m.
Problem Set 6
1. Choose the correct alternative answer for the following questions.
(1) sinθ cosecθ = ?
(A) 1
(B) 0
(C) \(\large \frac {1}{2}\)
(D) \(\sqrt{2}\)
Ans: Option (A) : 1
(2) cosec 45° =?
(A) \(\large \frac {1}{\sqrt{2}}\)
(B) \(\sqrt{2}\)
(C) \(\large \frac {\sqrt{3}}{2}\)
(D) \(\large \frac {2}{\sqrt{3}}\)
Ans: Option (B) : \(\sqrt{2}\)
(3) 1 + tan²θ = ?
(A) cot²θ
(B) cosec²θ
(C) sec²θ
(D) tan²θ
Ans: Option (C) : sec²θ
(4) When we see at a higher level, from the horizontal line, the angle formed is _____.
(A) angle of elevation.
(B) angle of depression.
(C) 0
(D) straight angle.
Ans: Option (A) : angle of elevation.
2. If sinθ = \(\large \frac {11}{61}\), find the values of cosθ using trigonometric identity.
Solution:
sinθ = \(\large \frac {11}{61}\)
We know that,
sin²θ + cos²θ = 1
∴ \(\large (\frac {11}{61})²\) + cos²θ = 1
∴ \(\large \frac {121}{3721}\) + cos²θ = 1
∴ cos²θ = 1 – \(\large \frac {121}{3721}\)
∴ cos²θ = \(\large \frac {3721\,–\,121}{3721}\)
∴ cos²θ = \(\large \frac {3600}{3721}\)
∴ cosθ = \(\large \frac {60}{61}\) …[Taking square roots]
Ans: cosθ = \(\large \frac {60}{61}\)
3. If tanθ = 2, find the values of other trigonometric ratios.
Solution:
tanθ = 2
We know that,
1 + tan²θ = sec²θ
∴ 1 + 2² = sec²θ
∴ sec²θ = 1 + 4
∴ sec²θ = 5
∴ secθ = \(\sqrt{5}\) …[Taking square roots]
cosθ = \(\large \frac {1}{secθ}\)
∴ cosθ = \(\large \frac {1}{\sqrt{5}}\)
tanθ = \(\large \frac {sinθ}{cosθ}\)
∴ sinθ = tanθ × cosθ
∴ sinθ = 2 × \(\large \frac {1}{\sqrt{5}}\)
∴ sinθ = \(\large \frac {2}{\sqrt{5}}\)
cosecθ =\(\large \frac {1}{sinθ}\)
∴ cosecθ =\(\large \frac {1}{\frac {2}{\sqrt{5}}\)
∴ cosecθ =\(\large \frac {\sqrt{5}}{2}\)
cotθ =\(\large \frac {1}{tanθ}\)
∴ cotθ =\(\large \frac {1}{2}\)
Ans: secθ = \(\sqrt{5}\), cosθ = \(\large \frac {1}{\sqrt{5}}\), sinθ = \(\large \frac {2}{\sqrt{5}}\), cosecθ =\(\large \frac {\sqrt{5}}{2}\) and cotθ =\(\large \frac {1}{2}\).
4. If secθ = \(\large \frac {13}{12}\), find the values of other trigonometric ratios.
Solution:
secθ = \(\large \frac {13}{12}\)
∴ cosθ = \(\large \frac {1}{secθ}\)
∴ cosθ = \(\large \frac {1}{\frac {13}{12}}\)
∴ cosθ = \(\large \frac {12}{13}\)
sin²θ + cos²θ = 1
∴ sin²θ + \(\large (\frac {12}{13})²\) = 1
∴ sin²θ = 1 – \(\large \frac {144}{169}\)
∴ sin²θ = \(\large \frac {169\,–\,144}{169}\)
∴ sin²θ = \(\large \frac {25}{169}\)
∴ sinθ = \(\large \frac {5}{13}\) …[Taking square roots]
cosecθ = \(\large \frac {1}{sinθ}\)
∴ cosecθ = \(\large \frac {1}{\frac {5}{13}}\)
∴ cosecθ = \(\large \frac {13}{5}\)
tanθ = \(\large \frac {sinθ}{cosθ}\)
∴ tanθ = \(\large \frac {\frac {5}{13}}{\frac {12}{13}}\)
∴ tanθ = \(\large \frac {5}{13}\) × \(\large \frac {12}{13}\)
∴ tanθ = \(\large \frac {5}{12}\)
cotθ = \(\large \frac {1}{tanθ}\)
∴ cotθ = \(\large \frac {1}{\frac {5}{12}}\)
∴ cotθ = \(\large \frac {12}{5}\)
Ans: cosθ = \(\large \frac {12}{13}\), sinθ = \(\large \frac {5}{13}\), cosecθ = \(\large \frac {13}{5}\), tanθ = \(\large \frac {5}{12}\) and cotθ = \(\large \frac {12}{5}\).
5. Prove the following.
(1) secθ (1 – sinθ) (secθ + tanθ) = 1
Proof:
LHS
= secθ (1 – sinθ) (secθ + tanθ)
= \(\large \frac {1}{cosθ}\) (1 – sinθ) \(\large( \frac {1}{cosθ}\) + \(\large \frac {sinθ}{cosθ})\)
= \(\large \frac {(1\,–\,sinθ)}{cosθ}\) · \(\large \frac {(1\,+\,sinθ)}{cosθ}\)
= \(\large \frac {1\,–\,sin²θ}{cos²θ}\)
= \(\large \frac {cos²θ}{cos²θ}\) …[∵ sin²θ + cos²θ = 1 , 1 – cos²θ = sin²θ]
= 1
= RHS
Hence proved.
(2) (secθ + tanθ) (1 – sinθ) = cosθ
Proof:
LHS
= (secθ + tanθ) (1 – sinθ)
= \(\large( \frac {1}{cosθ}\) + \(\large \frac {sinθ}{cosθ})\) (1 – sinθ)
= \(\large \frac {(1\,+\,sinθ)}{cosθ}\) (1 – sinθ)
= \(\large \frac {1\,–\,sin²θ}{cosθ}\)
= \(\large \frac {cos²θ}{cosθ}\) …[∵ sin²θ + cos²θ = 1 , 1 – cos²θ = sin²θ]
= cosθ
= RHS
Hence proved.
(3) sec²θ + cosec²θ = sec²θ × cosec²θ
Proof:
LHS
= sec²θ + cosec²θ
= \(\large \frac {1}{cos²θ}\) + \(\large \frac {1}{sin²θ}\)
= \(\large \frac {sin²θ\,+\,cos²θ}{cos²θ\,×\,sin²θ}\)
= \(\large \frac {1}{cos²θ\,×\,sin²θ}\)
= \(\large \frac {1}{cos²θ}\) × \(\large \frac {1}{sin²θ}\)
= sec²θ × cosec²θ
= RHS
Hence proved.
(4) cot²θ – tan²θ = cosec²θ – sec²θ
Proof:
LHS
= cot²θ – tan²θ
= (cosec²θ – 1) – (sec²θ – 1) …[∵ 1 + cot²θ = cosec²θ , cot²θ = cosec²θ – 1 and sec²θ = 1 + tan²θ , tan²θ = sec²θ – 1]
= cosec²θ – 1 – sec²θ + 1
= cosec²θ – sec²θ
= R.H.S.
Hence proved.
(5) tan⁴θ + tan²θ = sec⁴q – sec²θ
Proof:
LHS
= tan⁴q + tan²θ
= tan²θ (tan²θ + 1)
= (sec²θ – 1) (sec²θ) …[∵ 1 + tan²θ = sec²θ , tan²θ = sec²θ – 1]
= sec⁴θ – sec²θ
= R.H.S.
Hence proved.
(6) \(\large \frac {1}{1\,–\,sinθ}\) + \(\large \frac {1}{1\,+\,sinθ}\) = 2 sec²θ
Proof:
LHS
= \(\large \frac {1}{1\,–\,sinθ}\) + \(\large \frac {1}{1\,+\,sinθ}\)
= \(\large \frac {1\,+\,sinθ\,+\,1\,–\,sinθ}{(1\,–\,sinθ)(1\,+\,sinθ)}\)
= \(\large \frac {2}{1\,–\,sin²θ}\)
= \(\large \frac {2}{cos²θ}\) …[∵ sin²θ + cos²θ = 1 , 1 – cos²θ = sin²θ]
= 2 sec²θ
= RHS
Hence proved.
(7) sec⁶x – tan⁶x = 1 + 3sec²x × tan²x
Proof:
LHS
= sec⁶x – tan⁶x
= (sec²x)³ – (tan²x)³
= (sec²x – tan²x)³ + 3sec²x tan²x (sec²x – tan²x)
= (1)³ + 3sec²x . tan²x (1) …[∵ sec²θ = 1 + tan²θ , tan²θ = sec²θ – 1]
= 1 + 3sec²x . tan²x
= R.H.S.
Hence proved.
(8) \(\large \frac {tanθ}{secθ\,+\,1}\) = \(\large \frac {secθ\,–\,1}{tanθ}\)
Proof:
LHS
= \(\large \frac {tanθ}{secθ\,+\,1}\)
= \(\large \frac {tanθ}{secθ\,+\,1}\) \(\large \frac {secθ\,–\,1}{secθ\,–\,1}\)
= \(\large \frac {tanθ(secθ\,–\,1)}{(secθ\,+\,1)(secθ\,–\,1)}\)
= \(\large \frac {tanθ(secθ\,–\,1)}{sec²θ\,–\,1}\)
= \(\large \frac {tanθ(secθ\,–\,1)}{tan²θ}\)
= \(\large \frac {secθ\,–\,1}{tanθ}\)
= RHS
Hence proved.
(9) \(\large \frac {tan³θ\,–\,1}{tanθ\,–\,1}\) = sec²θ + tanθ
Proof:
LHS
= \(\large \frac {tan³θ,–\,1}{tanθ\,–\,1}\)
= \(\large \frac {tan³θ\,–\,1³}{tanθ\,–\,1}\)
= \(\large \frac {(tanθ\,–\,1)(tan²θ\,+\,tanθ\,+\,1)}{tanθ\,–\,1}\)
= tan²θ + 1 + tanθ
= sec²θ + tanθ
= R.H.S.
Hence proved.
(10) \(\large \frac {sinθ\,–\,cosθ\,+\,1}{sinθ\,+\,cosθ\,–\,1}\) = \(\large \frac {1}{secθ\,–\,tanθ}\)
Proof:
LHS
= \(\large \frac {1}{secθ\,–\,tanθ}\)
= \(\large \frac {1}{\large\frac {1}{cosθ} \,–\,\large\frac {sinθ}{cosθ}}\)
= \(\large \frac {1}{\large\frac {1\,–\,sinθ}{cosθ}}\)
= \(\large \frac {cosθ}{1\,–\,sinθ}\) …(i)
Now, we know that,
sin²θ + cos²θ = 1
∴ cos²θ = 1 – sin²θ
∴ cosθ × cosθ = (1 – sinθ) (1 + sinθ)
∴ \(\large \frac {cosθ}{1\,–\,sinθ}\) = \(\large \frac {1\,+\,sinθ}{cosθ}\)
∴ \(\large \frac {cosθ}{1\,–\,sinθ}\) = \(\large \frac {1\,+\,sinθ\,–\,cosθ}{cosθ\,–\,(1\,–\,sinθ)}\) …[By theorem on equal ratios]
∴ \(\large \frac {cosθ}{1\,–\,sinθ}\) = \(\large \frac {1\,+\,sinθ\,–\,cosθ}{cosθ\,–\,1\,+\,sinθ}\) …(ii)
From (i) and (ii),
\(\large \frac {sinθ\,–\,cosθ\,+\,1}{sinθ\,+\,cosθ\,–\,1}\) = \(\large \frac {1}{secθ\,–\,tanθ}\)
Hence proved.
6. A boy standing at a distance of 48 meters from a building observes the top of the building and makes an angle of elevation of 30°. Find the height of the building.
Solution:
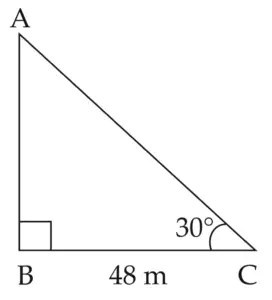
AB represents the height of the building. C represents the position of the boy at a distance of 48 m from the building.
∠ ACB is the angle of elevation
∴ ∠ACB = 30°
In ∆ABC,
∠ABC = 90°
∴ tan ∠ACB = \(\large \frac {AB}{BC}\) …[By Definition]
∴ tan 30 = \(\large \frac {AB}{48}\)
∴ \(\large \frac {1}{\sqrt{3}}\) = \(\large \frac {AB}{48}\)
∴ AB = \(\large \frac {48}{\sqrt{3}}\)
∴ AB = \(\large \frac {48\,×\,\sqrt{3}}{\sqrt{3}\,×\,\sqrt{3}}\)
∴ AB = \(\large \frac {48\sqrt{3}}{3}\)
∴ AB = 16 × \(\sqrt{2}\)
∴ AB = 16 × 1.73
∴ AB = 27.68 m
Ans: The height of the building is 27.68 m.
7. From the top of the light-house, an observer looks at a ship and finds the angle of depression to be 30°.If the height of the light-house is 100 meters, then find how far the ship is from the light-house.
Solution:
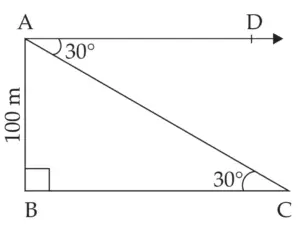
AB represents the height of the lighthouse.
∴ AB = 100 m
C represents the position of the ship.
∠DAC is the angle of depression.
∴ ∠DAC = ∠ACB = 30° …[Alternate angle theorem]
In ∆ABC,
∠ABC = 90°
∴ tan ∠ACB = \(\large \frac {AB}{BC}\) …[By Definition]
∴ tan 30° = \(\large \frac {100}{BC}\)
∴ \(\large \frac {1}{\sqrt{3}}\) = \(\large \frac {100}{BC}\)
∴ BC = 100 \(\sqrt{3}\)
∴ BC = 100 × 1.73
∴ BC = 173 m
Ans: The distance of the ship from the lighthouse is 173 m.
8. Two buildings are in front of each other on a road of width 15 meters. From the top of the first building, having a height of 12 meter, the angle of elevation of the top of the second building is 30°.What is the height of the second building?
Solution:
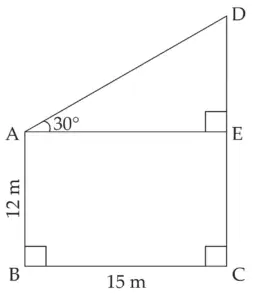
AB and CD represents the height of two
buildings at distance of 15 m, i.e. BC = 15 m, AB = 12 m
∠DAE is the angle of elevation.
∠DAE = 30°
□ ABCE is a rectangle …[By Definition]
AB = EC = 12 m
BC = AE = 15 m …[Opposite sides of rectangle]
In ∆AED,
∠AED = 90°
∴ tan ∠DAE = \(\large \frac {DE}{AE}\) …[By Definition]
∴ tan 30° = \(\large \frac {DE}{15}\)
∴ \(\large \frac {1}{\sqrt{3}}\) = \(\large \frac {DE}{15}\)
∴ DE = \(\large \frac {15}{\sqrt{3}}\)
∴ DE = \(\large \frac {15\,×\,\sqrt{3}}{\sqrt{3}\,×\,\sqrt{3}}\)
∴ DE = \(\large \frac {15\,×\,\sqrt{3}}{3}\)
∴ DE = 5\(\sqrt{3}\)
∴ DE = 5 × 1.73
∴ DE = 8.65 m
CD = CE + DE …[C – E – D]
∴ CD = 12 + 8.65
∴ CD = 20.65 m
Ans: Height of the second building is 20.65 m
9. A ladder on the platform of a fire brigade van can be elevated at an angle of 70° to the maximum. The length of the ladder can be extended upto 20m. If the platform is 2m above the ground, find the maximum height from the ground upto which the ladder can reach. (sin 70° = 0.94)
Solution:
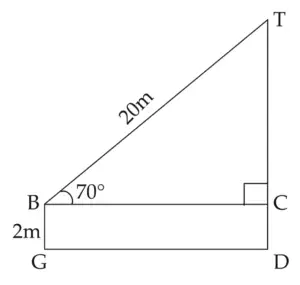
GD is ground level. BC is base of the ladder of the fire brigade van at a height of 2 m from ground level.
‘T’ is top of ladder of the fire brigade van at the maximum height
∴ ∠TBC = 70° …[Angle of elevation]
BT is the length of the ladder
BT = 20 m, BG = 2 m
□ BGDC is a rectangle …[By Definition]
∴ BG = CD = 2m …[Opposite sides of a rectangle]
In ∆BCT,
∠BCT = 90°
∴ sin ∠TBC = \(\large \frac {TC}{TB}\) …[By Definition]
∴ sin 70° = \(\large \frac {TC}{20}\)
∴ 0.94 = \(\large \frac {TC}{20}\)
∴ TC = 0.94 × 20
∴ TC = 18.80 m
TD = TC + CD …[T – C – D]
∴ TD = 18.80 + 2
∴ TD = 20.80 m
Ans: Other end of the ladder can reach 20.80 m above the ground ladder.
10. While landing at an airport, a pilot made an angle of depression of 20°. Average speed of the plane was 200 km/hr. The plane reached the ground after 54 seconds. Find the height at which the plane was when it started landing. (sin 20° = 0.342)
Solution:
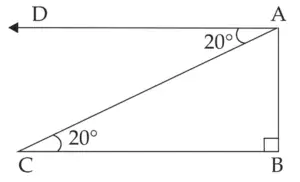
A represents the position of the plane above the ground.
‘C’ is the landing point of the plane on the ground.
AB represents the height of the plane from the ground.
∠DAC is the angle of depression
∠DAC = ∠ACB = 20°
Distance (AC) = speed × time
∴ Distance (AC) = 200 km/hr × 54 sec
∴ Distance (AC) = 200 km/hr × \(\large \frac {54}{3600}\) …[∵ 1 hr = 3600 sec]
∴ Distance (AC) = 3 km
∴ AC = 3000 m
In ∆ABC,
∠ABC = 90°
∴ sin ∠ACB = \(\large \frac {AB}{AC}\) …[By Definition]
∴ sin 20° = \(\large \frac {AB}{3000}\)
∴ 0.342 = \(\large \frac {AB}{3000}\)
∴ AB = 0.342 × 3000
∴ AB = 1026 km.
Ans: Plane was at a height of 1026 km, when it started landing.
