Chapter 8 – Quadrilateral : Constructions and Types
Practice set 8.1
1. Construct the following quadrilaterals of given measures.
(1) In □ MORE, l(MO) = 5.8 cm, l(OR) = 4.4 cm, m∠ M = 58°, m∠ O = 105°, m∠ R = 90°.
Ans:
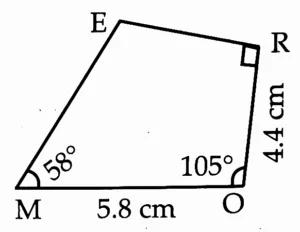
Rough Figure
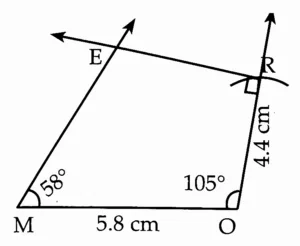
This is the required construction.
(2) Construct □ DEFG such that l(DE) = 4.5 cm, l(EF) = 6.5 cm, l(DG) = 5.5 cm, l(DF) = 7.2 cm, l(EG) = 7.8 cm.
Ans:
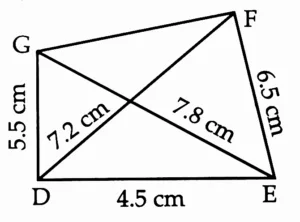
Rough Figure
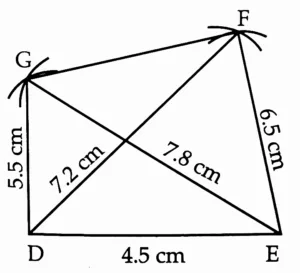
This is the required construction.
(3) In □ ABCD, l(AB) = 6.4 cm, l(BC) = 4.8 cm, m∠ A = 70°, m∠ B = 50°, m∠ C = 140°.
Ans:
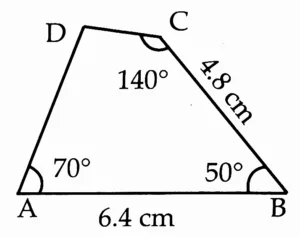
Rough Figure
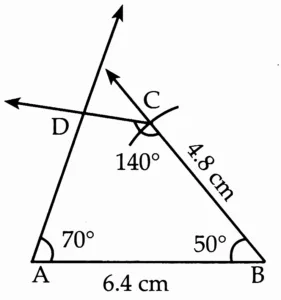
This is the required construction.
(4) Construct □ LMNO such that l(LM) = l(LO) = 6 cm, l(ON) = l(NM) = 4.5 cm, l(OM) = 7.5 cm.
Ans:
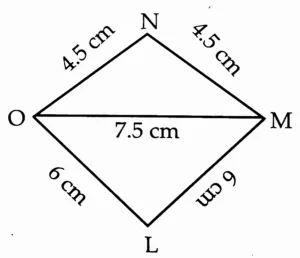
Rough Figure
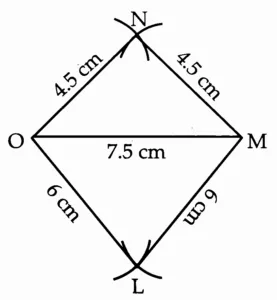
This is the required construction.
Practice set 8.2
1. Draw a rectangle ABCD such that l(AB) = 6.0 cm and l(BC) = 4.5 cm.
Ans:
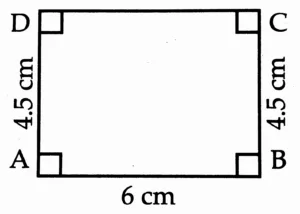
Rough Figure
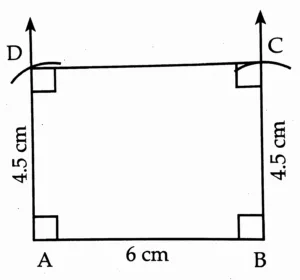
This is the required construction.
2. Draw a square WXYZ with side 5.2 cm.
Ans:
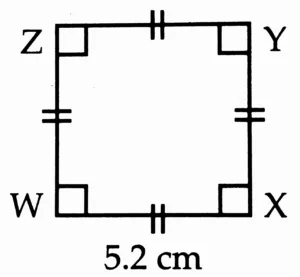
Rough Figure
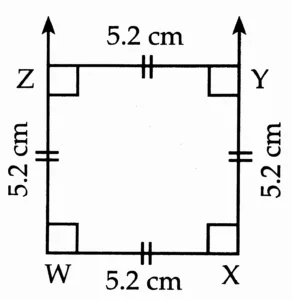
This is the required construction.
3. Draw a rhombus KLMN such that its side is 4 cm and m∠ K = 75°.
Ans:
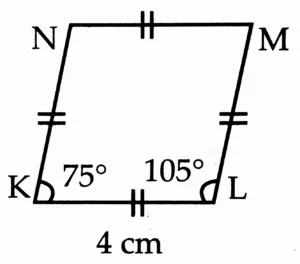
Rough Figure
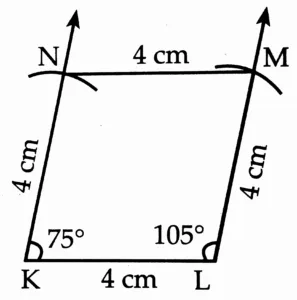
This is the required construction.
4. If diagonal of a rectangle is 26 cm and one side is 24 cm, find the other side.
Solution:
Let □ ABCD be the rectangle.
l(BC) = 24cm
l(AC) = 26cm
In ∆ABC,
m∠ABC = 90° …[Angle of a rectangle]
∴ By Pythagoras theorem,
∴ [l(AC)]² = [l(AB)]2 + [l(BC)]²
∴ (26)² = [l(AB)]² + (24)²
∴(26)² – (24)² = [l(AB)]²
∴[l(AB)]² = 676 – 576
∴ [l(AB)]² = 100
∴ \(\sqrt{[l(AB)]²}\) = \(\sqrt{100}\) …[Taking square root on both sides]
∴ l(AB) = 10 cm
Ans: The length of the other side is 10 cm.
4. If diagonal of a rectangle is 26 cm and one side is 24 cm, find the other side.
Solution:
Let □ ABCD be the rectangle.
l(BC) = 24cm
l(AC) = 26cm
In ∆ABC,
m∠ABC = 90° …[Angle of a rectangle]
∴ By Pythagoras theorem
∴ [l(AC)]² = [l(AB)]2 + [l(BC)]²
∴ (26)² = [l(AB)]² + (24)²
∴(26)² – (24)² = [l(AB)]²
∴[l(AB)]² = 676 – 576
∴ [l(AB)]² = 100
∴ \(\sqrt{[l(AB)]²}\) = \(\sqrt{100}\) …[Taking square root on both sides]
∴ l(AB) = 10 cm
Ans: The length of the other side is 10 cm.
5. Lengths of diagonals of a rhombus ABCD are 16 cm and 12 cm. Find the side and perimeter of the rhombus.
Solution:
In rhombus ABCD,
l(AC) = 16 cm
l(BD) = 12 cm.
Let the diagonals of rhombus ABCD intersect at point O.
l(AO) = \(\large \frac {1}{2}\) l(AC) …[Diagonals of a rhombus bisect each other]
∴ l(AO) = \(\large \frac {1}{2}\) × 16
∴ l(AO) = 8 cm
Also, l(DO) = \(\large \frac {1}{2}\) l(BD) …[Diagonals of a rhombus bisect each other]
∴ l(DO) = \(\large \frac {1}{2}\) × 12
∴ l(DO) = 6 cm
In ∆DOA,
m∠DOA = 90° ..[Diagonals of a rhombus are perpendicular to each other]
∴ By Pythagoras Theorem,
[l(AD)]² = [l(AO)]² + [l(DO)]²
[l(AD)]² = (8)² + (6)²
[l(AD)]² = 64 + 36
∴ [l(AD)]² = 100
∴ \(\sqrt{[l(AD)]²}\) = \(\sqrt{100}\) … [Taking square root on both sides]
∴ l(AD) = 10 cm
∴ l(AB) = l(BC) = l(CD) = l(AD) = 10 cm …[Sides of a rhombus are congruent]
Perimeter of rhombus ABCD
= l(AB) + l(BC) + l(CD) + l(AD)
= 10 + 10 + 10 + 10
= 40 cm
Ans: The side and perimeter of the rhombus are 10 cm and 40 cm respectively.
6. Find the length of diagonal of a square with side 8 cm
Solution:
Let □ XYWZ is the square of side 8cm.
Seg XW is a diagonal.
In ∆XYW,
m∠XYW = 90° … [Angle of a square]
∴ By Pythagoras Theorem,
[l(XW)]² = [l(XY)]² + [l(YW)]²
∴ [l(XW)]² = (8)² + (8)²
∴ [l(XW)]² = 64 + 64
∴ [l(XW)]² = 128
∴ \(\sqrt{[l(XW)]²}\) = \(\sqrt{128}\) …[Taking square root of both sides]
∴ l(XW) = \(\sqrt{64}\) × 2
∴ l(XW) = 8 \(\sqrt{2}\) cm
Ans: The length of the diagonal of the square is 8 \(\sqrt{2}\) cm.
7. Measure of one angle of a rhombus is 50°, find the measures of remaining three angles.
Solution:
Let □ ABCD be the rhombus.
m∠A = 50°
m∠C ≅ m∠A ….[Opposite angles of a rhombus are congruent]
∴ m∠C = 50°
Also, m∠D = m∠B …(i) ….[Opposite angles of a rhombus are congruent]
In □ ABCD,
m∠A + m∠B + m∠C + m∠D = 360° …[Sum of the measures of the angles of a quadrilateral is 360°]
∴ 50° + m∠B + 50° + m∠D = 360°
∴ m∠B + m∠D + 100° = 360°
∴ m∠B + m∠D = 360° – 100°
∴ m∠B + m∠B = 260° …[From (i)]
∴ 2m∠B = 260°
∴ m∠B = \(\large \frac {260}{2}\)
∴ m∠B = 130°
∴ m∠D ≅ m∠B = 130°
Ans: The measures of the remaining angles of the rhombus are 130°, 50° and 130°.
Practice set 8.3
1. Measures of opposite angles of a parallelogram are (3x – 2)° and (50 – x)°. Find the measure of its each angle.
Solution:
Let □ PQRS be the parallelogram.
m∠Q = (3x – 2)°
m∠S = (50 – x)°
m∠Q ≅ m∠S …(i) [Opposite angles of a parallelogram are congruent]
∴ 3x – 2 = 50 – x
∴ 3x + x = 50 + 2
∴ 4x = 52
∴ x = \(\large \frac {52}{5}\)
∴ x = 13
Now,
m∠Q = (3x – 2)°
∴ m∠Q = (3 × 13 – 2)°
∴ m∠Q = (39 – 2)°
∴ m∠Q = 37°
∴ m∠S ≅ m∠Q = 37° …[From(i)]
m∠P + m∠Q = 180°…[Adjacent angles of a parallelogram are supplementary]
∴ m∠P + 37° = 180°
∴ m∠P = 180° – 37°
∴ m∠P = 143°
∴ m∠R ≅ m∠P = 143° …[Opposite angles of a parallelogram are congruent]
Ans: The measures of the angles of the parallelogram are 37°, 143°, 37° and 143°.
2. Referring the adjacent figure of a parallelogram, write the answers of questions given below.
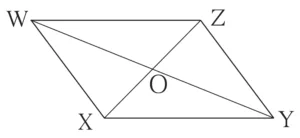
(1) If l(WZ) = 4.5 cm then l(XY) = ?
(2) If l(YZ) = 8.2 cm then l(XW) = ?
(3) If l(OX) = 2.5 cm then l(OZ) = ?
(4) If l(WO) = 3.3 cm then l(WY) = ?
(5) If m∠WZY = 120° then m∠WXY = ? and m∠ XWZ = ?
Solution:
(i) l(WZ) = 4.5 cm …[Given]
l(XY) = l(WZ) …[Opposite sides of a parallelogram are congruent ]
∴ l(XY) = 4.5 cm
(ii) l(YZ) = 8.2 cm …[Given]
l(XW) = l(YZ) …[Opposite sides of a parallelogram are congruent]
∴ l(XW) = 8.2 cm …[Given]
(iii) l(OX) = 2.5 cm …[Given]
l(OZ) = l(OX) …[Diagonals of a parallelogram bisect each other]
∴ l(OZ) = 2.5 cm
(iv) l(WO) = 3.3 cm …[Given]
l(WO) = \(\large \frac {1}{2}\) l(WY) …[Diagonals of a parallelogram bisect each other]
∴ 3.3 = \(\large \frac {1}{2}\) l(WY)
∴ 3.3 × 2 = l(WY)
∴ l(WY) = 6.6 cm
(v) m∠WZY =120° …[Given]
m∠WXY = m∠WZY …[Opposite angles of a parallelogram are congruent]
∴ m∠WXY = 120° …(i)
m∠XWZ + m∠WXY = 180° …[Adjacent angles of a parallelogram are supplementary]
∴ m∠XWZ + 120° = 180° …[From (i)]
∴ m∠XWZ = 180°– 120°
∴ m∠XWZ = 60°
3. Construct a parallelogram ABCD such that l(BC) = 7 cm, m∠ABC = 40°, l(AB) = 3 cm.
Solution:
Opposite sides of a parallelogram are congruent.
∴ l(AB) ≅ l(CD) = 3 cm
l(BC) ≅ l(AD) = 7 cm
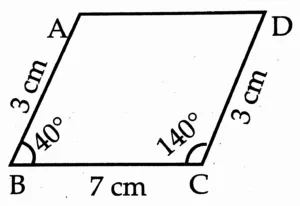
Rough Figure
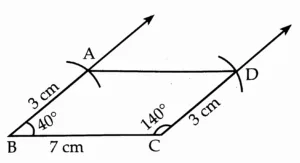
This is the required construction.
4. Ratio of consecutive angles of a quadrilateral is 1 : 2 : 3 : 4. Find the measure of its each angle. Write, with reason, what type of a quadrilateral it is.
Solution:
Let □ PQRS be the quadrilateral.
Ratio of consecutive angles of a quadrilateral is 1 : 2 : 3 : 4.
Let the common multiple be x.
∴ m∠P = x°
m∠Q = 2x°
m∠R = 3x°
m∠S = 4x°
In □ PQRS,
m∠P + m∠Q + m∠R + m∠S = 360° …[Sum of the measures of the angles of a quadrilateral is 360°]
∴x + 2x + 3x + 4x = 360
∴10x = 360
∴ x = \(\large \frac {360}{10}\)
∴ x = 36
∴ m∠P = x = 36
m∠Q = 2x = 2 × 36 = 72
m∠R = 3x = 3 × 36 = 108
m∠S = 4x = 4 × 36 = 144
∴ The measures of the angles of the quadrilateral are 36°, 72°, 108°, 144°.
Now,
m∠P + m∠S = 36° + 144° = 180°
Since interior angles are supplementary,
∴ Side PQ || side SR
m∠P + m∠Q = 36° + 72°
m∠P + m∠Q = 108° ≠ 180°
∴ Side PS is not parallel to side QR.
Since, one pair of opposite sides of the given quadrilateral is parallel.
∴ The given quadrilateral is a trapezium.
5. Construct □ BARC such that l(BA) = l(BC) = 4.2 cm, l(AC) = 6.0 cm, l(AR) = l(CR) = 5.6 cm
Ans:
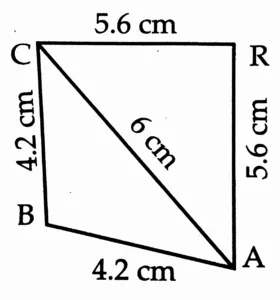
Rough Figure
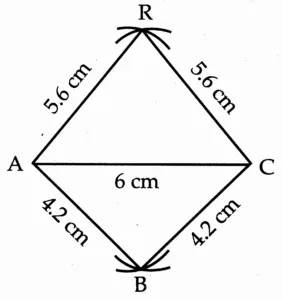
This is the required construction.
6. Construct □ PQRS, such that l(PQ) = 3.5 cm, l(QR) = 5.6 cm, l(RS) = 3.5 cm, m∠ Q = 110°, m∠ R = 70°. If it is given that □ PQRS is a parallelogram, which of the given information is unnecessary?
Solution:
The opposite sides of a parallelogram are congruent.
∴ Either l(PQ) or l(SR) is required.
To construct a parallelogram, lengths of adjacent sides and measure of one angle is required.
∴ Either l(PQ) and m∠Q or l(SR) and m∠R is the unnecessary information given in the question.
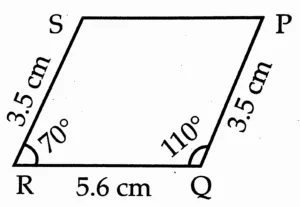
Rough Figure
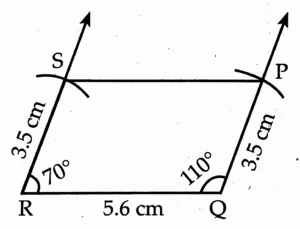
This is the required construction.
