Chapter 4 – Constructions of Triangles
Practice set 4.1
1. Construct ∆PQR, in which QR = 4.2 cm, m∠Q = 40° and PQ + PR = 8.5 cm
Explanation:
Line l is perpendicular bisector of seg DR
∴ PD = PR …(i) …[Perpendicular bisector theorem]
QD = 8.5 cm …(ii)
PQ + PD = QD …[Q – P – D]
∴ PQ + PR = 8.5 cm …[From (i) and (ii)]
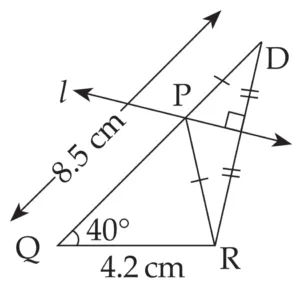
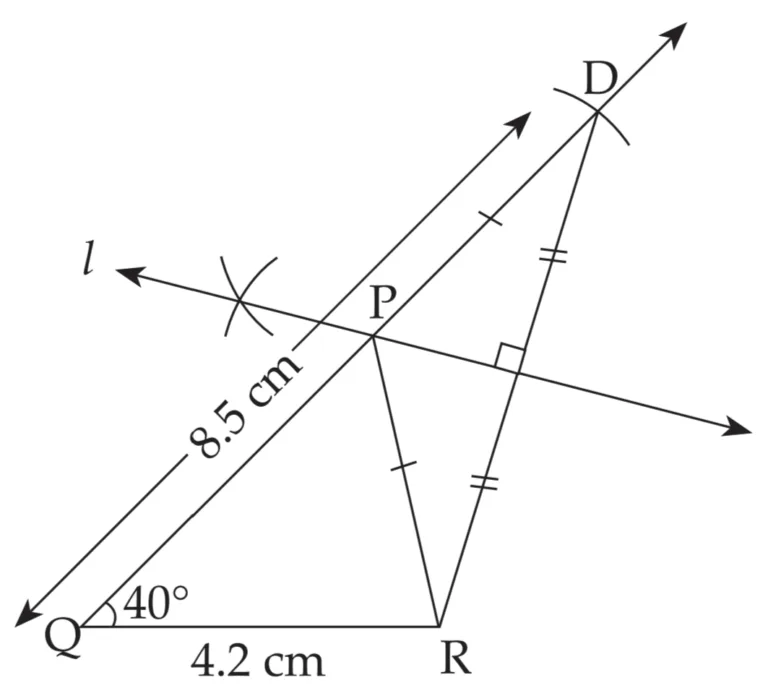
This is the required construction.
2. Construct ∆XYZ, in which YZ = 6 cm, XY + XZ = 9 cm. ∠XYZ = 50°.
Explanation:
Line l is perpendicular bisector of seg AZ
∴ XA = XZ …(i) [Perpendicular bisector theorem]
AY = 9 cm …(ii)
XY + XA = AY …[A – X – Y]
∴ XY + XZ = 9 cm …[From (i) and (ii)]
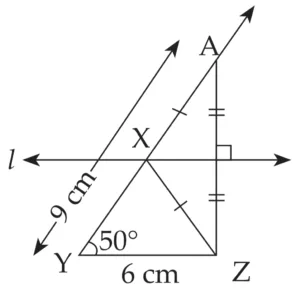
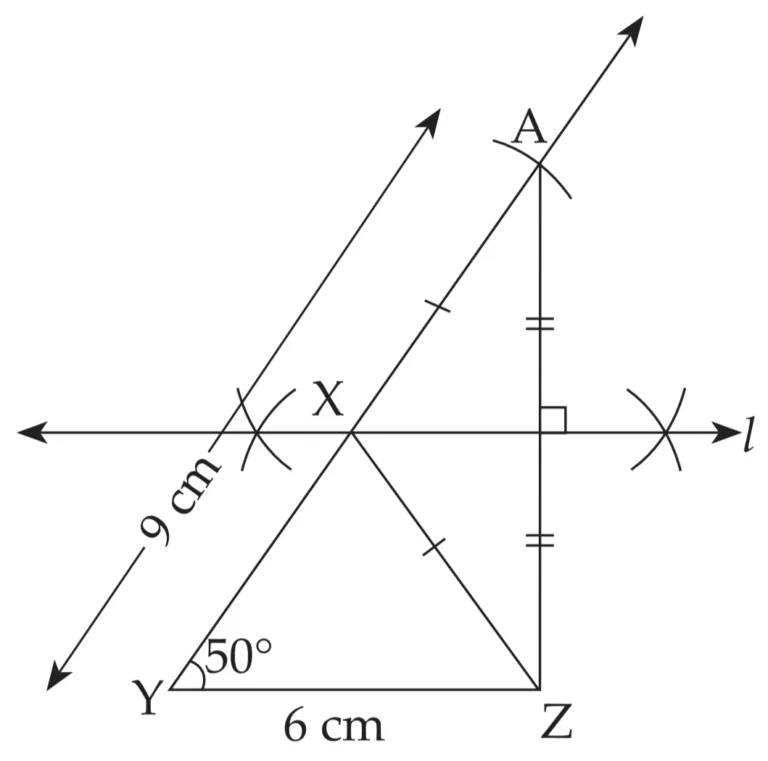
This is the required construction.
3. Construct ∆ABC, in which BC = 6.2 cm, ∠ACB = 50°, AB + AC = 9.8 cm.
Explanation:
Line l is perpendicular bisector of seg PB
∴ AP = AB …(i) [Perpendicular bisector theorem]
PC = 9.8 cm …(ii)
AC + AP = PC …[P – A – C]
∴ AC + AB = 9.8 cm …[From (i) and (ii)]
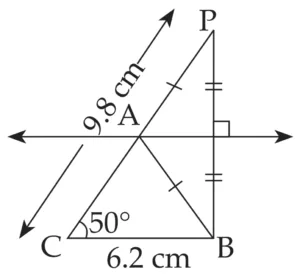
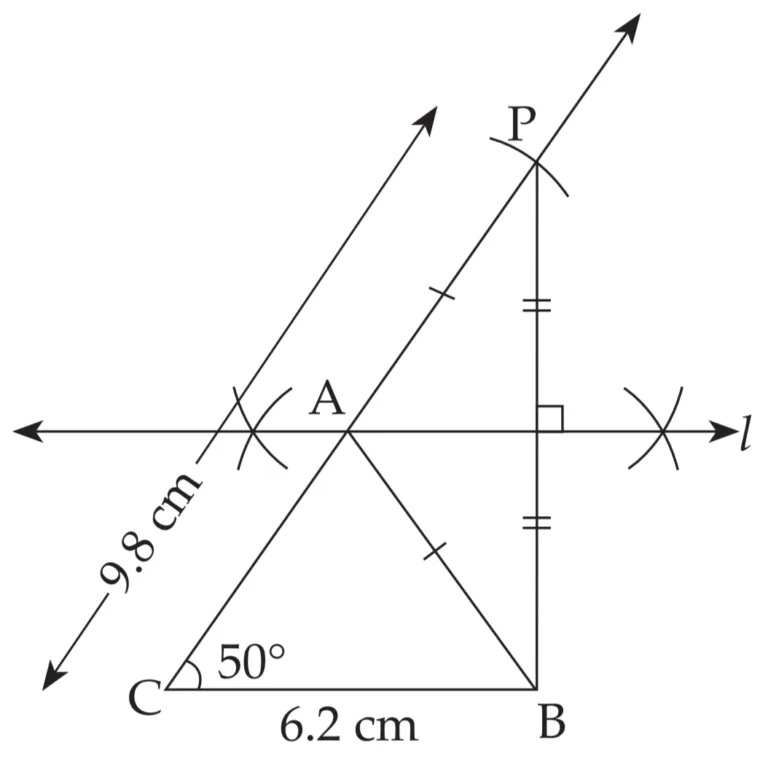
This is the required construction.
4. Construct ∆ABC, in which BC = 3.2 cm, ∠ACB = 45° and perimeter of ∆ABC is 10 cm.
Solution:
Perimeter of ∆ABC = AB + BC + AC
∴ AB + AC + 5.2 = 15 cm
∴ AB + AC = 15 – 5.2
∴ AB + AC = 9.8 cm
Explanation:
Line l is perpendicular bisector of seg PB
∴ AP = AB …(i) [Perpendicular bisector theorem]
PC = 9.8 cm …(ii)
AP + AC = PC …[P – A – C]
∴ AB + AC = 9.8 cm …[From (i) and (ii)]
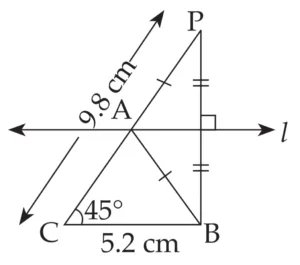
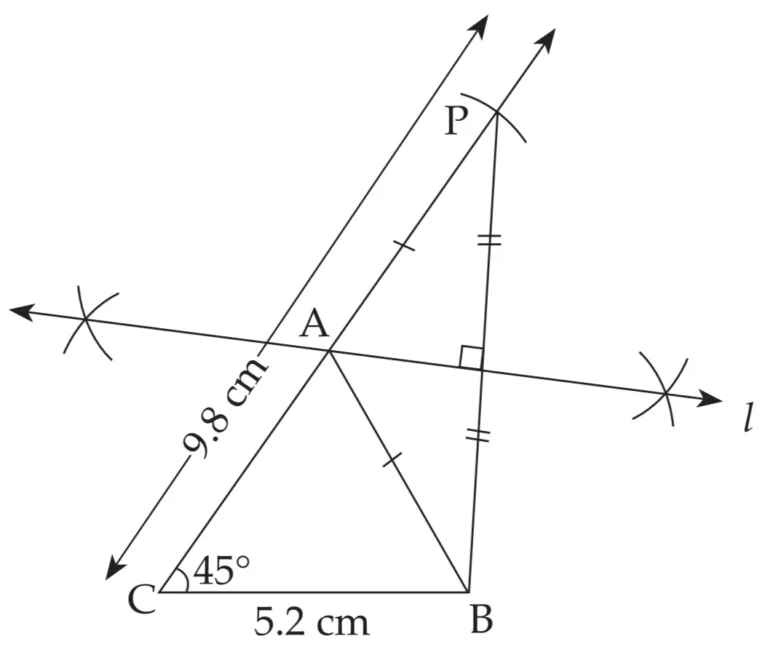
This is the required construction.
Practice set 4.2
1. Construct ∆XYZ, such that YZ = 7.4 cm, ∠XYZ = 45° and XY – XZ = 2.7 cm.
Explanation:
Line l is perpendicular bisector of seg PZ
∴ XP = XZ …(i) [Perpendicular bisector theorem]
PY = 2.7 cm …(ii)
XY = XP + PY ...[X – P – Y]
∴ XY = XZ + 2.7 cm ...[From (i) and (ii)]
∴ XY – XZ = 2.7 cm
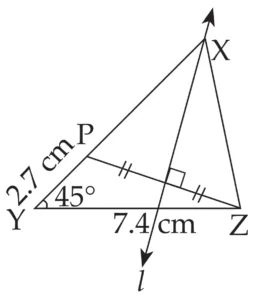
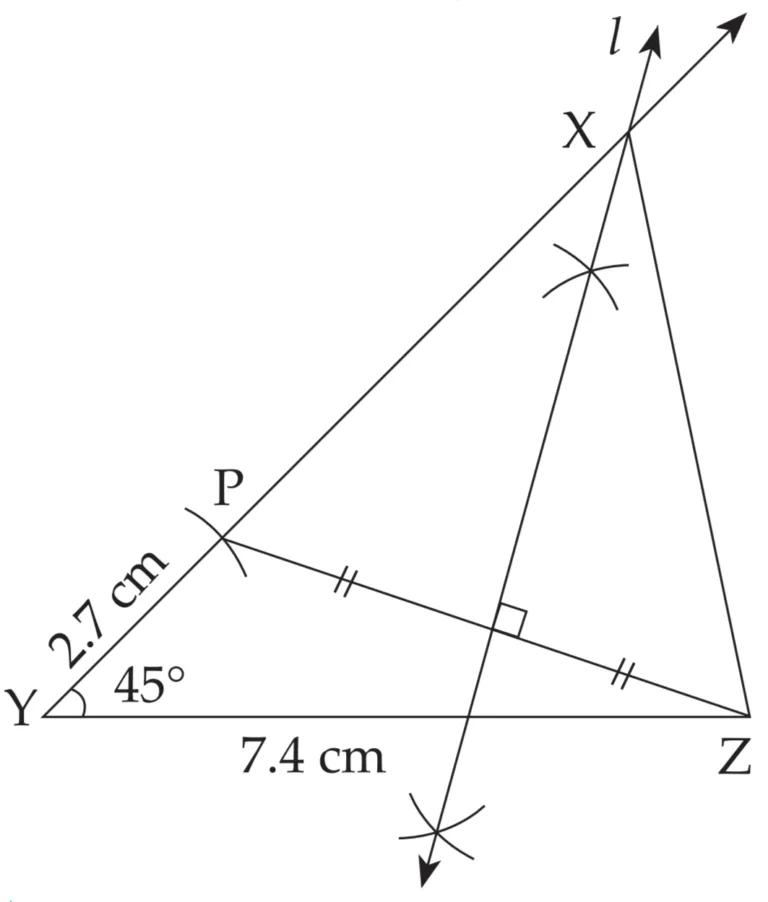
This is the required construction.
2. Construct ∆PQR, such that QR = 6.5 cm, ∠PQR = 40° and PQ – PR = 2.5 cm.
Explanation:
Line l is perpendicular bisector of seg MR
∴ PM = PR …(i) [Perpendicular bisector theorem]
QM = 2.5 cm …(ii)
PQ = PM + QM …[P – M – Q]
∴ PQ = PR + 2.5 …[From (i) and (ii)]
∴ PQ – PR = 2.5 cm
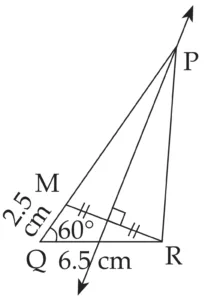
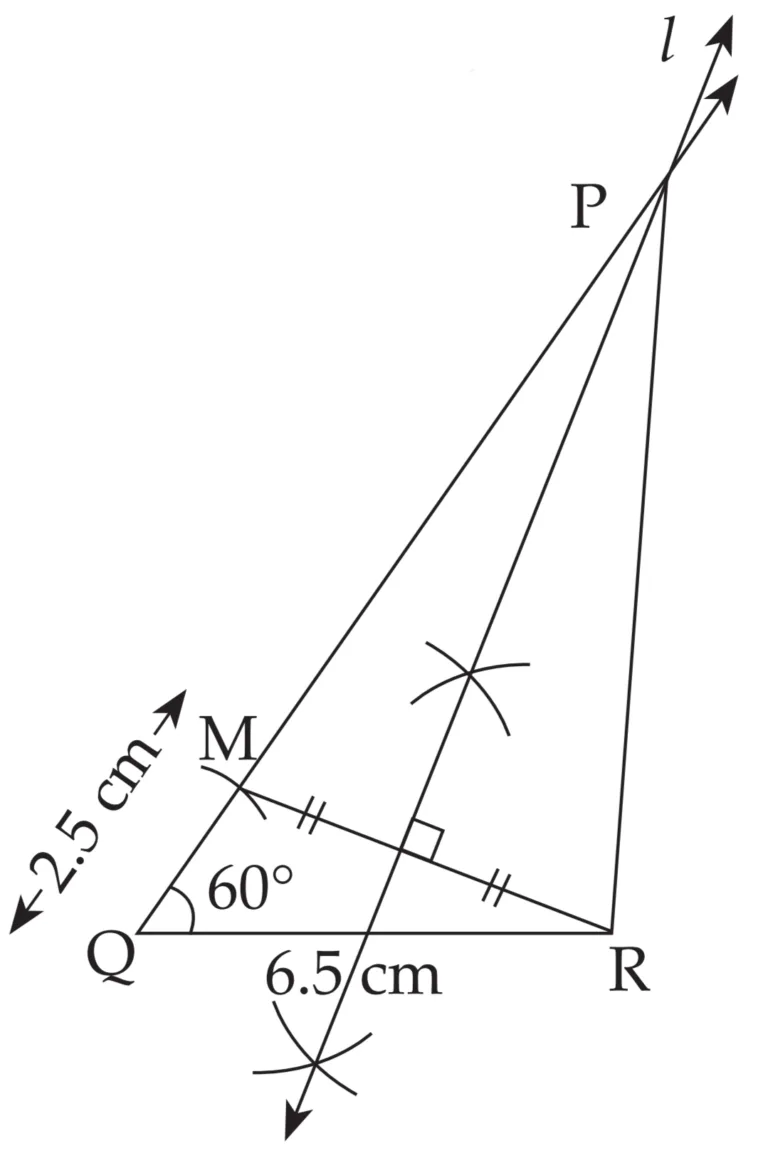
This is the required construction.
3. Construct ∆ABC, such that BC = 6 cm, ∠ABC = 100° and AC – AB = 2.5 cm.
Explanation:
Line l is perpendicular bisector of seg MC
∴ AM = AC …(i) [Perpendicular bisector theorem]
BM = 2.5 cm … (ii)
AM = AB + BM …[A – B – M]
∴ AC = AB + 2.5 cm ...[From (i) and (ii)]
∴ AC – AB = 2.5 cm
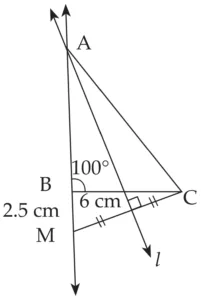
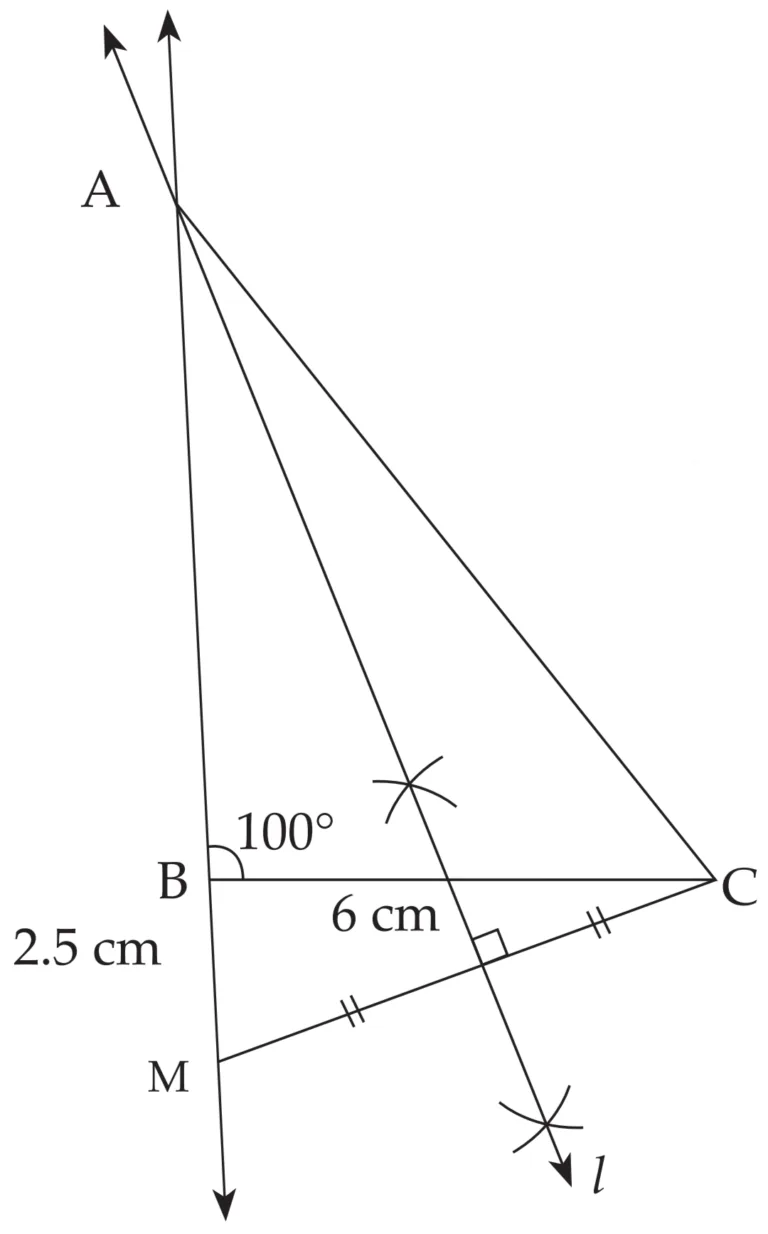
This is the required construction.
Practice set 4.3
1. Construct ∆PQR, in which ∠Q = 70°, ∠R = 80° and PQ + QR + PR = 9.5 cm.
Explanation:
Line l and m are perpendicular bisector of seg PA and PB respectively
∴ PQ = AQ and PR = RB …(i) [Perpendicular bisector theorem]
PQ + QR + PR = 9.5 cm
∴ AQ + QR + RB = 9.5 cm
∴ AB = 9.5 cm
In ∆PQA,
seg PQ ≅ seg AQ …[From (i)]
∴ ∠QPA ≅ ∠QAP …[Isosceles triangle theorem]
Let ∠QPA = ∠QAP = x
∠PQR is an exterior angle of ∆PQA
∴ ∠QPA + ∠QAP = ∠PQR …[Remote interior angle theorem]
∴ x + x = 70
∴ 2x = 70
∴ x = 35
∴ ∠QPA = ∠QAP = 35°
Similarly, we can prove
∠RPB = ∠RBP = 40°
Now, draw ∆ PAB, with AB = 9.5 cm, ∠A = 35° and ∠B = 40°
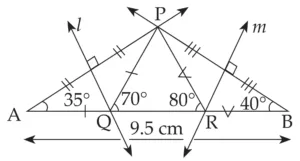
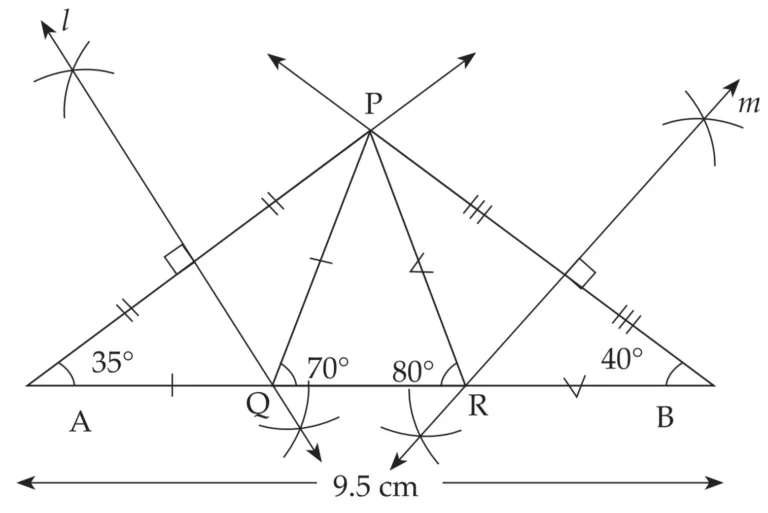
This is the required construction.
2. Construct ∆XYZ, in which ∠Y = 58°, ∠X = 46° and the perimeter of the triangle is 10.5 cm.
Explanation:
Line l and m are perpendicular bisector of seg PZ and QZ respectively
∴ PX = ZX and ZY = QY …(i) [Perpendicular bisector theorem]
XY + YZ + XZ = 10.5 cm …[Given]
∴ XY + QY + PX = 10.5 cm ...[From (i) and (ii)]
∴ PQ = 10.5 cm …[P – X – Y – Q]
In ∆PXZ,
seg PX ≅ seg ZX …[From (i)]
∴ ∠XPZ ≅ ∠XZP …[Isosceles triangle theorem]
Let ∠XPZ = ∠XZP = x
∠ZXY is an exterior angle of ∆PXZ
∴ ∠ZXY = ∠XPZ + ∠XZP …[Remote interior angle theorem]
∴ 46 = x + x
∴ 46 = 2x
∴ x = 23
∴ ∠XPZ = ∠XZP = 23°
Similarly,
we can prove ∠YQZ = ∠YZQ = 29°.
Now, draw ∆ZPQ, with PQ = 10.5 cm, ∠P = 23° and ∠Q = 29°
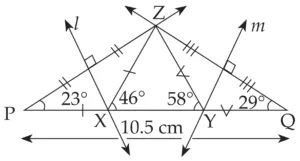
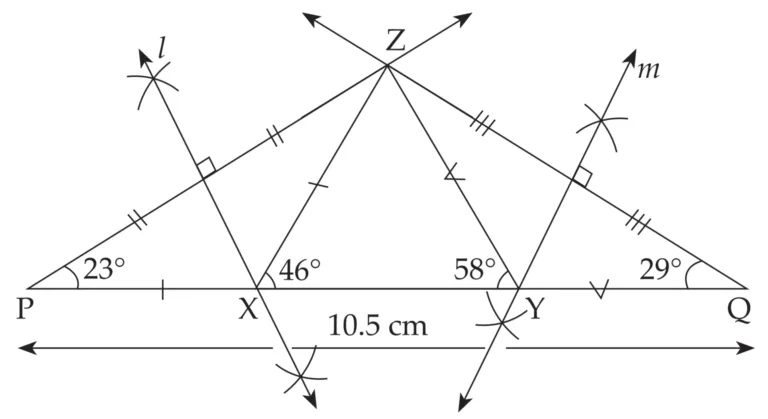
This is the required construction.
3. Construct ∆LMN, in which ∠M = 60°, ∠N = 80° and LM + MN + NL = 11 cm.
Explanation:
Line l and m are perpendicular bisector of seg PL and seg LQ respectively
∴ MP = ML and NL = NQ …(i) [Perpendicular bisector theorem]
LM + MN + NL = 11 cm …[Given]
∴ MP + MN + NQ = 11 cm ...[From (i) and (ii)]
∴ PQ = 11 cm …[P – M – N – Q]
In ∆PML,
∴ seg MP ≅ seg ML …[From (i)]
∠MPL ≅ ∠MLP …[Isosceles triangle theorem]
Let ∠MPL = ∠MLP = x
∠LMN is an exterior angle of ∆PML
∴ ∠LMN = ∠MPL + ∠MLP …[Remote interior angle theorem]
∴ 60 = x + x
∴ 60 = 2x
∴ x = 30
∴ ∠MPL = ∠MLP = 30°
Similarly,
we can prove ∠NQL = ∠NLQ = 40°.
Now, draw ∆LPQ, with PQ = 11 cm, ∠P = 30° and ∠Q = 40°
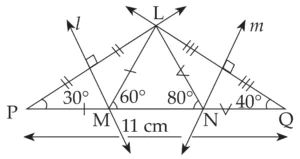
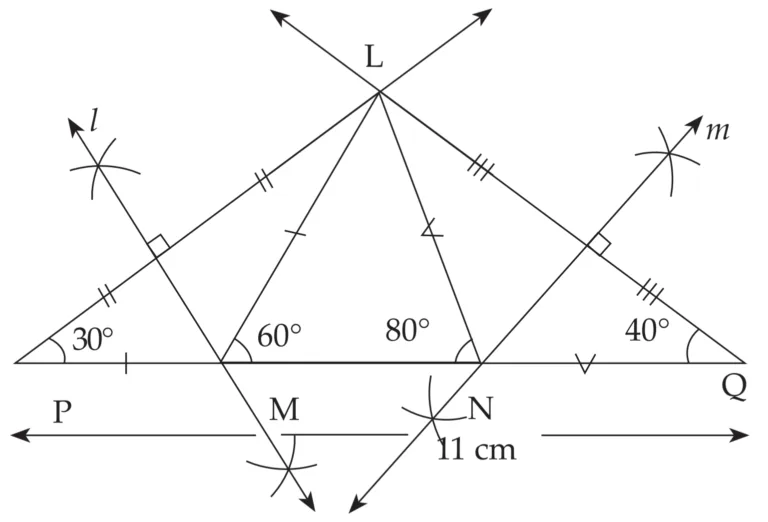
This is the required construction.
This is the required construction.
Problem Set 4
1. Construct ∆XYZ, such that XY + XZ = 10.3 cm, YZ = 4.9 cm, ∠XYZ.
Explanation:
Line l is perpendicular bisector of seg PZ
∴ XP = XZ …(i) [Perpendicular bisector theorem]
PY = 10.3 cm …(ii)
XY + XP = PY …[P – X – Y]
∴ XY + XZ = 10.3 cm …[From (i) and (ii)]
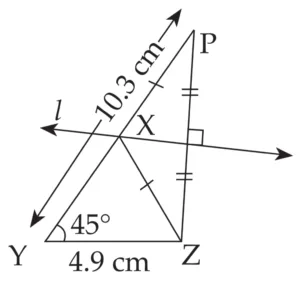
This is the required construction.
2. Construct ∆ABC, in which ∠B = 70°, ∠C = 60°, AB + BC + AC = 11.2 cm.
Explanation:
Line l and m are perpendicular bisector of seg AP and AQ respectively
∴ BP = BA …(i) and CQ = CA …(ii) [Perpendicular bisector theorem]
AB + BC + AC = 11.2 cm …[Given]
∴ BP + BC + CQ = 11.2 cm …[From (i), (ii)]
∴ PQ = 11.2 cm …[P – B – C – Q]
In ∆ABP,
seg BP ≅ seg BA ...[From (i)]
∴ ∠BPA ≅ ∠BAP …[Isosceles triangle theorem]
Let ∠BPA = ∠BAP = x
∠ABC is an exterior angle of ∆ABP
∴ ∠ABC = ∠BPA + ∠BAP …[Remote interior angle theorem]
∴ 70 = x + x
∴ 70 = 2x
∴ x = 35
∴ ∠BPA = ∠BAP = 35°
Similarly,
we can prove ∠CAQ = ∠CQA = 30°.
Now, draw ∆APQ, with PQ = 11.2 cm, ∠P = 35° and ∠Q = 30°
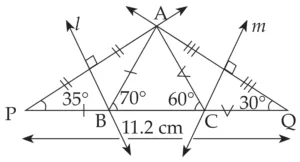
This is the required construction.
3. The perimeter of a triangle is 14.4 cm and the ratio of lengths of its side is 2 : 3 : 4. Construct the triangle.
Explanation:
Let the required triangle be ∆ABC.
AB + BC + AC = 14.4 …[Given]
AB : BC : AC = 2 : 3 : 4 …[Given]
Let the common multiple be x
∴ 2x + 3x + 4x = 14.4
∴ 9x = 14.4
∴ x = \(\large \frac {14.4}{9}\)
∴ x = 1.6
∴ AB = 2x = 2 × 1.6 = 3.2 cm
∴ BC = 3x = 3 × 1.6 = 4.8 cm
∴ AC = 4x = 4 × 1.6 = 6.4 cm
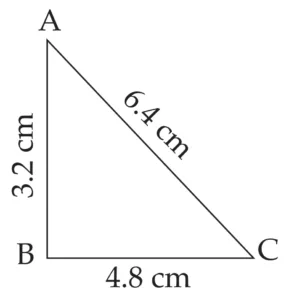
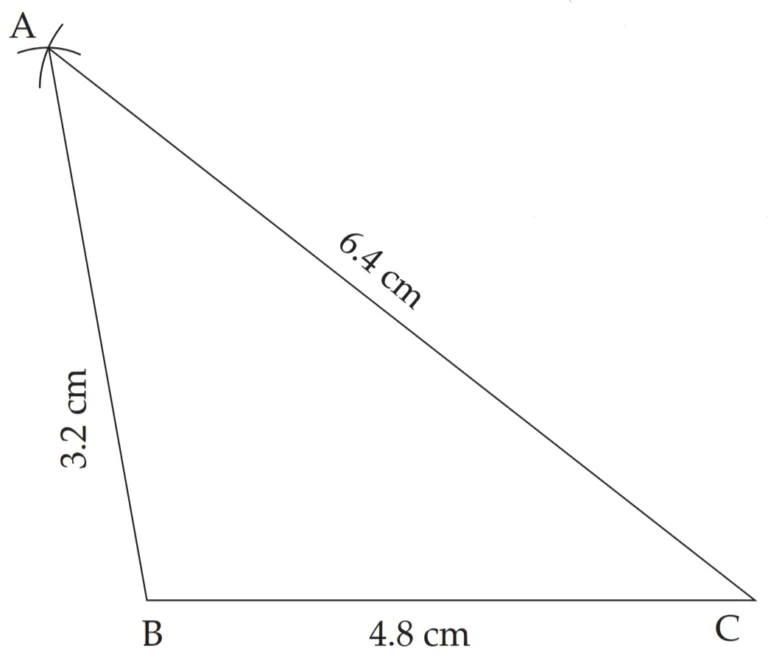
This is the required construction.
4. Construct ∆PQR, in which PQ – PR = 2.4 cm, QR = 6.4 cm and ∠PQR = 55°.
Explanation:
Line l is perpendicular bisector of seg TR
∴ PT = PR …(i) and QT = 2.4 cm …(ii) [Perpendicular bisector theorem]
PQ = PT + QT ...[P – T – Q]
∴ PQ = PR + 2.4 …[From (i) and (ii)]
∴ PQ – PR = 2.4 cm
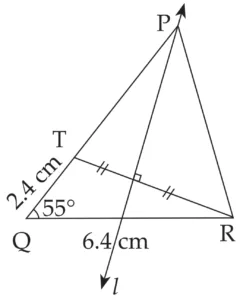
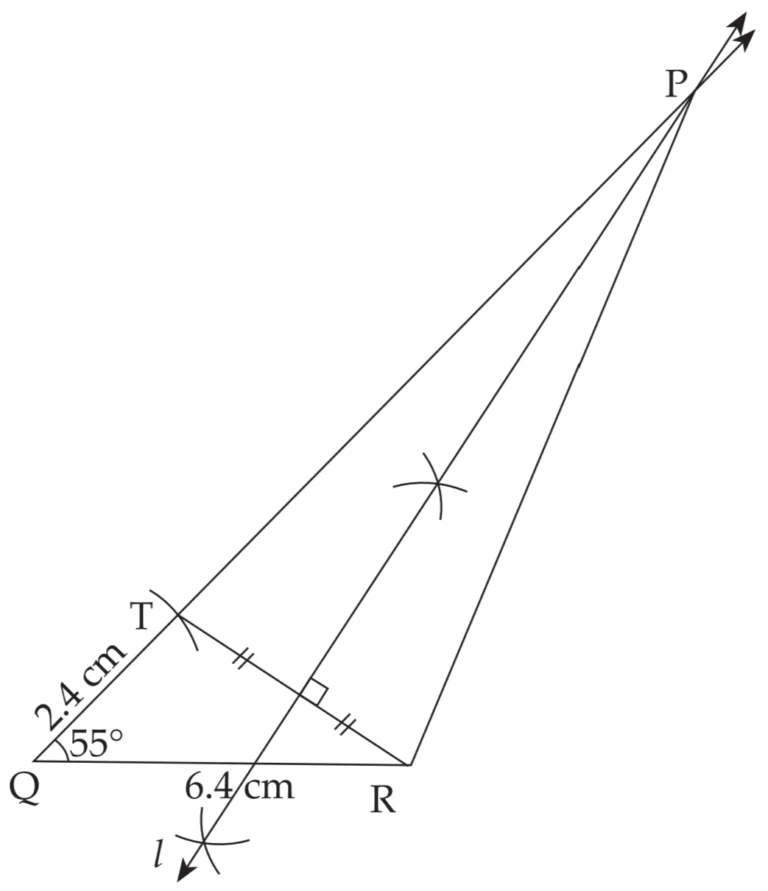
This is the required construction.
