Chapter 4 – Angles and Pairs of Angles
Practice Set 15
1. Observe the figure and complete the table for ∠AWB.
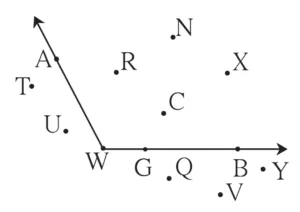

Ans:
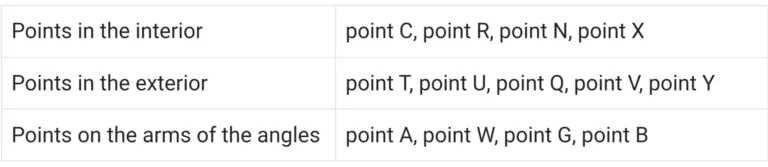
2. Name the pairs of adjacent angles in the figures below.
(i)
Ans:
∠ANB and ∠ANC
∠BNA and ∠BNC
∠ANC and ∠BNC
(ii)
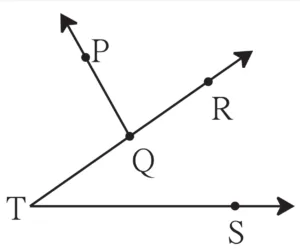
Ans: ∠PQR and ∠PQT
3. Are the following pairs adjacent angles? If not, state the reason.
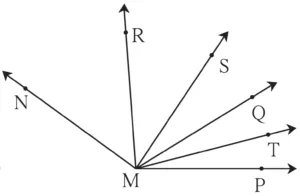
(i) ∠PMQ and ∠RMQ
Ans: ∠PMQ and ∠RMQ are adjacent angles.
(ii) ∠RMQ and∠SMR
Ans: ∠RMQ and ∠SMR not adjacent angles since they do not have separate interiors.
(iii) ∠RMS and ∠RMT
Ans: ∠RMS and ∠RMT not adjacent angles since they do not have separate interiors.
(iv) ∠SMT and ∠RMS
Ans: ∠SMT and ∠RMS are adjacent angles.
Practice set 16
1. The measures of some angles are given below. Write the measures of their complementary angles.
(i) 40°
Solution:
Let the measure of the complementary angle be x°.
∴ 40 + x = 90
∴ x = 90 – 40
∴ x = 50
Ans: The measure of the complement of an angle of measure 40° is 50°.
(ii) 63°
Solution:
Let the measure of the complementary angle be x°.
∴ 63 + x = 90
∴ x = 90 – 63
∴ x = 27
Ans: The measure of the complement of an angle of measure 63° is 27°.
(iii) 45°
Solution:
Let the measure of the complementary angle be x°.
∴ 45 + x = 90
∴ x = 90 – 45
∴ x = 45
Ans: The measure of the complement of an angle of measure 45° is 45°.
(iv) 55°
Solution:
Let the measure of the complementary angle be x°.
∴ 55 + x = 90
∴ x = 90 – 55
∴ x = 35
Ans: The measure of the complement of an angle of measure 55° is 35°.
(v) 20°
Solution:
Let the measure of the complementary angle be x°.
∴ 20 + x = 90
∴ x = 90 – 20
∴ x = 70
Ans: The measure of the complement of an angle of measure 20° is 70°.
(vi) 90°
Solution:
Let the measure of the complementary angle be x°.
∴ 90 + x = 90
∴ x = 90 – 90
∴ x = 0
Ans: The measure of the complement of an angle of measure 90° is 0°.
(vii) x°
Solution:
Let the measure of the complementary angle be a°.
∴ x + a = 90
∴ a = (90 – x)⁰
Ans: The measure of the complement of an angle of measure x° is (90 – x)°.
2. (y – 20)° and (y + 30)° are the measures of complementary angles. Find the measure of each angle.
Solution:
(y – 20)° and (y + 30)° are the measures of complementary angles.
∴ (y – 20) + (y + 30) = 90
∴ y – 20 + y + 30 = 90
∴ y + y + 30 – 20 = 90
∴ 2y + 10 = 90
∴ 2y = 90 – 10
∴ 2y = 80
∴ y = \(\large \frac {80}{2}\)
∴ y = 40
∴ (y – 20)° = (40 – 20)° = 20°
and (y + 30)° = (40 + 30)° = 70°
Ans: The measure of the two angles is 20° and 70°.
Practice set 17
1. Write the measures of the supplements of the angles given below.
(i) 15°
Solution:
Let the measure of the supplementary angle be x°.
∴ 15 + x = 180
∴ x = 180 – 15
∴ x = 165
Ans: The measure of the supplement of an angle of 15° is 165°.
(ii) 85°
Solution:
Let the measure of the supplementary angle be x°.
∴ 85 + x = 180
∴ x = 180 – 85
∴ x = 95
Ans: The measure of the supplement of an angle of 85° is 95°.
(iii) 120°
Solution:
Let the measure of the supplementary angle be x°.
∴ 120 + x = 180
∴ x = 180 – 120
∴ x = 60
Ans: The measure of the supplement of an angle of 120° is 60°.
(iv) 37°
Solution:
Let the measure of the supplementary angle be x°.
∴ 37 + x = 180
∴ x = 180 – 37
∴ x = 143
Ans: The measure of the supplement of an angle of 37° is 143°.
(v) 108°
Solution:
Let the measure of the supplementary angle be x°.
∴ 108 + x = 180
∴ x = 180 – 108
∴ x = 72
Ans: The measure of the supplement of an angle of 108° is 72°.
(vi) 0°
Solution:
Let the measure of the supplementary angle be x°.
∴ 0 + x = 180
∴ x = 180
Ans: The measure of the supplement of an angle of 0° is 180°.
(vii) a°
Solution:
Let the measure of the supplementary angle be x°.
∴ a + x = 180
∴ x = (180 – a)⁰
Ans: The measure of the supplement of an angle of a° is (180 – a)⁰.
2. The measures of some angles are given below. Use them to make pairs of complementary and supplementary angles.
m∠B = 60°
m∠N = 30°
m∠Y = 90°
m∠J = 150°
m∠D = 75°
m∠E = 0°
m∠F = 15°
m∠G = 120°
Solution:
(i) m∠B + m∠N
= 60° + 30°
= 90°
∴ ∠B and ∠N are a pair of complementary angles.
(ii) m∠Y + m∠E
= 90° + 0°
= 90°
∴ ∠Y and ∠E are a pair of complementary angles.
(iii) m∠D + m∠F = 75° + 15°
= 90°
∴ ∠D and ∠F are a pair of complementary angles.
(iv) m∠B + m∠G
= 60° + 120°
= 180°
∴ ∠B and ∠G are a pair of supplementary angles.
(v) m∠N + m∠J
= 30° + 150°
= 180°
∴ ∠N and ∠J are a pair of supplementary angles.
3. In ∆XYZ, m∠Y = 90°. What kind of a pair do ∠X and ∠Z make?
Solution:
In ∆ XYZ,
m∠X + m∠Y + m∠Z = 180° …[Sum of the measure of the angles of a triangle is 180°]
∴ m∠X + 90 + m∠Z = 180
∴ m∠X + m∠Z = 180 – 90
∴ m∠X + m∠Z = 90°
Ans: ∠X and ∠Z make a pair of complementary angles.
4. The difference between the measures of the two angles of a complementary pair is 40°. Find the measures of the two angles.
Solution:
Let the measure of one angle be x°.
∴ Measure of other angle = (90 – x)⁰
According to the given condition,
x – (90 – x) = 40
∴ x – 90 + x = 40
∴ 2x – 90 = 40
∴ 2x = 40 + 90
∴ 2x = 130
∴ x = \(\large \frac {130}{2}\)
∴ x = 65⁰
∴ (90 – x)⁰ = 90 – 65 = 25⁰
Ans: The measures of the two angles are 65° and 25°.
5. □ PTNM is a rectangle. Write the names of the pairs of supplementary angles.

Solution:
Each angle of the rectangle is 90°.
∴ The pairs of supplementary angles are:
(i) ∠P and ∠M
(ii) ∠P and ∠N
(iii) ∠P and ∠T
(iv) ∠M and ∠N
(v) ∠M and ∠T
(vi) ∠N and ∠T
6. If m∠A = 70°, what is the measure of the supplement of the complement of ∠A?
Solution:
Let the measure of the complement of ∠A be x°
m∠A + x = 90°
∴ 70 + x = 90
∴ x = 90 – 70
∴ x = 20
Let the measure of the supplementary of the complementary angle be y°.
Since, x and y are supplementary angles.
∴ x + y = 180
∴ 20 + y = 180
∴ y = 180 – 20
∴ y = 160⁰
Ans: The measure of supplement of the complement of ∠A is 160°.
7. If ∠A and ∠B are supplementary angles and m∠B = (x + 20)°, then what would be m∠A?
Solution:
∠A and ∠B are supplementary angles.
∴ m∠A + m∠B = 180
∴ m∠A + (x + 20) = 180
∴ m∠A + x = 180 – 20
∴ m∠A + x = 160
∴ m∠A = (160 – x)°
Ans: The measure of ∠A is (160 – x)°.
Practice set 18
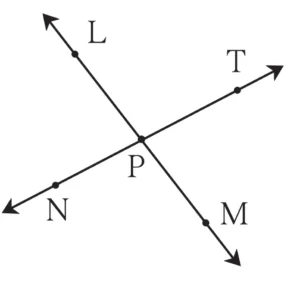
1. Name the pairs of opposite rays in the figure alongside.
Ans:
Ray PN and ray PT
Ray PL and ray PM
2. Are the ray PM and PT opposite rays? Give reasons for your answer.
Ans: No, Ray PM and PT are not opposite rays. Ray PM and Ray PT do not form a straight line and hence are not opposite rays.
Practice set 19
Draw the pairs of angles as described below. If that is not possible, say why
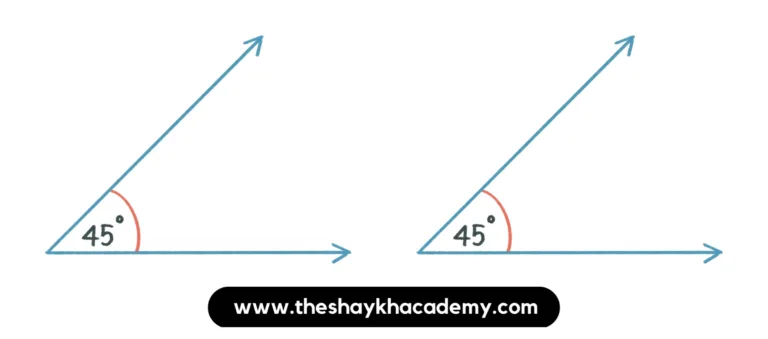
(i) Complementary angles that are not adjacent.
Ans:
(ii) Angles in a linear pair which are not supplementary.
Ans: Sum of angles in a linear pair is 180° i.e. they are supplementary .
∴ Angles in a linear pair which are not supplementary cannot be drawn.
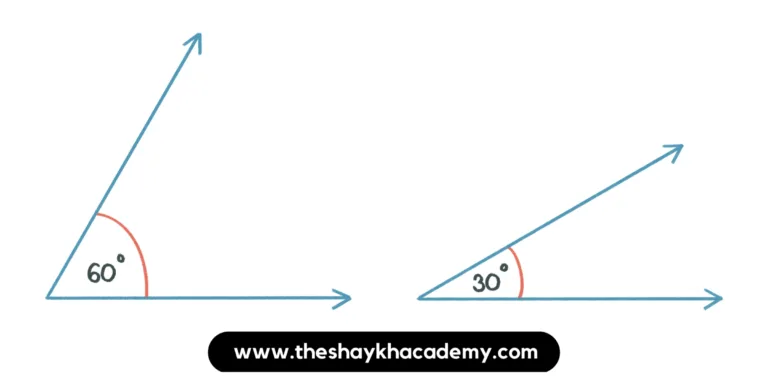
(iii) Complementary angles that do not form a linear pair.
Ans:
(iv) Adjacent angles which are not in a linear pair.
Ans:
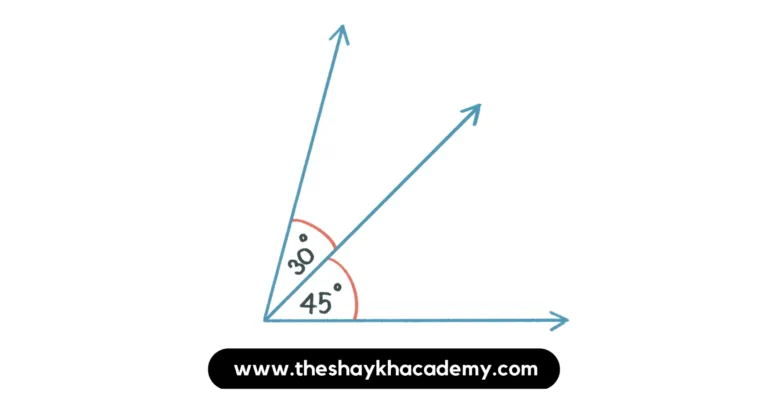
(v) Angles which are neither complementary nor adjacent.
Ans:
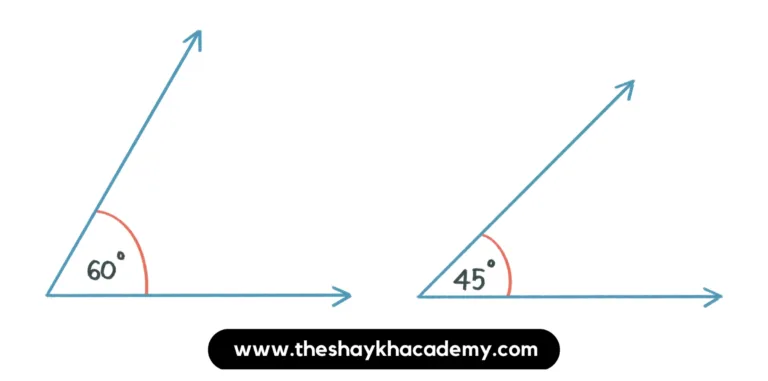
(vi) Angles in a linear pair which are complementary.
Ans: Sum of angles in linear pair is 180°, but the sum of complementary angles is 90°.
∴ Angles in a linear pair which are complementary cannot be drawn.
Practice set 20
1. Lines AC and BD intersect at point P. m∠APD = 47°. Find the measures of ∠APB, ∠BPC, ∠CPD.
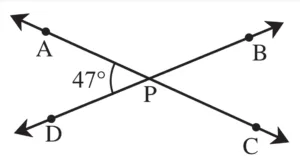
Solution:
∠APD and ∠APB are angles in a linear pair.
∴ m∠APD + m∠APB = 180°
∴ 47 + m∠APB = 180
∴ m∠APB = 180 – 47
∴ m∠APB = 133°
Now,
m∠CPD ≅ m∠APB …[Vertically opposite angles]
∵ m∠APB = 133°
∴ m∠CPD = 133⁰
m∠BPC ≅ m∠APD = 47° …[Vertically opposite angles]
∵ m∠APD = 47°
∴ m∠BPC = 47⁰
Ans: The measures of ∠APB, ∠BPC and ∠CPD are 133°, 47° and 133° respectively.
2. Lines PQ and RS intersect at point M. m∠PMR = x°. What are the measures of ∠PMS, ∠SMQ and ∠QMR?
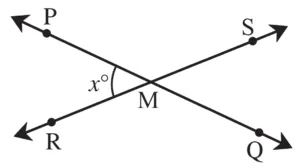
Solution:
∠PMR and ∠PMS are angles in a linear pair.
∴ m∠PMR + m∠PMS = 180°
∴ x + m∠PMS = 180
∴ m∠PMS = (180 – x)°
Now,
m∠QMR ≅ m∠PMS …[Vertically opposite angles]
∵ m∠PMS = (180 – x)°
∴ m∠QMR = (180 – x)°
m∠SMQ ≅ m∠PMR …[Vertically opposite angles]
∵ m∠PMR = x
∴ m∠SMQ = x
Ans: The measures of ∠PMS, ∠SMQ and ∠QMR are (180 – x)°, x° and (180 – x)° respectively.
Practice set 21
1. ∠ACD is an exterior angle of ∆ABC. The measures of ∠A and ∠B are equal. If m∠ACD = 140°, find the measures of the angles ∠A and ∠B.
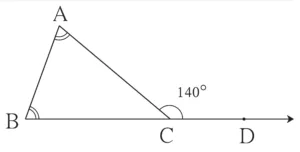
Solution:
Let the measure of ∠A be x°.
∴ m∠A = m∠B = x°
∠ACD is the exterior angle of ∆ABC
∴ m∠ACD = m∠A + m∠B
∴ 140 = x + x
∴ 2x = 140
∴ x = \(\large \frac {140}{2}\)
∴ x = 70
∴ m∠A = m∠B = x° = 70⁰
Ans: The measures of the angles ∠A and ∠B is 70° each.
2. Using the measures of the angles given in the figure alongside, find the measures of the remaining three angles.
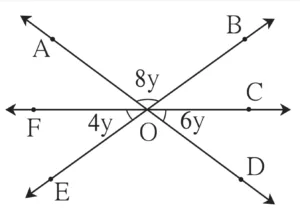
Solution:
m∠EOD ≅ m∠AOB …[Vertically opposite angles]
∵ m∠AOB = 8y
∴ m∠EOD = 8y
m∠AOF ≅ m∠COD …[Vertically opposite angles]
∵ m∠COD = 6y
∴ m∠AOF = 6y
m∠BOC ≅ m∠FOE …[Vertically opposite angles]
∵ m∠FOE = 6y
∴ m∠BOC = 6y
∠FOL, ∠EOD and ∠COD form a straight angle.
∴ m∠FOE + m∠EOD + m∠COD = 180°
∴ 4y + 8y + 6y = 180
∴ 18y = 180
∴ y = \(\large \frac {180}{18}\)
∴ y = 10
m∠EOD = 8y = 8 × 10 = 80°
m∠AOF = 6y = 6 × 10 = 60°
m∠BOC = 4y = 4 × 10 = 40°
Ans: The measures of ∠EOD, ∠AOF and ∠BOC are 80°, 60° and 40° respectively.
3 . In the isosceles triangle ABC, ∠A and ∠B are equal. ∠ACD is an exterior angle of ∆ABC. The measures of ∠ACB and ∠ACD are (3x – 17)° and (8x + 10)° respectively. Find the measures of ∠ACB and ∠ACD. Also find the measures of ∠A and ∠B.
Solution:
Let the measure of ∠A be y°
∴ m∠A = m∠B = y°
∠ACB and ∠ACD form a pair of linear angles.
∴ m∠ACB + m∠ACD = 180°
∴ (3x – 17) + (8x + 10) = 180
∴ 3x + 8x – 17 + 10 = 180
∴ 11x – 7 = 180
∴ 11x = 180 + 7
∴ 11x = 187
∴ x = \(\large \frac {187}{11}\)
∴ x = 17
m∠ACB = 3x – 17
∴ m∠ACB = (3 × 17) – 17
∴ m∠ACB = 51 – 17
∴ m∠ACB = 34°
m∠ACD = 8x + 10
∴ m∠ACD = 8 × 17 + 10
∴ m∠ACD = 136 + 10
∴ m∠ACD = 146°
Here ∠ACD is the exterior angle of ∆ABC and ∠A and ∠B are its remote interior angles.
∴ m∠ACD = m∠A + m∠B
∴ 146 = y + y
∴ 146 = 2y
∴ 2y = 146
∴ y = \(\large \frac {146}{2}\)
∴ y = 73⁰
Ans: The measures of ∠ACB, ∠ACD, ∠A and ∠B are 34°, 146°, 73° and 73° respectively.
