Chapter 1 – Sets
Practice set 1.1
(1) Write the following sets in the roster form:
(i) Set of even natural numbers
Solution:
A = { 2, 4, 6, 8, … }
(ii) Set of even prime numbers from 1 to 50
Solution:
B = { 2 }
(iii) Set of negative integers
Solution:
C = { –1, –2, –3, … }
(iv) Seven basic sounds of a sargam (sur)
Solution:
D = { sa, re, ga, ma, pa, dha, ni }
(2) Write the following symbolic statement in words:
(i) \(\large \frac {4}{3}\) ∈ Q
Solution:
\(\large \frac {4}{3}\) belong to the set Q.
or
\(\large \frac {4}{3}\) is an element of the set Q.
(ii) – 2 ∉ N
Solution:
– 2 does not belong to the set N
or
– 2 is not an element of the set N.
(iii) P = { p | p is an odd number }
Solution:
P is the set of all p such that p is an odd number.
(3) Write two sets by listing method and by rule method:
Solution:
Roster form
A = { 1, 4, 9, 16, 25, 36, 49 }
B = { 2, 3, 5, 7, 11, 13, 17, 19 }
Set Builder form
A = { x | x is a number such that y² = 9 }
B = { y | y ∈ I, –3 < y < 3 }
(4) Write the following sets using the listing method:
(i) All months in the Indian solar year.
Solution:
A = { Chaitra, Vaishakh, Jyeshth, Ashadh, Shravan, Bhadra, Ashwin, Kartik, Agrahayan, Paush, Magh, Phalgun }
(ii) Letters in the word ‘COMPLEMENT’.
Solution:
B = { C, O, M, P, L, E, N, T }
(iii) Set of human sensory organs.
Solution:
C = { ear, nose, tongue, skin, eye }
(iv) Set of prime numbers from 1 to 20.
Solution:
D = { 2, 3, 5, 7, 11, 13, 17, 19 }
(v) Names of continents of the world.
Solution:
E = { Asia, Africa, North America, South America, Europe, Antarctica, Australia }
(5) Write the following sets using rule method:
(i) A = { 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 }
Solution:
A = { x | x = n², n ∈ N, n < 10 }
(ii) B = { 6, 12, 18, 24, 30, 36, 42, 48 }
Solution:
B = { y | y = 6n, n ∈ N, n < 8 }
(iii) C = { S, M, I, L, E }
Solution:
C = { x | x is a letter of the word SMILE }
(iv) D = { Sunday, Monday, Tuesday, Wednesday, Friday, Saturday }
Solution:
D = { y | y is a day in a week }
(v) X = { a, e, t }
Solution:
X = { y | y is a letter of the word eat }
or
X = { y | y is a letter of the word tea }
Practice set 1.2
(1) Decide which of the following are equal sets and which are not? Justify your answer.
A = { x | 3x – 1 = 2 }
B = { x | x is a natural number but x is neither prime nor composite }
C = { x | x ∈ N, x < 2 }
Solution:
A = { x | 3x – 1 = 2 }
∴ A = { 1 }
B = { x | x is a natural number but x is neither prime nor composite }
∴ B = { 1 }
C = { x | x ∈ N, x < 2 }
∴ C = { 1 }
Here elements of sets A, B and C are exactly same
∴ A = B = C
(2) Decide whether set A and B are equal sets. Give reason for your answer.
A = Even prime numbers
B = { x | 7x – 1 = 13 }
Solution:
A = Even prime numbers
∴ A = { 2 }
B = { x | 7x – 1 = 13 }
∴ B = { 2 }
Here elements of A and B are exactly same.
∴ A = B
(3) Which of the following are empty sets? Why?
(i) A = { a | a is a natural number smaller than zero }
Solution:
A = { a | a is a natural number less than zero }
∴ A = { }
∴ Set A is an empty set as it does not have any element.
(ii) B = { x | x² = 0 }
Solution:
B = { x | x² = 0 }
∴ B = { 0 }
∴ Set B is not an empty set as it contains one element
(iii) C = { x | 5x – 2 = 0, x ∈ N }
Solution:
C = { x | 5x – 2 = 0, x ∈ N }
∴ C = { }
∴ Set C is an empty set as it does not have any element.
(4) Write with reasons, which of the following sets are finite or infinite.
(i) A = { x | x < 10, x ∈ N }
Solution:
A = { 1, 2, 3, … , 9 }
∴ Set A is a finite set as it contains 9 elements.
(ii) B = { y | y < – 1, y ∈ I }
Solution:
B = { – 2, – 3, … }
∴ Set B is an infinite set as we cannot count its element.
(iii) C = Set of all the students of Std. 9 in your school.
Solution:
Set C is a finite set as we can count the number students of Std. 9.
(iv) Set of people living in a village.
Solution:
It is a finite set as we can count the number of people living in a village.
(v) Set of all apparatus used in the laboratory.
Solution:
It is a finite set as we can count the number of apparatus used in the laboratory.
(vi) Set of whole numbers.
Solution:
W = { 0, 1, 2, 3, … }
It is an infinite set as we can not count the number of its elements.
(vii) Set of rational numbers.
Solution:
Natural numbers, whole numbers, integers are all included in the set of rational numbers.
∴ It is an infinite set as we can not count number of its elements.
Practice set 1.3
(1) If A = {a, b, c, d, e,}, B = {c, d, e, f}, C = {b, d}, D = {a, e} then which of the following statements are true and which are false?
(i) C ⊆ B
Ans: False
(ii) A ⊆ D
Ans: False
(iii) D ⊆ B
Ans: False
(iv) D ⊆ A
Ans: True
(v) B ⊆ A
Ans: False
(vi) C ⊆ A
Ans: True
2) Take the set of natural numbers from 1 to 20 as a universal set and show set X and Y using the Venn diagram.
(i) X = { x | x ∈ N, 7 < x < 15 }
Solution:
X = { 1, 8, 9, 10, 11, 12, 13, 14 }

(ii) Y = { y | y ∈ N, y is a prime number between 1 to 20 }
Solution:
Y = { 2, 3, 5, 7, 11, 13, 17, 19 }

(3) U = { 1, 2, 3, 7, 8, 9, 10, 11, 12 } P = { 1, 3, 7, 10 } then,
(i) Draw Venn diagram for U, P and P’
(ii) Verify (P’)’ = P
Solution:
(i) U = { 1, 2, 3, 7, 8, 9, 10, 11, 12 }
P = { 1, 3, 7, 10 }
P’ = { 2, 8, 9, 11, 12 }
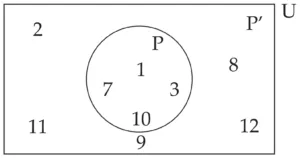
(ii) U = { 1, 2, 3, 7, 8, 9, 10, 11, 12 }
P = { 1, 3, 7, 10 } …(i)
P’ = { 2, 8, 9, 11, 12 }
∴ (P’)’ = { 1, 3, 7, 10 } …(ii)
∴ (P’)’ = P [From (i) and (ii)]
Hence proved.
(4) A = { 1, 3, 2, 7 }, write any three subsets of set A.
Solution:
The following sets are subsets of set A:
{ 1 }, { 2 }, { 3 }, { 7 }, { 1, 3 }, { 1, 2 }, { 1, 7 }, { 3, 2 }, { 3, 7 }, { 2, 7 }, { 1, 3, 2 }, { 1, 2, 7 }, { 3, 2, 7}, { 1, 3, 7 }, {1, 3, 2, 7}, φ
(5) (i) Write the subset relation between the sets.
P is the set of all residents in Pune.
M is the set of all residents in Madhya Pradesh.
I is the set of all residents in Indore.
B is the set of all residents in India.
H is the set of all residents in Maharashtra.
Solution:
P ⊆ H
P ⊆ B
I ⊆ M
I ⊆ B
H ⊆ B
M ⊆ B
(ii) Which set can be the universal set for the above sets?
Ans: Set B
Reason:
Pune, Madhya Pradesh, Indore, and Maharashtra are all either cities or states in India.
(6) Which set of numbers could be the universal set for the sets given below?
(i) A = set of multiples of 5,
B = set of multiples of 7,
C = set of multiples of 12.
Solution:
A = Set of multiples of 5
∴ A = { 5, 10, 15, 20 … }
B = Set of multiples of 7
∴ B = { 7, 14, 21, 28 … }
C = Set of multiples of 12
∴ C = { 12, 24, 36, 48 … }
We know that,
N = { 1, 2, 3, 4 … }
W = { 0, 1, 2, 3, 4 … }
I = { … –2, –1, 0, 1, 2 … }
∴ Considering the given three sets A, B and C, we can take natural numbers (N) or whole numbers (W) or Integers (I) as the universal set.
(ii) P = set of integers which are multiples of 4
T = set of all even square numbers
Solution:
P = Set of integers which are multiples of 4
∴ P = { 4, 8, 12, 16, … }
T = Set of all even square numbers
∴ T = { 4, 16, 36, 64 … }
We know that,
N = { 1, 2, 3 …}
W = { 0, 1, 2, 3 … }
I = { …, –1, 0, 1 … }
∴ For the two given sets P and T, we can take natural numbers (N) or whole numbers (W) or Integers (I) as Universal set.
(7) Let all the students of a class be a Universal set. Let set A be the students who secure 50% or more marks in Maths. Then write the complement of set A.
Solution:
U = The set of all students in a class.
A = The set of students scoring 50% and above in Maths from the given class.
∴ A’ = The set of students scoring less than 50% in Maths from the given class.
Practice set 1.4
(1) If n(A) = 15, n(A ∪ B) = 29, n(A ∩ B) = 7 then find n(B).
Solution:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
∴ 29 = 15 + n(B) – 7
∴ 29 = 8 + n(B)
∴ n(B) = 29 – 8
∴ n(B) = 21
Ans: The value of n(B) is 21.
(2) In a school hostel there are 125 students out of which 80 drink tea, 60 drink coffee and 20 drink both tea and coffee. Find the number of students who do not take tea or coffee.
Solution:
Total number of students in school hostel = 125
∴ n(U) = 125
Let T be the set of students who drink tea.
∴ n(T) = 80
Let C be the set of students who drink coffee.
∴ n(C) = 60
20 students drink both tea and coffee.
∴ n(T ∩ C) = 20
Now,
n(T ∪ C) = n(T) + n(C) – n(T ∩ C)
∴ n(T ∪ C) = 80 + 60 – 20
∴ n(T ∪ C) = 120
And,
n(T ∪ C) + n(T ∪ C)’ = n(U)
∴ n(T ∪ C)’ = n(U) – n(T ∪ C)
∴ n(T ∪ C)’ = 125 – 120
∴ n(T ∪ C)’ = 5
Ans: 5 students do not take tea or coffee.
(3) In a competitive exam 50 students passed in English. 60 students passed in Mathematics. 40 students passed in both the subjects. None of them fail in both the subjects. Find the number of students who passed at least in one of the subjects?
Solution:
Let E be the set of students who passed in English.
∴ n(E) = 50
Let M be the set of students who passed in Maths
∴ n(M) = 60
40 students passed in both subjects.
n(E ∩ M) = 40
The number of students who passed at least in one of the subjects = n(E ∪ M) = ?
n(E ∪ M) = n(E) + n(M) – n(E ∩ M)
∴ n(E ∪ M) = 50 + 60 – 40
∴ n(E ∪ M) = 70
Ans: 70 students passed in at least one of the subjects.
(4) A survey was conducted to know the hobbies of 220 students of class IX. Out of which 130 students informed about their hobby as rock climbing and 180 students informed about their hobby as sky watching. There are 110 students who follow both the hobbies. Then how many students do not have any of the two hobbies? How many of them follow the hobby of rock climbing only? How many students follow the hobby of sky watching only?
Solution:
Let U be the set of all surveyed students of Std. IX
∴ n(U) = 220
Let A be the set of students who like rock climbing.
∴ n(A) = 130
Let B be the set of students who like star watching.
∴ n(B) = 180
110 students like both rock climbing and star watching.
∴ n(A ∩ B) = 110
We know that,
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
∴ n(A ∪ B) = 130 + 180 – 110
∴ n(A ∪ B) = 200
Now,
n(A ∪ B) + n(A ∪ B)’ = n(U)
∴ n(A ∪ B)’ = n(U) – n(A ∪ B)
∴ n(A ∪ B)’ = 220 – 200
∴ n(A ∪ B)’ = 20
20 students do not like rock climbing or star watching.
Number of students who only like rock climbing,
= n(A) – n(A ∩ B)
= 130 – 110
= 20
20 students only like rock climbing.
Number of students who like only star watching,
= n(B) – n(A ∩ B)
= 180 – 110
= 70
70 students who like only star watching.
Ans: 20 students do not like rock climbing or star watching. 20 students follow the hobby of rock climbing only. 70 students follow the hobby of sky watching only.
(5) Observe the given Venn diagram and write the following sets.

(i) A
Solution:
A = { x, y, z, m, n }
(ii) B
Solution:
B = { p, q, r, m, n }
(iii) AB
Solution:
AB = { x, y, z, m, n, p, q, r }
(iv) U
Solution:
U = { x, y, z, m, n, p, q, r, s, t }
(v) A’
Solution:
A’ = { p, q, r, s, t }
(vi) B’
Solution:
B’ = { x, y, z, s, t }
(vii) (AB)’
Solution:
(AB)’ = { s, t }
Problem Set 1
(1) Choose the correct alternative answer for each of the following questions.
(i) M = { 1, 3, 5 }, N = { 2, 4, 6 } then M ∩ N = ?
(A) { 1, 2, 3, 4, 5, 6 }
(B) { 1, 3, 5 }
(C) φ
(D) { 2, 4, 6 }
Ans: Option (c) – φ
(ii) P = { x | x is an odd natural number, 1 < x < 5 }. How to write this set in roster form?
(A) {1, 3, 5}
(B) {1, 2, 3, 4, 5}
(C) {1, 3}
(D) {3, 5}
Ans: Option (D) – {3, 5}
(iii) P = {1, 2, ………., 10}, What type of set P is?
(A) Null set
(B) Infinite set
(C) Finite set
(D) None of these
Ans: Option (c) – Finite set
(iv) M ∪ N = {1, 2, 3, 4, 5, 6} and M = {1, 2, 4} then which of the following represent set N?
(A) {1, 2, 3}
(B) {3, 4, 5, 6}
(C) {2, 5, 6}
(D) {4, 5, 6}
Ans: Option (B) – {3, 4, 5, 6}
(v) If P ⊆ M, then which of the following set represent P ∩ (P ∪ M)?
(A) P
(B) M
(C) P ∪ M
(D) P’ ∩ M
Ans: Option (A) – P
(vi) Which of the following sets are empty sets?
(A) set of intersecting points of parallel lines
(B) set of even prime numbers.
(C) Month of an English calendar having less than 30 days.
(D) P = { x | x ∈ I, –1 < x < 1 }
Ans: Option (A) – set of intersecting points of parallel lines.
(2) Find the correct option for the given question.
(i) Which of the following collections is a set?
(A) Colours of the rainbow
(B) Tall trees on the school campus.
(C) Rich people in the village
(D) Easy examples in the book
Ans: Option (A) – Colours of the rainbow
(ii) Which of the following sets represent N ∩ W?
(A) {1, 2, 3, …}
(B) {0, 1, 2, 3, …}
(C) {0}
(D) { }
Ans: Option (A) – {1, 2, 3, …}
(iii) P = { x | x is a letter of the word ‘indian’ } then which one of the following is set P in listing form?
(A) {i, n, d}
(B) {i, n, d, a}
(C) {i, n, d, i, a}
(D) {n, d, a}
Ans: Option (B) – {i, n, d, a}
(iv) If T = { 1, 2, 3, 4, 5 } and M = { 3, 4, 7, 8 } then T ∪ M = ?
(A) { 1, 2, 3, 4, 5, 7 }
(B) { 1, 2, 3, 7, 8 }
(C) { 1, 2, 3, 4, 5, 7, 8 }
(D) { 3, 4 }
Ans: Option (C) – { 1, 2, 3, 4, 5, 7, 8 }
(4) 70 trees were planted by Parth and 90 trees were planted by Pradnya on the occasion of Tree Plantation Week. Out of these; 25 trees were planted by both of them together. How many trees were planted by Parth or Pradnya?
Solution:
Let A be the set of saplings planted by Parth
∴ n(A) = 70
Let B be the set of saplings planted by Pradnya
∴ n(B) = 90
25 saplings are planted by both of them
∴ n(A ∩ B) = 25
Number of saplings planted either by Parth or Pradnya = n(A ∪ B) = ?
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
∴ n(A ∪ B) = 70 + 90 – 25
∴ n(A ∪ B) = 160 – 25
∴ n(A ∪ B) = 135
Ans: Number of saplings either planted by Parth or Pradnya are 135.
(4) 70 trees were planted by Parth and 90 trees were planted by Pradnya on the occasion of Tree Plantation Week. Out of these; 25 trees were planted by both of them together. How many trees were planted by Parth or Pradnya?
Solution:
Let A be the set of saplings planted by Parth
∴ n(A) = 70
Let B be the set of saplings planted by Pradnya
∴ n(B) = 90
25 saplings are planted by both of them
∴ n(A ∩ B) = 25
Number of saplings planted either by Parth or Pradnya = n(A ∪ B) = ?
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
∴ n(A ∪ B) = 70 + 90 – 25
∴ n(A ∪ B) = 160 – 25
∴ n(A ∪ B) = 135
Ans: Number of saplings either planted by Parth or Pradnya are 135.
(5) If n(A) = 20, n(B) = 28 and n(A ∪ B) = 36 then n(A ∩ B) = ?
Solution:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
∴ 36 = 20 + 28 – n(A ∩ B)
∴ 36 = 48 – n(A ∩ B)
∴ n(A ∩ B) = 48 – 36
∴ n(A ∩ B) = 12
Ans: n(A ∩ B) = 12
(6) In a class, 8 students out of 28 have a dog as their pet animal at home, 6 students have a cat as their pet animal. 10 students have a dog and a cat both, then how many students do not have a dog or cat as their pet at home?
Solution:
Let A be the set of students having a dog as a pet at home.
∴ n(A) = 8 + 10 = 18
Let B be the set of students having a cat as a pet at home.
∴ n(B) = 6 + 10 = 16
10 students have both a dog and a cat as pets at home.
∴ n(A ∩ B) = 10
Number of students having either dog or cat as pet = n(A ∪ B) = ?
We know that,
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
∴ n(A ∪ B) = 18 + 16 – 10
∴ n(A ∪ B) = 34 – 10
∴ n(A ∪ B) = 24
Number of students having either dog or cat as pet are 4.
Now,
Number of students do not have a dog or cat as pet = 28 – 24 = 4
Ans: 4 students do not have a dog or cat as pets.
(7) Represent the union of two sets by Venn diagram for each of the following.
(i) A = { 3, 4, 5, 7 }, B = { 1, 4, 8 }
Ans:
A ∪ B = { 1, 3, 4, 5, 7, 8 }
Venn Diagram:
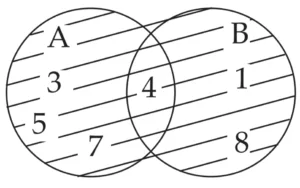
(ii) P = { a, b, c, e, f }, Q = { l, m, n, e, b }
Ans:
P ∪ Q = { a, b, c, e, f, l, m, n }
Venn Diagram:

(iii) X = { x | x is a prime number between 80 and 100 }
Y = { y | y is an odd number between 90 and 100 }
Solution:
X = { 83, 89, 97 }
Y = { 91, 93, 95, 97, 99 }
∴ X ∪ Y = { 83, 89, 91, 93, 95, 97, 99 }
Venn Diagram:

(8) Write the subset relations between the following sets.
X = set of all quadrilaterals.
Y = set of all rhombuses.
S = set of all squares.
T = set of all parallelograms.
V = set of all rectangles.
Ans:
Y ⊆ X
Y ⊆ T
S ⊆ X
S ⊆ Y
S ⊆ T
S ⊆ V
T ⊆ X
V ⊆ X
V ⊆ T
(9) If M is any set, then write M ∪ φ and M ∩ φ.
Solution:
M ∪ φ = M
M ∩ φ = φ
(10) Observe the Venn diagram and write the given sets U, A, B, A ∪ B, A ∩ B.
Ans:
U = { 1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13 }
A = { 1, 2, 3, 5, 7 }
B = { 1, 5, 8, 9, 10 }
A ∪ B = { 1, 2, 3, 5, 7, 8, 9, 10 }
A ∩ B = { 1, 5 }
(11) If n(A) = 7, n(B) = 13, n(A ∩ B) = 4 then n(A ∪ B) =?
Solution:
We know that,
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
∴ n(A ∪ B) = 7 + 13 – 14
∴ n(A ∪ B) = 20 – 4
∴ n(A ∪ B) = 16
Ans: n(A ∪ B) = 16
