Chapter 5 - Heat
1. Fill in the blanks and rewrite the sentence.
a. The amount of water vapour in air is determined in terms of its ______
Ans: The amount of water vapour in air is determined in terms of its absolute humidity.
b. If objects of equal masses are given equal heat, their final temperature will be different. This is due to difference in their ______
Ans: If objects of equal masses are given equal heat, their final temperature will be different. This is due to difference in their specific heat capacities.
c. During transformation of liquid phase to solid phase, the latent heat is ______
Ans: During transformation of liquid phase to solid phase, the latent heat is released.
2. Observe the following graph. Considering the change in volume of water as its temperature is raised from 0 ⁰C, discuss the difference in the behaviour of water and other substances. What is this behaviour of water called?
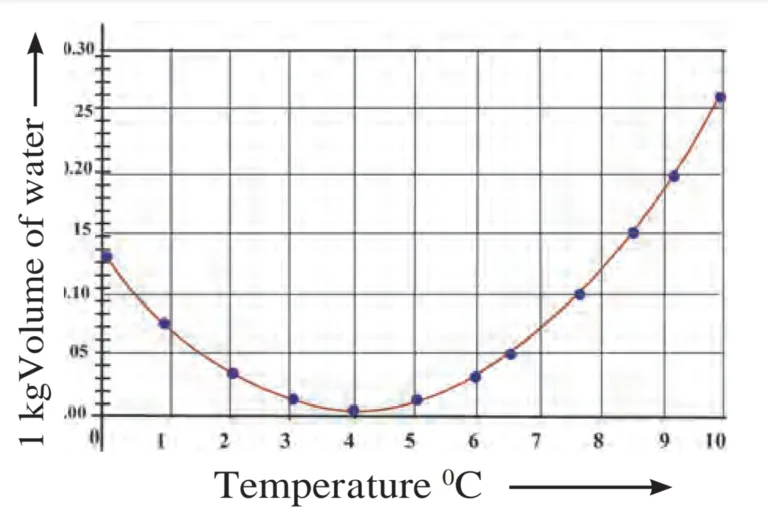
Ans:
(i) Liquids expand on heating and contract on cooling.
(ii) But water exhibits exceptional behaviour in the temperature range of 0 °C to 4 °C.
(iii) When water is heated from 0 °C up to 4 °C, instead of expanding, it contracts. Its volume decreases continuously from 0 °C to 4 °C.
(iv) At 4 °C, its volume is at its minimum.
(v) Upon heating further, however, it expands and its volume increases.
(vi) This behaviour of water between temperature intervals of 0 °C and 4 °C is called anomalous behaviour of water.
(vii) Phenomena observed due to the anomalous behaviour of water are:
a) Survival of aquatic life in cold regions,
b) Cracking of rocks in winter,
c) Breaking of pipes for water supply in cold regions.
3. What is meant by specific heat capacity? How will you prove experimentally that different substances have different specific heat capacities?
Ans: The amount of heat energy required to raise the temperature of a unit mass of an object by 1 °C is called the specific heat or specific heat capacity of that object.

Experimental verification:
(i) Solid spheres of iron, copper, and lead of equal mass are taken and placed into boiling water in the beaker till they attain a temperature of 100 °C.
(ii) These spheres are then immediately placed on the thick slab of wax simultaneously.
(iii) It is observed that each of the spheres reaches a different depth in the wax slab. The iron sphere goes deepest, followed by the copper and then the lead sphere.
(iv) The sphere that absorbs more heat from water supplies more heat to wax, causing more melting and going deeper in wax.
(v) This proves that for an equal rise in temperature, the three spheres have absorbed different amounts of heat and possess different specific heat capacities.
4. While deciding the unit for heat, which temperature interval is chosen? Why?
Ans: While deciding the unit for heat, the temperature interval chosen is 14.5 °C to 15.5 °C. The reason for this is that when 1 kg of water is heated to 1 °C in various temperature ranges, the amount of heat required to raise the temperature by 1 °C varies slightly from range to range. Hence, it is essential to define a specific temperature range while defining a unit of heat.
5. Explain the following temperature vs time graph.
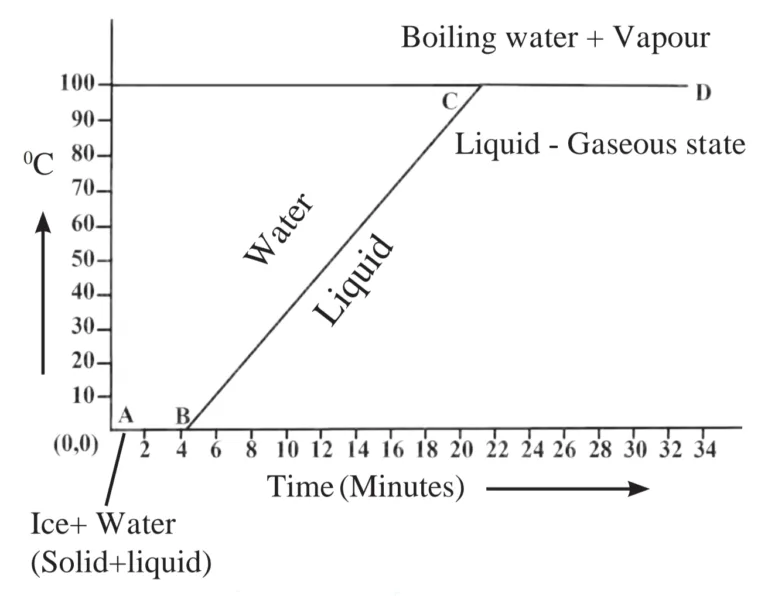
Ans:
(i) The given temperature v/s time graph demonstrates the behaviour of water when heated continuously and uniformly.
(ii) a. Line segment AB indicates the temperature of ice remaining constant at 0 °C for a certain period of time (about 4 minutes).
b. This means, the amount of heat (latent fusion) supplied to ice is entirely used for changing its state from solid to liquid.
c. Thus, line segment AB denotes the conversion of ice at 0°C into water at 0 °C.
(iii) Line segment BC indicates a continuous rise in the temperature of water from 0 °C to 100 °C.
(iv) a. At point C, the boiling point of water is reached, and heat energy (latent heat of vaporisation) supplied further is used to convert water into steam.
b. During this transformation, temperature remains unchanged, as represented by line segment CD.
c. Thus, line segment CD denotes the conversion of water at 100 °C into steam at 100 °C.
6. Explain the following:
a. What is the role of anomalous behaviour of water in preserving aquatic life in regions of cold climate?
Ans:
(i) In cold climates, the temperature of the water in ponds and lakes starts falling.
(ii) As it gets colder, water contracts. As a result, the density of water increases, and it goes down. To replace it, warmer water from below rises up. This process continues until the temperature of the water at the bottom of the pond reaches 4 °C.
(iii) Water, due to its anomalous behaviour, possesses maximum density at 4 °C.
(iv) If the temperature lowers further, ice is formed at the surface of the pond, with water below it.
(v) Ice, being a poor conductor of heat, blocks further heat exchange between the atmosphere and the water in the pond.
(vi) This maintains the temperature of water below the surface of ponds or lakes at 4 °C, enabling the survival of aquatic plants and animals.
b. How can you relate the formation of water droplets on the outer surface of a bottle taken out of the refrigerator with formation of dew?
Ans:
(i) When the temperature of the air at dawn falls, the air becomes saturated with vapour. As a result, the excess vapour condenses on the surface of objects in the form of dew.
(ii) When a bottle is taken out of the refrigerator, it cools the air surrounding it. Air in the vicinity becomes saturated with vapour and excess vapour condenses on the surface of the bottle in the form of water droplets.
(iii) Thus, both phenomena take place due to air reaching its dew point temperature.
c. In cold regions in winter, the rocks crack due to anomalous expansion of water.
Ans:
(i) When water is accumulated in a fissure in a rock, as the temperature in cold climates dips below 4 °C, it starts expanding instead of contracting.
(ii) Between temperature falls of 4 °C and 0 °C, the volume of water increases continuously due to the anomalous behaviour of water.
(iii) At the same time, rocks undergo contraction.
(iv) As a result, rocks experience force applied by water and crack.
7. Answer the following:
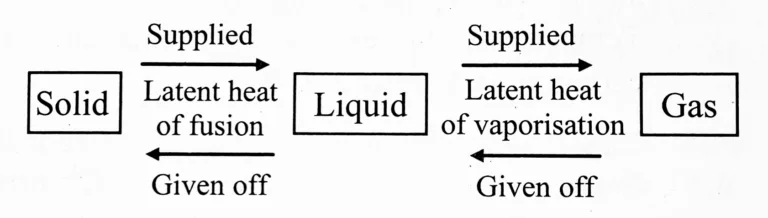
a. What is meant by latent heat? How will the state of matter transform if latent heat is given off?
Ans:
(i) The heat energy required to change a substance from one state to another at a constant temperature is called the latent heat of the substance.
(ii) When latent heat is given off, the bonding between atoms or molecules of a substance strengthens, causing transformation from one state to another, i.e., from gaseous state to liquid state or liquid state to solid state.
b. Which principle is used to measure the specific heat capacity of a substance?
Ans: The principle of heat exchange is used to measure the specific heat capacity of a substance.
c. Explain the role of latent heat in the change of state of a substance?
Ans:
(i) The heat energy required to change a substance from one state to another at a constant temperature is called the latent heat of the substance.
(ii) When latent heat is supplied to a substance, it is used to weaken the bonds between atoms or molecules of the substance.
(iii) When a solid substance is provided with latent heat of fusion, weakening of bonds results in distancing of atoms or molecules of the solid, and eventually it changes into a liquid state.
(iv) Similarly, when a liquid substance is provided with the latent heat of vaporisation, it changes into a gaseous state.
(v) Conversely, when latent heat is released or given off from a substance, it results in strengthening the bonds between atoms or molecules, causing a change in the substance’s state.
(vi) When a liquid substance gives off the latent heat of fusion, bonds between atoms or molecules grow stronger, bringing them closer, and eventually liquid changes into solid.
(vii) Similarly, when a gaseous substance gives off the latent heat of vaporisation, it changes into a liquid.
d. On what basis and how will you determine whether air is saturated with vapour or not?
Ans:
(i) When air is saturated with vapour, excess vapour condenses on the surface of objects in the form of water droplets.
(ii) The presence of water droplets affirms that the air is saturated with vapour.
8. Read the following paragraph and answer the questions.
If heat is exchanged between a hot and cold object, the temperature of the cold object goes on increasing due to gain of energy and the temperature of the hot object goes on decreasing due to loss of energy.
The change in temperature continues till the temperatures of both the objects attain the same value. In this process, the cold object gains heat energy and the hot object loses heat energy. If the system of both the objects is isolated from the environment by keeping it inside a heat resistant box (meaning that the energy exchange takes place between the two objects only), then no energy can flow from inside the box or come into the box.
(i) Heat is transferred from where to where?
Ans: Heat is transferred from hot objects to cold objects.
(ii) Which principle do we learn about from this process?
Ans: Principle of heat exchange.
(iii) How will you state the principle briefly?
Ans: As inside the heat resistant box, the heat lost by hot object exactly equals heat gained by cold object, principle of heat exchange is stated as: In an isolated system,
Heat lost by hot object = Heat gained by cold object.
(iv) Which property of the substance is measured using this principle?
Ans: Specific heat capacity of an object is measured using this principle.
9. Solve the following problems:
a. Equal heat is given to two objects A and B of mass 1 g. Temperature of A increases by 3 ⁰C and B by 5 ⁰C. Which object has more specific heat? And by what factor?
Given:
Q \(_{A}\) = Q\(_{B}\)
m\(_{A}\) = m\(_{B}\) = 1g
∆T\(_{A}\) = 3 ⁰C
∆T\(_{B}\) = 5 ⁰C
To find:
The object which has more specific heat and by what factor
Solution:
Heat absorbed by object A (Q\(_{A}\)) = m\(_{A}\) c\(_{A}\) ∆T\(_{A}\)
Heat absorbed by object B (Q\(_{B}\)) = m\(_{B}\) c\(_{B}\) ∆T\(_{B}\)
Now,
Q \(_{A}\) = Q\(_{B}\) …[Given]
∴ m\(_{A}\) c\(_{A}\) ∆T\(_{A}\) = m\(_{B}\) c\(_{B}\) ∆T\(_{B}\)
∴ 1 × c\(_{A}\) × 3 ⁰C = 1 × c\(_{B}\) × 5 ⁰C
∴ 3 c\(_{A}\) = 5 c\(_{B}\)
∴ c\(_{A}\) = \(\large \frac {5}{3}\) c\(_{B}\)
Ans: Object A has more specific heat than object B by factor of \(\large \frac {5}{3}\).
b. Liquid ammonia is used in ice factory for making ice from water. If water at 20 ⁰C is to be converted into 2 kg ice at 0 ⁰C, how many grams of ammonia are to be evaporated?
(Given: The latent heat of vaporization of ammonia= 341 cal/g)
Given:
Mass of water/ice (m) = 2 kg = 2 × 10³ g
Change in temperature of water (∆T) = 20 – 0 = 20 ⁰C
Latent heat of vaporisation of ammonia (L) = 341 cal/g
We know that:
Specific heat of water (\(c_{w}\)) = 1 cal/g ⁰C
Latent heat of melting of ice (L\(_{i}\)) = 80 cal/g
To find:
Mass of ammonia (M)
Solution:
Q\(_{1}\) (heat lost by water) = m c\(_{w}\) ∆T
∴ Q\(_{1}\) = 2 × 10³ g × 1 cal/g ⁰C × 20 ⁰C
∴ Q\(_{1}\) = 40 × 10³ cal
Q\(_{2}\) (heat absorbed by ammonia) = m L\(_{i}\)
∴ Q\(_{2}\) = 2 × 10³ g × 80 cal/g
∴ Q\(_{2}\) = 160 × 10³ cal
Total energy given off is,
Q = Q\(_{1}\) + Q\(_{2}\)
∴ Q = 40 × 10³ cal + 160 × 10³ cal
∴ Q = (40 + 160) 10³ cal
∴ Q = 200 × 10³ cal
According to the principle of heat exchange, this heat energy is to be taken away using ‘M’ mass of liquid ammonia.
∴ Q = M L
∴ 200 × 10³ cal = M × 341 cal/g
∴ M = \(\large \frac {200\, ×\, 10³}{341}\)
∴ M = 586.5 g
Ans: To convert 2 kg water at 20 ⁰C into ice at 0 ⁰C completely, 586.5 g of ammonia should be evaporated.
c. A thermally insulated pot has 150 g ice at temperature 0 ⁰C. How much steam of 100 ⁰C has to be mixed to it, so that water of temperature 50 ⁰C will be obtained?
(Given : latent heat of melting of ice = 80 cal/g, latent heat of vaporization of water = 540 cal/g, specific heat of water = 1 cal/g ⁰C)
Given:
m
c
t\(_{1}\)
t\(_{2}\)
L
Q\(_{A}\)
Steam
m\(_{1}\)
1 cal/g°C
100°C
50°C
540 cal/g
Q\(_{B}\)
Ice
150g
1 cal/g°C
0°C
50°C
80 cal/g
To find:
m\(_{1}\) = ?
Formulae:
Q\(_{A}\) = Q\(_{B}\)
Q = mc∆T
Q = mL
Solution:
(i) Steam
Steam (100°C) \(\xrightarrow{mL}\) Water (100°C) \(\xrightarrow{mc\triangle T}\) Water (50°C)
∴ Q\(_{A}\) = m\(_{1}\) L\(_{1}\) + m\(_{1}\) c\(_{1}\) ∆t\(_{1}\) …(i)
(ii) Ice
Ice (0°C) \(\xrightarrow{mL}\) Water (0°C) \(\xrightarrow{mc\triangle T}\) Water (50°C) ∴ Q\(_{B}\) = mL + mc∆T … (ii)
from (i) and (ii)
Q\(_{B}\) = Q\(_{A}\)
∴ mL + mc∆T = m\(_{1}\) L\(_{1}\) + m\(_{1}\) c\(_{1}\) ∆T
∴ (150 × 80) + {150 × 1 × (50 – 0)} = {m\(_{1}\) × 540} + {m\(_{1}\) × 1 × (100 – 50)}
∴ 12000 + 7500 = m\(_{1}\) (540 + 50)
∴ 19500 = m\(_{1}\) × 590
∴ m\(_{1}\) = \(\large \frac {19500}{590}\)
∴ m\(_{1}\) = 33.05 ~ 33
Ans: 33g steam has to be mixed.
d. A calorimeter has mass 100 g and specific heat 0.1 kcal/ kg ⁰C. It contains 250 gm of liquid at 30 ⁰C having specific heat of 0.4 kcal/kg ⁰C. If we drop a piece of ice of mass 10 g at 0 ⁰C, What will be the temperature of the mixture?
Given:
m
c
t\(_{1}\)
t\(_{2}\)
L
Q\(_{A}\)
Steam
80g
1 cal/g°C
97°C
0°C
540 cal/g
Q\(_{B}\)
Ice
m\(_{1}\)
1 cal/g°C
0°C
0°C
80 cal/g
To find:
m\(_{1}\) = ?
Formulae:
Q\(_{A}\) = Q\(_{B}\)
Q = mc∆T
Q = mL
Solution:
(i) Steam
Steam (97°C) \(\xrightarrow{mL}\) Water (97°C) \(\xrightarrow{mc\triangle T}\) Water (0°C)
∴ Q\(_{A}\) = m\(_{1}\) L\(_{1}\) + m\(_{1}\) c\(_{1}\) ∆t\(_{1}\)
∴ Q\(_{A}\) = (80 × 540) + {80 × 1 × (97 – 0)}
∴ Q\(_{A}\) = 43200 + 7760
∴ Q\(_{A}\) = 50960 cal …(i)
(ii) Ice
Ice (0°C) \(\xrightarrow{mL}\) Water (0°C)
∴ Q\(_{B}\) = m\(_{1}\)L\(_{1}\) … (ii)
from (i) and (ii),
Q\(_{A}\) = Q\(_{B}\)
∴ 50960 = m\(_{1}\) L\(_{1}\)
∴ 50960 = m\(_{1}\) × 80
∴ m\(_{1}\) = \(\large \frac {50960}{80}\)
∴ m\(_{1}\) = 637g
Ans: 637g of ice will melt and 50960 cal of heat energy is transferred to ice.
